Deel V – Coördinaten en Formele Analyse

5 Coördinatensystemen

5.1 Rechthoekig (Cartesiaans) Coördinatensysteem

Om onderscheid te maken tussen punten in de ruimte wordt een coördinatensysteem gecreëerd. De belangrijkste kenmerken van een coördinatensysteem zijn het oorsprongspunt en de coördinaatassen. Het oorsprongspunt kan gekozen worden op basis van wat het meest praktisch is, en voor de assen wordt meestal een Cartesiaans systeem gekozen omdat dit door zijn eenvoud wiskundig goed hanteerbaar is.

In een Cartesiaans coördinatensysteem:

• Staan de assen loodrecht (orthogonaal) op elkaar.
• Zijn de assen onafhankelijk van elkaar, d.w.z. het veranderen van de waarde van één coördinaat heeft geen invloed op de andere.
• Hebben de assen een richting en grootte en kunnen daarom als vectoren worden beschouwd.

Een punt in de ruimte wordt weergegeven door zijn coördinaten, bijvoorbeeld \( A(x_a, y_a) \). De \( x_a \) kan worden gevonden door een lijn te tekenen die parallel loopt aan de y-as; waar die lijn de x-as snijdt, ligt het punt \( x_a \). Hetzelfde geldt voor \( y_a \).

De afstand van punt A tot het oorsprongspunt kan worden gevonden met Pythagoras: \[ |A - O_{\text{oorsprong}}|^{2} = x_a^{2} + y_a^{2}. \]

Als we werken met een lijnstuk tussen A en B, dan is de lengte: \[ |A - B|^{2} = (x_a - x_b)^{2} + (y_a - y_b)^{2}. \]

Het voordeel hiervan is dat de lengte van het lijnstuk onafhankelijk is van het willekeurig gekozen oorsprongspunt; d.w.z. de waarden van \( x_a, y_a, x_b, y_b \) veranderen wel, maar het verschil \( |A - B| \), wat de lengte van het lijnstuk is, verandert niet.

5.2 Niet-Orthogonaal Coördinatensysteem

Om praktische redenen kan ook een coördinatensysteem worden gekozen waarvan de assen niet orthogonaal zijn. Ook in zo’n systeem kunnen we posities en afstanden beschrijven, maar de berekeningen worden iets complexer.

Een lijnstuk \( s \) in dit systeem is de som van de basisvectoren: \[ \vec{s} = x\,\vec{a} + y\,\vec{b}. \]

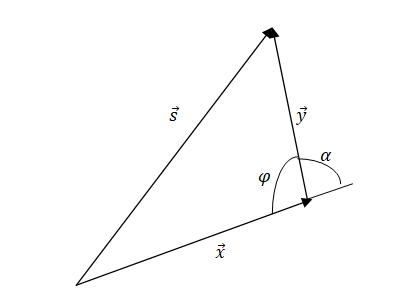
De grootte \( s \) van \( \vec{s} \) kan worden gevonden door het inproduct van \( \vec{s} \) met zichzelf: \[ \vec{s}\cdot\vec{s} = (x\vec{a} + y\vec{b}) \cdot (x\vec{a} + y\vec{b}) = x^{2}(\vec{a}\cdot\vec{a}) + xy(\vec{a}\cdot\vec{b}) + xy(\vec{b}\cdot\vec{a}) + y^{2}(\vec{b}\cdot\vec{b}). \]

Omdat \( \vec{a}\cdot\vec{a} = 1 \), \( \vec{b}\cdot\vec{b} = 1 \) en \( \vec{a}\cdot\vec{b} = \cos\alpha \), volgt: \[ s^{2} = x^{2} + 2xy\cos\alpha + y^{2}. \]

Als \( \varphi \) de hoek is tussen \( x \) en \( y \), dan is \[ \cos\alpha = -\cos\varphi, \qquad \cos\alpha = \cos(180^\circ - \varphi) = -\cos\varphi. \]

Dus: \[ s^{2} = x^{2} + y^{2} - 2xy\cos\varphi. \]

Dit is de bekende cosinusregel. Dus, naast de kwadraten van de coördinaten maakt ook het product van de coördinaten deel uit van de vergelijking.

5.3 Gekromde Coördinaten

In plaats van coördinaatassen die niet orthogonaal zijn, kan het ook praktisch zijn om gekromde coördinaten te gebruiken. Werken met deze coördinaten is uiteraard complexer, maar Einstein hanteerde de volgende benadering:

Een gekromde lijn kan worden beschouwd als een lijn opgebouwd uit oneindig kleine rechte lijnen. Door te kijken naar een oneindig klein gebied kunnen deze gekromde coördinaten worden beschouwd als een lokaal coördinatensysteem met rechte (lineaire) coördinaten, die echter niet per se rechthoekig zijn.

Omdat het coördinatensysteem hier oneindig kleine coördinaten betreft, worden de coördinaten aangeduid als \( dx, dy \) enzovoort. Bovendien hebben deze coördinaten coëfficiënten, en deze coëfficiënten bevatten informatie over de kromming van de coördinatensystemen. In het geval van kromming zijn deze coëfficiënten dus geen constante meer, maar parameters die afhankelijk zijn van hun locatie langs de coördinatensystemen.

Er wordt gezegd dat zwaartekracht de coördinatensystemen buigt en zo de ruimte‑tijd vervormt, wat een zwaartekrachtveld creëert en daardoor versnelling veroorzaakt. Door echter een gekromd coördinatensysteem zo te kiezen dat het zich beweegt en buigt in de richting van het zwaartekrachtsveld, wordt er geen kracht of zwaartekracht ervaren; op dezelfde manier als in de speciale relativiteitstheorie een bewegend coördinatensysteem werd gekozen om de snelheid van het bewegende object te neutraliseren.

5.4 Algemene Vorm voor een Coördinatensysteem

Laten we een vergelijking afleiden voor de relatie tussen een lijnsegment en zijn gebogen coördinatensysteem.

Om een meer algemene vorm (niet per se orthogonaal) te hebben, wordt aangenomen dat elke term een coëfficiënt \( g_{\mu\nu} \) heeft: \[ ds^{2} = g_{xx}\,dx\,dx + g_{xy}\,dx\,dy + g_{yx}\,dy\,dx + g_{yy}\,dy\,dy. \]

Hier, in het voorbeeld van de cosinusregel hierboven, is: \[ g_{xx} = g_{yy} = 1, \qquad g_{xy} = g_{yx} = -\cos\varphi. \]

De \( g_{\mu\nu} \) wordt de metrische tensor genoemd en kan, in dit tweedimensionale coördinatensysteem, worden beschouwd als een matrix met 2×2 elementen: \[ g_{\mu\nu} = \begin{pmatrix} 1 & -\cos\varphi \\ -\cos\varphi & 1 \end{pmatrix}. \]

5.5 De Metrische Tensor en Einstein‑Notatie

Voor een algemeen vierdimensionaal ruimte‑tijd‑stelsel (met tijd als coördinaat \( ct \)) is de metriek een 4×4‑tensor. De algemene vorm luidt: \[ ds^{2} = \sum_{\mu=0}^{3}\sum_{\nu=0}^{3} g_{\mu\nu}\,dx^{\mu}\,dx^{\nu} \]

In Einstein‑notatie: \[ ds^{2} = g_{\mu\nu}\,dx^{\mu}\,dx^{\nu}. \]

Hier lopen \( \mu \) en \( \nu \) van 0 tot 3, met coördinaten: \[ x^{0} = ct,\qquad x^{1} = x,\qquad x^{2} = y,\qquad x^{3} = z. \] De metrische tensor \( g_{\mu\nu} \) bevat alle informatie over de kromming van de ruimte‑tijd.

Voorbeeld van een metriek‑tensor in matrixvorm:

\[ g_{\mu\nu} = \begin{pmatrix} g_{00} & g_{01} & g_{02} & g_{03} \\ g_{10} & g_{11} & g_{12} & g_{13} \\ g_{20} & g_{21} & g_{22} & g_{23} \\ g_{30} & g_{31} & g_{32} & g_{33} \end{pmatrix}. \]

Als het coördinatenstelsel orthogonaal is, dan zijn alle kruistermen (waarbij \( \mu \neq \nu \)) nul: \[ g_{\mu\nu} = 0 \quad \text{voor } \mu \neq \nu. \]

De waarde van \( ds^{2} \) blijft onveranderd bij verandering van coördinatenstelsel, mits de bijhorende metriek correct aangepast wordt. Dat wil zeggen: \[ ds^{2} = g_{\mu\nu}(x)\,dx^{\mu}\,dx^{\nu} = g_{\alpha\beta}(y)\,dy^{\alpha}\,dy^{\beta}. \]

Hier zie je dat \( g_{\mu\nu} \) de “weegfactor” is die bepaalt hoe de infinitesimale verplaatsingen in de \( \mu \)- en \( \nu \)-richting bijdragen aan de lengte.

• De diagonaalelementen \( g_{\mu\mu} \) kun je zien als de “schaalfactoren” voor de bijbehorende coördinaatrichting.
• De niet‑diagonaalelementen \( g_{\mu\nu} \) met \( \mu \neq \nu \) beschrijven juist of de coördinaatrichtingen scheef staan (dus niet loodrecht zijn). In zekere zin zijn die verwant aan richtingscosinussen (projecties van de ene as op de andere).

Samenvattend

• Een coördinatensysteem is een hulpmiddel om de ruimte te structureren; afstanden kunnen daarin worden berekend.
• In orthogonale systemen geldt Pythagoras; in niet‑orthogonale systemen de cosinusregel.
• Gekromde coördinatenstelsels zijn nodig om zwaartekrachtsvelden in de algemene relativiteitstheorie te beschrijven.
• De metriek \( g_{\mu\nu} \) bevat alle informatie over afstandsbepaling en kromming van de ruimte of ruimte‑tijd.

5.6 Transformatie tussen twee Coördinatensystemen

Zoals eerder vermeld kan bij een gebogen coördinatensysteem “lokaal”, in een oneindig klein gebied, een coördinatensysteem met rechte lijnen worden gebruikt. Voor een vierdimensionaal coördinatensysteem heeft elke nieuwe coördinaat, in het nieuwe \( x \)-stelsel, een lineaire relatie met alle oude coördinaten in het oude \( y \)-stelsel, volgens: \[ dx^{0} = \frac{\partial x^{0}}{\partial y^{0}}\,dy^{0} + \frac{\partial x^{0}}{\partial y^{1}}\,dy^{1} + \frac{\partial x^{0}}{\partial y^{2}}\,dy^{2} + \frac{\partial x^{0}}{\partial y^{3}}\,dy^{3}. \]

Hetzelfde geldt voor de drie andere coördinaten, en dit leidt tot de algemene formule: \[ dx^{m} = \frac{\partial x^{m}}{\partial y^{r}}\,dy^{r}. \]

De sommatie gebeurt over de herhaalde index \( r \). Hierbij wordt impliciet gesommeerd over de index \( r \) volgens de Einstein‑notatie. Dit betekent dat voor elke waarde van \( m \), de afgeleiden over alle waarden van \( r \) (van 0 tot 3) worden opgeteld. Deze formule beschrijft hoe een infinitesimale verandering in het nieuwe coördinatenstelsel \( x^{m} \) wordt opgebouwd uit veranderingen in het oude stelsel \( y^{r} \).

5.6.1 Uitgebreide Toelichting op de Metrische Tensor

We beginnen met een Cartesiaans coördinatenstelsel, dat in dit geval vergelijkbaar is met de Minkowski‑vergelijking (zie hoofdstuk 5.10.1 en Appendix 9.1 vergelijking 11a) in de speciale relativiteitstheorie: \[ ds^{2} = c^{2}dt^{2} - dx^{2} - dy^{2} - dz^{2}. \]

Om de notatie compacter en algemener te maken, hernoemen we de differentiaaltermen: \[ cdt = dx^{0},\qquad dx = dx^{1},\qquad dy = dx^{2},\qquad dz = dx^{3}. \] Hierbij hebben alle differentiaaltermen de dimensie van lengte (meters).

In deze notatie wordt de ruimte‑tijdinterval geschreven als: \[ ds^{2} = (dx^{0})^{2} - (dx^{1})^{2} - (dx^{2})^{2} - (dx^{3})^{2} = \eta_{\mu\nu}\,dx^{\mu}\,dx^{\nu}. \]

De metrische tensor \( \eta_{\mu\nu} \) (de Minkowski‑metriek) is in matrixvorm: \[ \eta_{\mu\nu} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & -1 & -1 \end{pmatrix}. \]

Deze tensor beschrijft de afstandsstructuur van de vlakke ruimte‑tijd. De afstand tussen twee gebeurtenissen is dus: \[ ds^{2} = \eta_{\mu\nu}\,dx^{\mu}\,dx^{\nu}. \]

Nu beschouwen we een willekeurig coördinatenstelsel \( y^{\alpha} \), met coördinaten \( y^{0}, y^{1}, y^{2}, y^{3} \). De relatie tussen het oude en het nieuwe stelsel wordt gegeven door de kettingregel: \[ dx^{\mu} = \frac{\partial x^{\mu}}{\partial y^{0}}\,dy^{0} + \frac{\partial x^{\mu}}{\partial y^{1}}\,dy^{1} + \frac{\partial x^{\mu}}{\partial y^{2}}\,dy^{2} + \frac{\partial x^{\mu}}{\partial y^{3}}\,dy^{3}. \]

Of in compacte notatie: \[ dx^{\mu} = \frac{\partial x^{\mu}}{\partial y^{\alpha}}\,dy^{\alpha}, \qquad dx^{\nu} = \frac{\partial x^{\nu}}{\partial y^{\beta}}\,dy^{\beta}. \]

Substitutie in de Minkowski‑vorm: \[ ds^{2} = \eta_{\mu\nu}\,dx^{\mu}\,dx^{\nu} \] levert: \[ ds^{2} = \eta_{\mu\nu} \frac{\partial x^{\mu}}{\partial y^{\alpha}} \frac{\partial x^{\nu}}{\partial y^{\beta}} \,dy^{\alpha}\,dy^{\beta}. \]

We definiëren nu een nieuwe metrische tensor \( g_{\alpha\beta} \) in het coördinatenstelsel \( y^{\alpha} \), als volgt: \[ g_{\alpha\beta} = \eta_{\mu\nu} \frac{\partial x^{\mu}}{\partial y^{\alpha}} \frac{\partial x^{\nu}}{\partial y^{\beta}}. \]

Zodat: \[ ds^{2} = g_{\alpha\beta}\,dy^{\alpha}\,dy^{\beta}. \]

Gaan we vervolgens over naar een ander willekeurig coördinatenstelsel \( x^{\mu} \), dan geldt de inverse transformatie: \[ ds^{2} = g_{\alpha\beta} \frac{\partial y^{\alpha}}{\partial x^{\mu}} \frac{\partial y^{\beta}}{\partial x^{\nu}} \,dx^{\mu}\,dx^{\nu} = g_{\mu\nu}\,dx^{\mu}\,dx^{\nu}. \]

Hieruit volgt de algemene transformatieformule voor de metrische tensor: \[ g_{\mu\nu}(x) = \frac{\partial y^{\alpha}}{\partial x^{\mu}} \frac{\partial y^{\beta}}{\partial x^{\nu}} g_{\alpha\beta}(y). \] Deze formule beschrijft hoe de componenten van de metrische tensor transformeren onder een algemene coördinatentransformatie. Het is een fundamenteel resultaat in de algemene relativiteitstheorie en vormt de basis voor het begrip van gekromde ruimte‑tijd.

5.7 Transformatie tussen Cartesiaanse en Polaire (infinitesimale) Coördinaten

Als voorbeeld voeren we nu de transformatie uit van een Cartesiaans naar een sferisch (polair) coördinatenstelsel. We nemen aan dat de lezer bekend is met de standaardtransformatie tussen beide stelsels: \[ x = r\sin\theta\cos\varphi,\qquad y = r\sin\theta\sin\varphi,\qquad z = r\cos\theta. \]

Afleiding van \( dx, dy, dz \)

We differentiëren bovenstaande uitdrukkingen om de infinitesimale verplaatsingen te verkrijgen: \[ d\vec{x} = \begin{cases} dx = \sin\theta\cos\varphi\,dr + r\cos\theta\cos\varphi\,d\theta - r\sin\theta\sin\varphi\,d\varphi, \\[6pt] dy = \sin\theta\sin\varphi\,dr + r\cos\theta\sin\varphi\,d\theta + r\sin\theta\cos\varphi\,d\varphi, \\[6pt] dz = \cos\theta\,dr - r\sin\theta\,d\theta. \end{cases} \]

Deze vectoriële differentiëlen beschrijven de infinitesimale verplaatsingen in de x‑, y‑ en z‑richtingen in termen van \( dr, d\theta, d\varphi \).

Bepaling van het kwadraat van de differentiëlen

Om de grootte van \(dx\), \(dy\) en \(dz\) te bepalen, nemen we het inwendig product van elk van hen: \[ dx^{2} = dx \cdot dx,\qquad dy^{2} = dy \cdot dy,\qquad dz^{2} = dz \cdot dz. \]

Omdat de coördinaten \( r, \theta, \varphi \) loodrecht op elkaar staan, zijn de kruisproducten nul, wat resulteert in: \[ dx^{2} = \sin^{2}\theta\cos^{2}\varphi\,dr^{2} + r^{2}\cos^{2}\theta\cos^{2}\varphi\,d\theta^{2} + r^{2}\sin^{2}\theta\sin^{2}\varphi\,d\varphi^{2}, \] \[ dy^{2} = \sin^{2}\theta\sin^{2}\varphi\,dr^{2} + r^{2}\cos^{2}\theta\sin^{2}\varphi\,d\theta^{2} + r^{2}\sin^{2}\theta\cos^{2}\varphi\,d\varphi^{2}, \] \[ dz^{2} = \cos^{2}\theta\,dr^{2} + r^{2}\sin^{2}\theta\,d\theta^{2}. \]

Optelling van \(dx^{2} + dy^{2} + dz^{2}\)

Door de drie bovenstaande uitdrukkingen op te tellen, krijgen we: \[ dx^{2} + dy^{2} + dz^{2} = \sin^{2}\theta\cos^{2}\varphi\,dr^{2} + \sin^{2}\theta\sin^{2}\varphi\,dr^{2} + \cos^{2}\theta\,dr^{2} \] \[ \quad + r^{2}\cos^{2}\theta\cos^{2}\varphi\,d\theta^{2} + r^{2}\cos^{2}\theta\sin^{2}\varphi\,d\theta^{2} + r^{2}\sin^{2}\theta\,d\theta^{2} \] \[ \quad + r^{2}\sin^{2}\theta\sin^{2}\varphi\,d\varphi^{2} + r^{2}\sin^{2}\theta\cos^{2}\varphi\,d\varphi^{2}. \]

Gebruikmakend van de goniometrische identiteiten: \[ \cos^{2}\varphi + \sin^{2}\varphi = 1, \qquad \cos^{2}\theta + \sin^{2}\theta = 1, \] wordt dit vereenvoudigd tot: \[ dx^{2} + dy^{2} + dz^{2} = dr^{2} + r^{2}d\theta^{2} + r^{2}\sin^{2}\theta\,d\varphi^{2}. \tag{1} \]

Deze uitdrukking is precies de ruimtelijke component van de metriek in sferische coördinaten. De tijdcomponent kan toegevoegd worden als: \[ ds^{2} = c^{2}dt^{2} - dx^{2} - dy^{2} - dz^{2}, \] of in sferische vorm: \[ ds^{2} = c^{2}dt^{2} - dr^{2} - r^{2}d\theta^{2} - r^{2}\sin^{2}\theta\,d\varphi^{2}. \]

Volume-element in Sferische Coördinaten

Dit beschrijft de transformatie van een stelsel met Cartesiaanse coördinaten naar een stelsel met sferische (polaire) coördinaten.

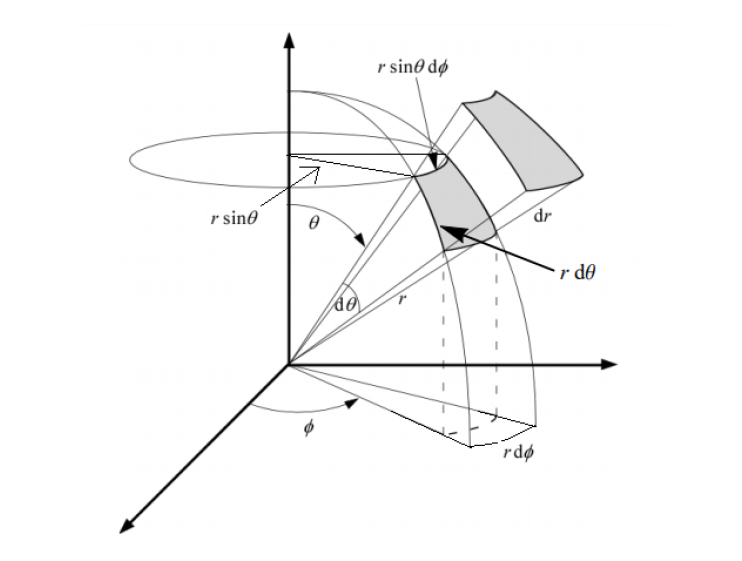
Volume‑element in Cartesische en Sferische Coördinaten

Het volume‑element in Cartesische coördinaten is: \[ dV = dx\,dy\,dz. \]

Na transformatie naar sferische coördinaten wordt dit: \[ dV = dr \cdot (r\,d\theta) \cdot (r\sin\theta\,d\varphi) = r^{2}\sin\theta\,dr\,d\theta\,d\varphi. \]

Berekening van het Volume van een Bol

Het totale volume van een bol met straal \( R \) volgt uit de integraal: \[ V =\iiint r^{2}\sin\theta\,dr\,d\theta\,d\varphi, \] met de integratiegrenzen:

• \( r \in [0, R] \)
• \( \theta \in [0, \pi] \)
• \( \varphi \in [0, 2\pi] \)

De integraal wordt dan: \[ V = \left( \int_{0}^{R} r^{2}\,dr \right) \left( \int_{0}^{\pi} \sin\theta\,d\theta \right) \left( \int_{0}^{2\pi} d\varphi \right). \]

Uitwerking: \[ \int_{0}^{R} r^{2}\,dr = \frac{1}{3}R^{3}, \qquad \int_{0}^{\pi} \sin\theta\,d\theta = [-\cos\theta]_{0}^{\pi} = 2, \qquad \int_{0}^{2\pi} d\varphi = 2\pi. \]

Dus: \[ V = \frac{1}{3}R^{3} \cdot 2 \cdot 2\pi = \frac{4}{3}\pi R^{3}. \]

Dit bevestigt het bekende resultaat voor het volume van een bol.

5.8 Oefening: Toepassen van de Metrische Transformatieformule

We laten hier zien hoe de metrische transformatieformule formeel wordt toegepast bij het overgaan van een Cartesisch naar een polair (sferisch) coördinatensysteem.

1. Algemene formules

We herinneren aan de volgende relaties:

1.1 Transformatie van coördinaten

\[ dx^{m} = \frac{\partial x^{m}}{\partial y^{r}}\,dy^{r}. \]

1.2 Lijnelement in Cartesiaanse coördinaten

\[ ds^{2} = \eta_{mn}\,d\xi^{m}\,d\xi^{n}. \]

1.3 Invariantie van het lijnelement onder coördinatentransformatie

\[ ds^{2} = g_{mn}(x)\,dx^{m}\,dx^{n} = g_{pq}(y)\,dy^{p}\,dy^{q}. \]

1.4 Transformatieformule voor de metriek

\[ g_{pq}(y) = g_{mn}(x)\, \frac{\partial x^{m}}{\partial y^{p}}\, \frac{\partial x^{n}}{\partial y^{q}}. \]

2. Van Cartesiaans naar Sferisch

We beschouwen de volgende Cartesiaanse metriek (in vierdimensionale ruimte‑tijd met signatuur \( (+,-,-,-) \)): \[ ds^{2} = c^{2}dt^{2} - dx^{2} - dy^{2} - dz^{2}. \]

De corresponderende vorm in sferische coördinaten is (met vergelijking 4.6.1): \[ ds^{2} = c^{2}dt^{2} - dr^{2} - r^{2}d\theta^{2} - r^{2}\sin^{2}\theta\,d\varphi^{2}. \]

Metriek in Cartesiaanse coördinaten

De metrische tensor in Cartesiaanse coördinaten is: \[ g_{\mu\nu} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}. \]

Hier is dus: \[ g_{00} = 1,\qquad g_{11} = -1,\qquad g_{22} = -1,\qquad g_{33} = -1, \] en alle overige elementen zijn nul.

Doelstelling

Vind de metriek \( g_{\mu\nu} \) in sferische coördinaten, namelijk: \[ g_{00} = 1,\qquad g_{11} = -1,\qquad g_{22} = -r^{2},\qquad g_{33} = -r^{2}\sin^{2}\theta. \]

3. Coördinatentransformatie

De sferische coördinaten worden uitgedrukt als functie van de Cartesiaanse coördinaten: \[ x = r\sin\theta\cos\varphi,\qquad y = r\sin\theta\sin\varphi,\qquad z = r\cos\theta. \]

We passen de transformatieformule toe: \[ dx^{m} = \frac{\partial x^{m}}{\partial y^{r}}\,dy^{r}. \]

Wanneer we deze formule volledig uitschrijven, dan ziet het er als volgt uit: \[ dt = \frac{\partial t}{\partial t}\,dt + \frac{\partial t}{\partial r}\,dr + \frac{\partial t}{\partial \theta}\,d\theta + \frac{\partial t}{\partial \varphi}\,d\varphi, \] \[ dx = \frac{\partial x}{\partial t}\,dt + \frac{\partial x}{\partial r}\,dr + \frac{\partial x}{\partial \theta}\,d\theta + \frac{\partial x}{\partial \varphi}\,d\varphi, \] \[ dy = \frac{\partial y}{\partial t}\,dt + \frac{\partial y}{\partial r}\,dr + \frac{\partial y}{\partial \theta}\,d\theta + \frac{\partial y}{\partial \varphi}\,d\varphi, \] \[ dz = \frac{\partial z}{\partial t}\,dt + \frac{\partial z}{\partial r}\,dr + \frac{\partial z}{\partial \theta}\,d\theta + \frac{\partial z}{\partial \varphi}\,d\varphi. \]

De differentiëlen worden

\[ dt = dt, \] \[ dx = \sin\theta\cos\varphi\,dr + r\cos\theta\cos\varphi\,d\theta - r\sin\theta\sin\varphi\,d\varphi, \] \[ dy = \sin\theta\sin\varphi\,dr + r\cos\theta\sin\varphi\,d\theta + r\sin\theta\cos\varphi\,d\varphi, \] \[ dz = \cos\theta\,dr - r\sin\theta\,d\theta. \]

Dus de elementen van de Jacobiaan zijn

\[ \frac{\partial t}{\partial t} = 1,\qquad \frac{\partial t}{\partial r} = 0,\qquad \frac{\partial t}{\partial \theta} = 0,\qquad \frac{\partial t}{\partial \varphi} = 0, \] \[ \frac{\partial x}{\partial t} = 0,\qquad \frac{\partial x}{\partial r} = \sin\theta\cos\varphi,\qquad \frac{\partial x}{\partial \theta} = r\cos\theta\cos\varphi,\qquad \frac{\partial x}{\partial \varphi} = -r\sin\theta\sin\varphi, \] \[ \frac{\partial y}{\partial t} = 0,\qquad \frac{\partial y}{\partial r} = \sin\theta\sin\varphi,\qquad \frac{\partial y}{\partial \theta} = r\cos\theta\sin\varphi,\qquad \frac{\partial y}{\partial \varphi} = r\sin\theta\cos\varphi, \] \[ \frac{\partial z}{\partial t} = 0,\qquad \frac{\partial z}{\partial r} = \cos\theta,\qquad \frac{\partial z}{\partial \theta} = -r\sin\theta,\qquad \frac{\partial z}{\partial \varphi} = 0. \]

4. Berekenen van de Nieuwe Metriek

We passen nu de transformatieformule toe: \[ g_{pq}(y) = g_{mn}(x)\, \frac{\partial x^{m}}{\partial y^{p}}\, \frac{\partial x^{n}}{\partial y^{q}}. \]

We werken nu de metrische tensorelementen uit. In volledige vorm: \[ g_{00}(y) = g_{00}(x)\frac{\partial x^{0}}{\partial y^{0}}\frac{\partial x^{0}}{\partial y^{0}} + g_{01}(x)\frac{\partial x^{0}}{\partial y^{0}}\frac{\partial x^{1}}{\partial y^{0}} + g_{02}(x)\frac{\partial x^{0}}{\partial y^{0}}\frac{\partial x^{2}}{\partial y^{0}} + g_{03}(x)\frac{\partial x^{0}}{\partial y^{0}}\frac{\partial x^{3}}{\partial y^{0}} \] \[ +\, g_{10}(x)\frac{\partial x^{1}}{\partial y^{0}}\frac{\partial x^{0}}{\partial y^{0}} + g_{11}(x)\frac{\partial x^{1}}{\partial y^{0}}\frac{\partial x^{1}}{\partial y^{0}} + g_{12}(x)\frac{\partial x^{1}}{\partial y^{0}}\frac{\partial x^{2}}{\partial y^{0}} + g_{13}(x)\frac{\partial x^{1}}{\partial y^{0}}\frac{\partial x^{3}}{\partial y^{0}} \] \[ +\, g_{20}(x)\frac{\partial x^{2}}{\partial y^{0}}\frac{\partial x^{0}}{\partial y^{0}} + g_{21}(x)\frac{\partial x^{2}}{\partial y^{0}}\frac{\partial x^{1}}{\partial y^{0}} + g_{22}(x)\frac{\partial x^{2}}{\partial y^{0}}\frac{\partial x^{2}}{\partial y^{0}} + g_{23}(x)\frac{\partial x^{2}}{\partial y^{0}}\frac{\partial x^{3}}{\partial y^{0}} \] \[ +\, g_{30}(x)\frac{\partial x^{3}}{\partial y^{0}}\frac{\partial x^{0}}{\partial y^{0}} + g_{31}(x)\frac{\partial x^{3}}{\partial y^{0}}\frac{\partial x^{1}}{\partial y^{0}} + g_{32}(x)\frac{\partial x^{3}}{\partial y^{0}}\frac{\partial x^{2}}{\partial y^{0}} + g_{33}(x)\frac{\partial x^{3}}{\partial y^{0}}\frac{\partial x^{3}}{\partial y^{0}}. \]

Voorbeeld: de radiale component \( g_{rr} \)

We vullen nu de juiste polaire en Cartesiaanse coördinaten in: \[ g_{rr} = g_{tt}\frac{\partial t}{\partial r}\frac{\partial t}{\partial r} + g_{xx}\frac{\partial x}{\partial r}\frac{\partial x}{\partial r} + g_{yy}\frac{\partial y}{\partial r}\frac{\partial y}{\partial r} + g_{zz}\frac{\partial z}{\partial r}\frac{\partial z}{\partial r}. \]

Omdat het Cartesiaanse systeem orthogonaal is, zijn alleen de elementen met gelijke indices niet nul: \[ g_{tt}=1,\qquad g_{xx}=-1,\qquad g_{yy}=-1,\qquad g_{zz}=-1. \]

De benodigde partiële afgeleiden zijn: \[ \frac{\partial t}{\partial r}=0, \qquad \frac{\partial x}{\partial r}=\sin\theta\cos\varphi, \qquad \frac{\partial y}{\partial r}=\sin\theta\sin\varphi, \qquad \frac{\partial z}{\partial r}=\cos\theta. \]

Dus: \[ g_{rr} = 1\cdot 0^{2} - (\sin\theta\cos\varphi)^{2} - (\sin\theta\sin\varphi)^{2} - (\cos\theta)^{2}. \]

Gebruikmakend van: \[ \cos^{2}\varphi + \sin^{2}\varphi = 1, \qquad \sin^{2}\theta + \cos^{2}\theta = 1, \] krijgen we: \[ g_{rr} = -\left[\sin^{2}\theta(\cos^{2}\varphi + \sin^{2}\varphi) + \cos^{2}\theta\right] = -(\sin^{2}\theta + \cos^{2}\theta) = -1. \]

Dus: \[ g_{rr} = -1. \]

1.5 Tijdcomponent

\[ g_{tt} = g_{tt}\left(\frac{\partial t}{\partial t}\right)^{2} + g_{xx}\left(\frac{\partial x}{\partial t}\right)^{2} + g_{yy}\left(\frac{\partial y}{\partial t}\right)^{2} + g_{zz}\left(\frac{\partial z}{\partial t}\right)^{2}. \]

Omdat: \[ \frac{\partial t}{\partial t}=1,\qquad \frac{\partial x}{\partial t}=0,\qquad \frac{\partial y}{\partial t}=0,\qquad \frac{\partial z}{\partial t}=0, \] volgt: \[ g_{tt} = 1. \]

1.6 Radiale component

\[ g_{rr} = g_{tt}\left(\frac{\partial t}{\partial r}\right)^{2} + g_{xx}\left(\frac{\partial x}{\partial r}\right)^{2} + g_{yy}\left(\frac{\partial y}{\partial r}\right)^{2} + g_{zz}\left(\frac{\partial z}{\partial r}\right)^{2} = -1. \]

Voor de radiale component vinden we: \[ g_{rr} = 0 - (\sin\theta\cos\varphi)^{2} - (\sin\theta\sin\varphi)^{2} - (\cos\theta)^{2}. \]

Gebruikmakend van: \[ \cos^{2}\varphi + \sin^{2}\varphi = 1, \qquad \sin^{2}\theta + \cos^{2}\theta = 1, \] krijgen we: \[ g_{rr} = -\left[\sin^{2}\theta(\cos^{2}\varphi + \sin^{2}\varphi) + \cos^{2}\theta\right] = -1. \]

1.7 Hoekcomponent \( \theta \)

\[ g_{\theta\theta} = g_{tt}\left(\frac{\partial t}{\partial \theta}\right)^{2} + g_{xx}\left(\frac{\partial x}{\partial \theta}\right)^{2} + g_{yy}\left(\frac{\partial y}{\partial \theta}\right)^{2} + g_{zz}\left(\frac{\partial z}{\partial \theta}\right)^{2}. \]

Met: \[ \frac{\partial x}{\partial \theta} = r\cos\theta\cos\varphi,\qquad \frac{\partial y}{\partial \theta} = r\cos\theta\sin\varphi,\qquad \frac{\partial z}{\partial \theta} = -r\sin\theta, \] volgt: \[ g_{\theta\theta} = -\left[ (r\cos\theta\cos\varphi)^{2} + (r\cos\theta\sin\varphi)^{2} + (-r\sin\theta)^{2} \right]. \]

\[ g_{\theta\theta} = -r^{2}\left[\cos^{2}\theta(\cos^{2}\varphi + \sin^{2}\varphi) + \sin^{2}\theta\right] = -r^{2}. \]

1.8 Hoekcomponent \( \varphi \)

\[ g_{\varphi\varphi} = g_{tt}\left(\frac{\partial t}{\partial \varphi}\right)^{2} + g_{xx}\left(\frac{\partial x}{\partial \varphi}\right)^{2} + g_{yy}\left(\frac{\partial y}{\partial \varphi}\right)^{2} + g_{zz}\left(\frac{\partial z}{\partial \varphi}\right)^{2}. \]

Met: \[ \frac{\partial x}{\partial \varphi} = -r\sin\theta\sin\varphi,\qquad \frac{\partial y}{\partial \varphi} = r\sin\theta\cos\varphi,\qquad \frac{\partial z}{\partial \varphi} = 0, \] volgt: \[ g_{\varphi\varphi} = -\left[ (-r\sin\theta\sin\varphi)^{2} + (r\sin\theta\cos\varphi)^{2} \right]. \]

\[ g_{\varphi\varphi} = -r^{2}\sin^{2}\theta(\sin^{2}\varphi + \cos^{2}\varphi) = -r^{2}\sin^{2}\theta. \]

Resultaat

De transformatie van een Cartesiaanse naar een sferische metrische tensor levert: \[ g_{tt} = 1,\qquad g_{rr} = -1,\qquad g_{\theta\theta} = -r^{2},\qquad g_{\varphi\varphi} = -r^{2}\sin^{2}\theta. \]

In matrixvorm: \[ g_{\mu\nu} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -r^{2} & 0 \\ 0 & 0 & 0 & -r^{2}\sin^{2}\theta \end{pmatrix}. \]

Dit komt overeen met de metriek van een polair coördinatensysteem in een driedimensionale ruimte.

Conclusie

De toepassing van de metrische transformatieformule op de overgang van Cartesiaanse naar sferische coördinaten leidt tot de verwachte sferische vorm van de ruimte‑tijd‑metriek. Deze oefening illustreert hoe tensortransformaties de coördinaat‑invariantie van fysische wetten garanderen binnen de algemene relativiteitstheorie.

5.9 Verdere Overwegingen over Co‑ en Contravariante Transformaties

5.9.1 Inleiding

In deze sectie onderzoeken we hoe basisvectoren en vectorcomponenten transformeren onder een coördinatentransformatie. We bekijken zowel de directe als de inverse transformatie en controleren hun consistentie. Deze overwegingen vormen de basis voor het begrip van covariante en contravariante objecten in de tensoranalyse.

5.9.2 Covariante Transformatie van Basisvectoren en Duale Vectoren (één‑vormen)

Beschouw een tweedimensionale vectorruimte met oorspronkelijke basisvectoren \( e_{1} \) en \( e_{2} \), die getransformeerd worden naar een nieuw coördinatenstelsel met basisvectoren \( e_{1}' \) en \( e_{2}' \). Deze transformatie is lineair en kan geschreven worden als: \[ e_{1}' = a_{11} e_{1} + a_{12} e_{2}, \qquad e_{2}' = a_{21} e_{1} + a_{22} e_{2}. \]

In matrixvorm: \[ \begin{pmatrix} e_{1}' \\ e_{2}' \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} e_{1} \\ e_{2} \end{pmatrix}. \]

Of korter: \[ e' = A\,e. \]

5.9.2.1 Inverse Transformatie van de Basisvectoren

Om de inverse transformatie (van het getransformeerde naar het oorspronkelijke systeem) te vinden, lossen we \( e_{1} \) en \( e_{2} \) op in termen van \( e_{1}' \) en \( e_{2}' \).

Stap 1: Lineaire combinatie opstellen

We nemen combinaties van de oorspronkelijke transformaties om \( e_{1} \) te isoleren: \[ a_{22} e_{1}' = a_{11} a_{22} e_{1} + a_{12} a_{22} e_{2}, \] \[ a_{12} e_{2}' = a_{12} a_{21} e_{1} + a_{12} a_{22} e_{2}. \]

Aftrekken geeft: \[ a_{22} e_{1}' - a_{12} e_{2}' = (a_{11} a_{22} - a_{12} a_{21})\, e_{1}. \]

Dus: \[ e_{1} = \frac{a_{22} e_{1}' - a_{12} e_{2}'}{a_{11} a_{22} - a_{12} a_{21}}. \]

Uit stap 1 vonden we: \[ e_{1} = \frac{a_{22} e_{1}' - a_{12} e_{2}'}{a_{11}a_{22} - a_{12}a_{21}}. \]

Stap 2: Idem voor \( e_{2} \)

Op analoge wijze vinden we: \[ a_{21} e_{1}' = a_{11}a_{21} e_{1} + a_{12}a_{21} e_{2}, \] \[ a_{11} e_{2}' = a_{11}a_{21} e_{1} + a_{11}a_{22} e_{2}. \]

Nu vermenigvuldigen we de eerste vergelijking met \(a_{22}\) en de tweede met \(a_{12}\), en trekken deze van elkaar af: \[ a_{21} e_{1}' - a_{11} e_{2}' = (a_{12}a_{21} - a_{11}a_{22})\, e_{2}. \]

Dus: \[ e_{2} = \frac{-a_{21} e_{1}' + a_{11} e_{2}'}{a_{11}a_{22} - a_{12}a_{21}}. \]

Inverse transformatie in matrixvorm

\[ \begin{pmatrix} e_{1} \\ e_{2} \end{pmatrix} = \frac{1}{a_{11}a_{22} - a_{12}a_{21}} \begin{pmatrix} a_{22} & -a_{12} \\ -a_{21} & a_{11} \end{pmatrix} \begin{pmatrix} e_{1}' \\ e_{2}' \end{pmatrix}. \]

Of korter: \[ e = A^{-1} e'. \]

5.9.2.2 Controle van de Inverse Transformatie

We controleren of \(A^{-1}A = I\).

De oorspronkelijke transformatie: \[ \begin{pmatrix} e_{1}' \\ e_{2}' \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} e_{1} \\ e_{2} \end{pmatrix}. \]

Nu vermenigvuldigen we \(A^{-1}\) met \(A\): \[ A^{-1}A = \frac{1}{a_{11}a_{22} - a_{12}a_{21}} \begin{pmatrix} a_{22} & -a_{12} \\ -a_{21} & a_{11} \end{pmatrix} \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}. \]

Uitwerking van het product: \[ \frac{1}{\det A} \begin{pmatrix} a_{22}a_{11} - a_{12}a_{21} & a_{22}a_{12} - a_{12}a_{22} \\ -a_{21}a_{11} + a_{11}a_{21} & -a_{21}a_{12} + a_{11}a_{22} \end{pmatrix} = \frac{1}{\det A} \begin{pmatrix} \det A & 0 \\ 0 & \det A \end{pmatrix}. \]

Dus: \[ A^{-1}A = I. \]

\[ \frac{a_{22}a_{11} - a_{21}a_{12}}{a_{11}a_{22} - a_{12}a_{21}} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}. \]

Dit vereenvoudigt tot de eenheidsmatrix: \[ I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}. \]

Dus: \[ A^{-1}A = I. \] De inverse transformatie is correct. Q.E.D.

5.9.2.3 Conclusie

We hebben de covariante transformatie voor basisvectoren en de inverse ervan afgeleid in een tweedimensionale ruimte. We hebben gecontroleerd dat de transformatie en de inverse elkaar opheffen tot de eenheidsmatrix, wat de consistentie van de transformatie tussen basisvectoren in verschillende coördinatensystemen bevestigt. Deze formele consistentie is essentieel voor het correct toepassen van tensortransformaties in de algemene relativiteitstheorie.

5.9.3 Contravariante Transformatie van Vectorcomponenten

In de differentiaalmeetkunde is het essentieel om onderscheid te maken tussen hoe basisvectoren (covariant) en hoe de componenten van vectoren (contravariant) transformeren onder een coördinatentransformatie. In deze sectie bekijken we de transformatie‑eigenschappen van contravariante vectorcomponenten in een tweedimensionale ruimte.

Vectorinvariantie en Componenttransformatie

Een vector \(V\) blijft geometrisch gezien hetzelfde onder een coördinatentransformatie, maar zijn componenten veranderen. In het oorspronkelijke coördinatensysteem schrijven we: \[ V = V^{1} e_{1} + V^{2} e_{2}, \] en in het nieuwe (getransformeerde) systeem: \[ V = V^{1'} e_{1}' + V^{2'} e_{2}'. \]

Aangezien de vector zelf invariant blijft, moeten de componenten \(V^{i}\) veranderen wanneer de basisvectoren veranderen.

Basisverandering

De nieuwe basisvectoren zijn lineair gerelateerd aan de oorspronkelijke basisvectoren via een matrix \(A\): \[ \begin{pmatrix} e_{1}' \\ e_{2}' \end{pmatrix} = A \begin{pmatrix} e_{1} \\ e_{2} \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} e_{1} \\ e_{2} \end{pmatrix}. \]

De basisverandering wordt gegeven door: \[ \begin{pmatrix} e_{1}' \\ e_{2}' \end{pmatrix} = A \begin{pmatrix} e_{1} \\ e_{2} \end{pmatrix}, \qquad A = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}. \]

De inverse transformatie voor de basisvectoren is dan: \[ \begin{pmatrix} e_{1} \\ e_{2} \end{pmatrix} = A^{-1} \begin{pmatrix} e_{1}' \\ e_{2}' \end{pmatrix}. \]

Afleiding van de Contravariante Transformatie

We drukken de basisvectoren \(e_{1}\) en \(e_{2}\) uit in termen van \(e_{1}'\) en \(e_{2}'\): \[ V = V^{1} e_{1} + V^{2} e_{2}. \]

Met de inverse transformatie: \[ e_{1} = \frac{a_{22} e_{1}' - a_{12} e_{2}'}{\det A}, \qquad e_{2} = \frac{-a_{21} e_{1}' + a_{11} e_{2}'}{\det A}, \] waar \[ \det A = a_{11}a_{22} - a_{12}a_{21}. \]

Invullen in de vector: \[ V = V^{1}\frac{a_{22} e_{1}' - a_{12} e_{2}'}{\det A} + V^{2}\frac{-a_{21} e_{1}' + a_{11} e_{2}'}{\det A}. \]

Herschrijven: \[ V = \frac{(a_{22}V^{1} - a_{21}V^{2})\,e_{1}' + (-a_{12}V^{1} + a_{11}V^{2})\,e_{2}'} {\det A}. \]

Maar we weten ook dat: \[ V = V^{1'} e_{1}' + V^{2'} e_{2}'. \]

Dus de componenttransformaties zijn: \[ V^{1'} = \frac{a_{22}V^{1} - a_{21}V^{2}}{\det A}, \qquad V^{2'} = \frac{-a_{12}V^{1} + a_{11}V^{2}}{\det A}. \]

Matrixvorm

\[ \begin{pmatrix} V^{1'} \\ V^{2'} \end{pmatrix} = \frac{1}{\det A} \begin{pmatrix} a_{22} & -a_{21} \\ -a_{12} & a_{11} \end{pmatrix} \begin{pmatrix} V^{1} \\ V^{2} \end{pmatrix}. \]

Dus: \[ V' = (A^{-1})^{T} V. \]

Inverse Transformatie van de Componenten

We beginnen met de getransformeerde vectorcomponenten: \[ V = V^{1'} e_{1}' + V^{2'} e_{2}'. \]

Met de directe transformatie van de basisvectoren: \[ e_{1}' = a_{11} e_{1} + a_{12} e_{2}, \qquad e_{2}' = a_{21} e_{1} + a_{22} e_{2}, \] krijgen we: \[ V = V^{1'}(a_{11} e_{1} + a_{12} e_{2}) + V^{2'}(a_{21} e_{1} + a_{22} e_{2}). \]

Dit geeft: \[ V = (a_{11}V^{1'} + a_{21}V^{2'})\,e_{1} + (a_{12}V^{1'} + a_{22}V^{2'})\,e_{2}. \]

Maar we weten ook dat: \[ V = V^{1} e_{1} + V^{2} e_{2}. \]

Daaruit volgen de relaties voor de oorspronkelijke vectorcomponenten: \[ V^{1} = a_{11}V^{1'} + a_{21}V^{2'}, \qquad V^{2} = a_{12}V^{1'} + a_{22}V^{2'}. \]

Matrixvorm

\[ \begin{pmatrix} V^{1} \\ V^{2} \end{pmatrix} = \begin{pmatrix} a_{11} & a_{21} \\ a_{12} & a_{22} \end{pmatrix} \begin{pmatrix} V^{1'} \\ V^{2'} \end{pmatrix}. \]

De basisvectoren transformeren volgens: \[ \begin{pmatrix} e_{1}' \\ e_{2}' \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} e_{1} \\ e_{2} \end{pmatrix}. \]

Daarentegen transformeren de vectorcomponenten in de tegengestelde richting: \[ \begin{pmatrix} V^{1'} \\ V^{2'} \end{pmatrix} = \frac{1}{a_{11}a_{22} - a_{12}a_{21}} \begin{pmatrix} a_{22} & -a_{21} \\ -a_{12} & a_{11} \end{pmatrix} \begin{pmatrix} V^{1} \\ V^{2} \end{pmatrix}. \]

5.9.4 Samenvatting van de Transformaties

De kernrelaties zijn als volgt:

1.9 Basisvectoren (covariant)

\[ e' = A\,e, \qquad e = A^{-1} e'. \]

1.10 Vectorcomponenten (contravariant)

\[ V' = (A^{-1})^{T} V, \qquad V = A^{T} V'. \]

Dus als de basisvectoren (covariante objecten) transformeren met: \[ e' = A e, \] dan transformeren de vectorcomponenten (contravariante objecten) met: \[ V' = (A^{-1})^{T} V. \]

\[ A = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}. \]

Terwijl de relatie tussen de componenten \(\begin{pmatrix}V^{1} \\ V^{2}\end{pmatrix}\) en \(\begin{pmatrix}V^{1'} \\ V^{2'}\end{pmatrix}\) wordt gegeven door de getransponeerde matrix: \[ A^{T} = \begin{pmatrix} a_{11} & a_{21} \\ a_{12} & a_{22} \end{pmatrix}. \]

De contravariante vectorcomponenten transformeren volgens: \[ \begin{pmatrix} V^{1'} \\ V^{2'} \end{pmatrix} = \frac{1}{a_{11}a_{22} - a_{12}a_{21}} \begin{pmatrix} a_{22} & -a_{21} \\ -a_{12} & a_{11} \end{pmatrix} \begin{pmatrix} V^{1} \\ V^{2} \end{pmatrix} = (A^{-1})^{T} V. \]

Dit is de inverse matrix en zijn getransponeerde.

Conclusie

Wanneer het coördinatensysteem verandert, transformeren de basisvectoren volgens een matrix \(A\), terwijl de vectorcomponenten transformeren met de inverse getransponeerde \((A^{-1})^{T}\). Deze contravariante transformatie zorgt ervoor dat de vector \(V\) zelf invariant blijft: zijn representatie past zich aan de veranderende basis aan, zodat de meetkundige betekenis behouden blijft.

5.10 Overwegingen over de Minkowski‑ en Schwarzschild‑Formules

5.10.1 Minkowski‑ruimte

De Minkowski‑metriek wordt gebruikt binnen de speciale relativiteitstheorie, waarin de effecten van zwaartekracht en versnelling worden verwaarloosd. In deze context bewegen referentiestelsels uniform met constante snelheid ten opzichte van elkaar, en het gebruikte coördinatenstelsel is lineair en vlak.

Beschouw een punt \(K\) in de ruimte‑tijd met een eigen coördinatensysteem. In dit systeem bevindt \(K\) zich voortdurend in de oorsprong, zodat enkel de tijd voortschrijdt. De afstand in ruimte‑tijd — het interval — is dan gegeven door: \[ s = c\,\tau, \] waar \(\tau\) de eigen‑tijd is.

waarbij \( \tau \) de eigen tijd is, gemeten door een klok die meebeweegt met \(K\). Een waarnemer bevindt zich elders in de ruimte‑tijd met een ander inertiaalstelsel, dat relatief beweegt ten opzichte van \(K\). Indien de waarnemer waarneemt dat \(K\) zich in de ruimte verplaatst, dan is de gemeten snelheid van \(K\): \[ v^{2} = \frac{x^{2} + y^{2} + z^{2}}{t^{2}}. \]

De Minkowski‑metriek in vierdimensionale ruimte‑tijd wordt dan geschreven als: \[ s^{2} = c^{2}t^{2} - x^{2} - y^{2} - z^{2}. \]

Voor een infinitesimaal segment langs een wereldlijn geldt: \[ ds^{2} = c^{2}dt^{2} - dx^{2} - dy^{2} - dz^{2}. \] Dit differentiaalsegment is als het ware een raaklijn aan de wereldlijn in ruimte‑tijd. Ook als de wereldlijn gekromd is (zoals bij versnelling of in aanwezigheid van zwaartekracht), kunnen we haar lokaal benaderen als opgebouwd uit lineaire segmenten.

De coördinaten \(t, x, y, z\) vertegenwoordigen vier componenten van een ruimte‑tijdvector. In een orthogonaal coördinatenstelsel (zoals in de Minkowski‑ruimte) kan het interval worden berekend via een gegeneraliseerde Pythagoras‑stelling. Indien we de tijdscomponent als imaginair nemen \(ict\), en de ruimtecomponenten als reëel, dan volgt de bekende Minkowski‑vorm.

Algemene structuur van het interval

We moeten beseffen dat \(t, x, y, z\) een grootte en richting hebben; het zijn vectoren. Het vinden van de grootte van \(s\) betekent het optellen van de vier vectoren. Als dit coördinatensysteem een orthogonaal systeem is, kan de stelling van Pythagoras worden toegepast op het ruimtedeel. Als we het tijdsdeel beschouwen als complex \(ic\,dt\), en voor de linkerkant \(ds = ic\,d\tau\), dan krijgen we door de coördinaten te kwadrateren de Minkowski‑formule.

In twee dimensies kunnen we schrijven: \[ s = a_{1}x_{1} + a_{2}x_{2}. \]

Om de grootte van \(s\) te vinden, berekenen we het inproduct van \(s\) met zichzelf: \[ s \cdot s = (a_{1}x_{1} + a_{2}x_{2}) \cdot (a_{1}x_{1} + a_{2}x_{2}), \] wat resulteert in: \[ s^{2} = a_{1}^{2}x_{1}^{2} + 2a_{1}a_{2}(x_{1}\cdot x_{2}) + a_{2}^{2}x_{2}^{2}. \]

Veralgemening naar vier dimensies

In vier dimensies veralgemeniseren we dit met behulp van de metrische tensor \(g_{\mu\nu}\): \[ s^{2} = \sum_{\mu,\nu} g_{\mu\nu}\,x^{\mu} x^{\nu} \]

Of in de notatie van Einstein (som over herhaalde indices): \[ s^{2} = g_{\mu\nu} x^{\mu} x^{\nu}. \]

Bij gebruik van een lokaal orthogonaal coördinatenstelsel verdwijnen alle producten waarbij \( \mu \neq \nu \). Als alleen een infinitesimaal klein lokaal gebied wordt beschouwd, wordt \(dx\) in plaats van \(x\) gebruikt, en hetzelfde geldt voor de overige coördinaten.

Ten slotte resulteert de vergelijking in een Minkowski‑ of Schwarzschild‑vorm: \[ ds^{2} = c^{2}(dx^{0})^{2} - (dx^{1})^{2} - (dx^{2})^{2} - (dx^{3})^{2}. \]

Algemeen: \[ ds^{2} = g_{00}\,c^{2}(dx^{0})^{2} + g_{11}(dx^{1})^{2} + g_{22}(dx^{2})^{2} + g_{33}(dx^{3})^{2}. \]

In de Minkowski‑ruimte zijn de componenten van de metrische tensor constant: \[ g_{00} = 1, \qquad g_{11} = g_{22} = g_{33} = -1. \]

Betekenis van de Minkowski‑formule

De Minkowski‑intervalformule luidt: \[ ds^{2} = c^{2}dt^{2} - dx^{2} - dy^{2} - dz^{2} = c^{2}dt'^{2} - dx'^{2} - dy'^{2} - dz'^{2}. \]

De linkerzijde representeert een object dat zich in zijn eigen (meebewegende) referentiestelsel bevindt: het ervaart uitsluitend een voortgang in eigen tijd \( \tau \).

Een waarnemer in het coördinatenstelsel \(t, x, y, z\) ziet het object bewegen met snelheid: \[ v^{2} = \frac{dx^{2} + dy^{2} + dz^{2}}{dt^{2}}. \]

Een tweede waarnemer in een ander inertiaalstelsel \(t', x', y', z'\) meet: \[ v'^{2} = \frac{dx'^{2} + dy'^{2} + dz'^{2}}{dt'^{2}}. \]

De relatie tussen eigen tijd \( \tau \) en coördinaattijd \(t\) wordt gegeven door: \[ ds^{2} = c^{2}dt^{2} - dx^{2} - dy^{2} - dz^{2} = c^{2}d\tau^{2}. \]

Dus: \[ c^{2}d\tau^{2} = c^{2}dt^{2}\left(1 - \frac{v^{2}}{c^{2}}\right) = c^{2}dt^{2}\,\gamma^{-2}. \]

Hier is \( \tau \) de zogenaamde eigen tijd, de tijd van een bewegende klok die zich in de oorsprong van zijn eigen meebewegende coördinatenstelsel bevindt.

De relatie tussen eigen tijd en waarnemerstijd is: \[ d\tau^{2} = \frac{dt^{2}}{\gamma^{2}}, \qquad dt = \gamma\,d\tau, \] waarbij de Lorentzfactor: \[ \gamma = \frac{1}{\sqrt{1 - v^{2}/c^{2}}}. \]

Omdat \( \gamma \ge 1 \), is \( d\tau \le dt \): een bewegende klok loopt langzamer dan een klok in rust vanuit het perspectief van een externe waarnemer.

5.10.2 Transformaties uitgevoerd door Schwarzschild

De Schwarzschild‑metriek vormt een uitbreiding van de Minkowski‑metriek doordat ze ook rekening houdt met de effecten van massa en zwaartekracht. In tegenstelling tot de vlakke ruimte‑tijd van de speciale relativiteitstheorie resulteert dit in een gekromde ruimte‑tijd. Deze kromming vertaalt zich in een niet‑lineair coördinatenstelsel, aangepast aan de sferische symmetrie rond een massief lichaam.

Van Cartesisch naar sferisch

Schwarzschild begint met de gebruikelijke vlakke (Cartesiaanse) coördinaten en voert een transformatie uit naar sferische coördinaten \(r, \theta, \varphi\). Dit resulteert in de volgende uitdrukking voor het ruimte‑tijd‑interval (in natuurlijke eenheden \(G=c=1\), maar hier behouden we \(c\) expliciet): \[ ds^{2} = \zeta^{2} c^{2} dt^{2} - \frac{dr^{2}}{\zeta^{2}} - r^{2} d\theta^{2} - r^{2}\sin^{2}\theta\, d\varphi^{2}, \] met: \[ \zeta^{2} = 1 - \frac{2GM}{rc^{2}}. \]

De determinant van de metriek

De determinant \(g\) van de metrische tensor blijkt in deze coördinaten: \[ g = \zeta^{2} \cdot \left(-\frac{1}{\zeta^{2}}\right) \cdot (-r^{2}) \cdot (-r^{2}\sin^{2}\theta) = -r^{4}\sin^{2}\theta. \]

Einstein had echter in zijn veldvergelijkingen graag dat in geschikte coördinaten \(g = -1\) zou gelden (zoals bij de Minkowski‑metriek). Schwarzschild onderzoekt daarom of er een coördinatentransformatie bestaat die deze voorwaarde oplevert.

Transformatie naar nieuwe coördinaten

(Volgende stap: hier kun je de Schwarzschild‑radiaaltransformatie invoeren, zoals \(R^{3} = r^{3} + \alpha^{3}\), of de isotrope coördinaten, afhankelijk van welke richting je verder wilt uitwerken.)

Om de determinant te normaliseren tot \( g = -1 \), definieert Schwarzschild nieuwe coördinaten \(x_{1}, x_{2}, x_{3}\), gebaseerd op: \[ \frac{dr}{dx_{1}} = \frac{1}{r^{2}}, \qquad \frac{d\theta}{dx_{2}} = \frac{1}{\sin\theta}, \qquad \frac{d\varphi}{dx_{3}} = 1. \]

Schwarzschild merkt op: “De nieuwe variabelen zijn de poolcoördinaten met determinant 1”. Om deze afgeleiden te verkrijgen, vindt hij de volgende relaties: \[ x_{1} = \frac{r^{3}}{3}, \qquad x_{2} = -\cos\theta, \qquad x_{3} = \varphi. \]

Deze nieuwe coördinaten transformeren de metriek tot: \[ ds^{2} = \zeta^{2} c^{2} dt^{2} - \frac{dx_{1}^{2}}{r^{4}\zeta^{2}} - r^{2}\cdot \frac{1}{\sin^{2}\theta}\,dx_{2}^{2} - r^{2}\sin^{2}\theta\,dx_{3}^{2}. \]

Substitutie van trigonometrische relaties

Omdat \(x_{2} = -\cos\theta\), geldt: \[ x_{2}^{2} = \cos^{2}\theta = 1 - \sin^{2}\theta \quad\Rightarrow\quad \sin^{2}\theta = 1 - x_{2}^{2}. \]

Daarmee herschrijven we de metriek als: \[ ds^{2} = \zeta^{2} c^{2} dt^{2} - \frac{dx_{1}^{2}}{r^{4}\zeta^{2}} - \frac{r^{2}}{1 - x_{2}^{2}}\,dx_{2}^{2} - r^{2}(1 - x_{2}^{2})\,dx_{3}^{2}. \]

De nieuwe metriekcomponenten

De componenten van de metrische tensor \(g_{\mu\nu}\) in deze getransformeerde coördinaten zijn nu: \[ g_{00} = \zeta^{2}, \qquad g_{11} = -\frac{1}{r^{4}\zeta^{2}}, \qquad g_{22} = -\frac{r^{2}}{1 - x_{2}^{2}}, \qquad g_{33} = -r^{2}(1 - x_{2}^{2}). \]

De determinant \(g\) van deze tensor is nu: \[ g = g_{00}\,g_{11}\,g_{22}\,g_{33} = -1. \]

Precies zoals gewenst. De transformatie die Schwarzschild uitvoerde is dus geldig en resulteert in een metriek met determinant \(-1\), ondanks de gekromde aard van de ruimte‑tijd.

Bijzondere gevallen

In het specifieke geval \( \theta = 90^\circ \) geldt \( \cos\theta = 0 \) en dus \( x_{2} = 0 \), wat leidt tot: \[ \sin^{2}\theta = 1 \quad\Longrightarrow\quad ds^{2} = \zeta^{2}c^{2}dt^{2} - \frac{dx_{1}^{2}}{r^{4}\zeta^{2}} - r^{2}dx_{2}^{2} - r^{2}dx_{3}^{2}. \]

In dit vlak rond het equatoriale vlak wordt de metriek nog eenvoudiger van vorm.

5.11 Schwarzschild’s: “On the Gravitational Field of a Mass Point According to Einstein’s Theory”

Het doel van Karl Schwarzschild in zijn artikel uit 1916 was het vinden van een exacte oplossing van de Einstein‑veldvergelijkingen in vacuüm. Deze oplossing beschrijft de ruimte‑tijd rond een massapunt dat langs een geodetische lijn beweegt in een vierdimensionale variëteit, waarbij het ruimte‑tijd‑interval \(ds\) centraal staat.

Voorwaarden voor de oplossing

De volgende voorwaarden worden aan de oplossing gesteld:

1. Tijdsonafhankelijkheid: Alle componenten van de metriek zijn onafhankelijk van de tijdscoördinaat \(x^{4}\).
2. Geen ruimte‑tijd‑koppeling: De gemengde componenten \(g_{\rho 4} = g_{4\rho} = 0\) voor \(\rho = 1,2,3\).
3. Sferische symmetrie: De oplossing is invariant onder orthogonale transformaties (rotaties) van \(x_{1}, x_{2}, x_{3}\); dit reflecteert sferische symmetrie.
4. Asymptotische vlakheid: Op oneindige afstand verdwijnen de componenten van de metrische tensor, met: \[ \lim_{r\to\infty} g_{44} = 1, \qquad \lim_{r\to\infty} g_{11} = g_{22} = g_{33} = -1. \]

Van Cartesiaanse naar bolcoördinaten

Schwarzschild begint met een algemene metriek in Cartesiaanse coördinaten: \[ ds^{2} = F\,dt^{2} - G\,(dx^{2} + dy^{2} + dz^{2}) - H\,(x\,dx + y\,dy + z\,dz)^{2}. \]

Vervolgens voert hij de standaardtransformaties naar bolcoördinaten uit: \[ x = r\sin\vartheta\cos\varphi,\qquad y = r\sin\vartheta\sin\varphi,\qquad z = r\cos\vartheta. \]

Na substitutie krijgen we voor het ruimte‑tijd‑interval in bolcoördinaten: \[ ds^{2} = F\,dt^{2} - G\,(dr^{2} + r^{2}d\vartheta^{2} + r^{2}\sin^{2}\vartheta\,d\varphi^{2}) - H\,r^{2}dr^{2}. \]

Dit wordt herschreven tot: \[ ds^{2} = F\,dt^{2} - \left(G + Hr^{2}\right)dr^{2} - G r^{2}\left(d\vartheta^{2} + \sin^{2}\vartheta\,d\varphi^{2}\right). \]

Transformatie naar determinant 1

Omdat de determinant van de metriek in dit geval niet gelijk is aan \(-1\), voert Schwarzschild een transformatie uit naar nieuwe variabelen waarmee deze voorwaarde wel vervuld wordt. Hij definieert: \[ x_{1} = \frac{r^{3}}{3}, \qquad x_{2} = -\cos\vartheta, \qquad x_{3} = \varphi. \]

Daarmee wordt het lijnsegment: \[ ds^{2} = F\,dt^{2} - \frac{G}{r^{4} + Hr^{2}}\,dx_{1}^{2} - \frac{G r^{2}}{1 - x_{2}^{2}}\,dx_{2}^{2} - r^{2}(1 - x_{2}^{2})\,dx_{3}^{2}. \]

De Schwarzschild‑oplossing

Door deze metriek in te vullen in de Einstein‑veldvergelijkingen en deze op te lossen in vacuum (\(T_{\mu\nu} = 0\)), vindt Schwarzschild de bekende oplossing: \[ ds^{2} = c^{2}d\tau^{2} = \left(1 - \frac{2GM}{c^{2}r}\right)c^{2}dt^{2} - \left(1 - \frac{2GM}{c^{2}r}\right)^{-1}dr^{2} - r^{2}d\theta^{2} - r^{2}\sin^{2}\theta\,d\varphi^{2}. \tag{12} \]

Deze vergelijking beschrijft de gekromde ruimte‑tijd rondom een sferisch symmetrisch massapunt in vacuüm. Hoewel Schwarzschild zijn afleiding begon met Cartesiaanse coördinaten, is de uiteindelijke oplossing handiger en inzichtelijker in bolcoördinaten, gezien de sferische symmetrie van het probleem.

Schwarzschild‑oplossing in Cartesiaanse coördinaten

Er bestaat ook een minder gebruikelijke vorm van de Schwarzschild‑oplossing in Cartesiaanse coördinaten, die als volgt luidt: \[ ds^{2} = c^{2}d\tau^{2} = \left(1 - \frac{2GM}{c^{2}r}\right)c^{2}dt^{2} - (dx^{2} + dy^{2} + dz^{2}) - \frac{2GM}{c^{2}r\left(1 - \frac{2GM}{c^{2}r}\right)} \left(\frac{x\,dx + y\,dy + z\,dz}{r}\right)^{2}. \tag{13} \]

Deze vorm is echter zelden praktisch, omdat bolcoördinaten veel beter passen bij de symmetrie van het probleem, bijvoorbeeld in toepassingen zoals de beschrijving van zwarte gaten of de buitenkant van sterren.

Bronnen

• K. Schwarzschild, On the Gravitational Field of a Point‑Mass, According to Einstein's Theory, 13 januari 1916.
• G. Oas, diverse besprekingen en analyses van de Schwarzschild‑oplossing. Zie ook het hoofdstuk Bibliografie aan het einde van dit document.

De Schwarzschild‑oplossing vormt een hoeksteen van de algemene relativiteitstheorie en wordt veelvuldig toegepast in de astrofysica bij de studie van zwarte gaten, neutronensterren en andere objecten met extreem sterke zwaartekrachtsvelden.