Deel IV – Experimenten en Verificaties
4 Experimenten ter bevestiging van Einsteins Theorie
In dit hoofdstuk bespreken we een reeks experimenten die de algemene relativiteitstheorie van Einstein empirisch ondersteunen. Een centraal hulpmiddel bij de analyse van deze experimenten is de Schwarzschild-oplossing van de Einstein-veldvergelijkingen.
De volgende experimenten komen aan bod:
- Het Hafele–Keating-experiment (zie hoofdstuk 4.1)
- De beweging van deeltjes in een zwaartekrachtsveld (zie hoofdstuk 4.2)
- De afbuiging van licht in de nabijheid van massa’s (zie hoofdstuk 4.3)
- De precessie van de periheliën van planeten, met name Mercurius (zie hoofdstuk 4.4)
- De Shapiro-tijdvertraging (zie hoofdstuk 4.5)
- De berekening van de baan van een kogel in een sterk zwaartekrachtsveld (zie hoofdstuk 4.8)
Deze experimenten vormen samen een krachtig bewijs voor de geldigheid van de algemene relativiteitstheorie. In elk geval biedt de Schwarzschild-metriek een wiskundig kader waarmee de waargenomen fenomenen nauwkeurig verklaard kunnen worden.
4.1 Experiment 1 – Het Hafele & Keating-Experiment met de Schwarzschild-Vergelijking
Afleiding gebaseerd op: A Hafele & Keating-like thought experiment, door Paul B. Andersen, 16 oktober 2008 (Andersen, 2008).
Het beroemde experiment van Hafele en Keating testte kwantitatieve voorspellingen van de relativiteitstheorie, met name de tijdsdilatatie als gevolg van zowel beweging (speciale relativiteitstheorie) als zwaartekracht (algemene relativiteitstheorie).
In dit experiment werden twee vliegtuigen uitgerust met cesiumklokken en liet men ze gelijktijdig in tegengestelde richtingen rond de aarde vliegen. Daarnaast bleef een derde cesiumklok op een vaste locatie op aarde (in Washington). De resultaten toonden aan dat de klokken aan boord verschillende tijdsdilatatie-effecten ondergingen, afhankelijk van hun bewegingsrichting en positie ten opzichte van de aarde.
De klok in het oostwaarts vliegende vliegtuig bewoog met de rotatie van de aarde mee. Daardoor had deze klok een grotere snelheid ten opzichte van het niet-roterende middelpunt van de aarde dan de grondklok. Dit leidde tot een sterkere tijdsdilatatie: de klok liep achter.
Daarentegen bewoog het westwaarts vliegende vliegtuig tegen de rotatie van de aarde in, wat resulteerde in een lagere snelheid ten opzichte van het aardcentrum, en dus in een zwakkere tijdsdilatatie: deze klok liep juist voor. Dit verschil in tijdsverloop toont aan dat de voortgang van de tijd afhankelijk is van de beweging van de waarnemer – een effect dat al in 1905 werd voorspeld door Einstein in zijn oorspronkelijke artikel over de speciale relativiteitstheorie.
Bron: (Crowell, 11 maart 2018)
Doel en Opzet
- Doel: Directe experimentele toets van Einsteins voorspellingen voor tijdsdilatatie door zowel beweging (speciale relativiteit) als zwaartekracht (algemene relativiteit).
- Opzet: Cesiumklokken werden in vliegtuigen oost- en westwaarts rond de aarde gevlogen, terwijl een referentieklok op aarde bleef. De tijdsverschillen tussen deze klokken werden gemeten en vergeleken met de theoretische voorspellingen.
Theoretisch Kader: Schwarzschild-metriek
De Schwarzschild-metriek beschrijft de ruimte-tijd buiten een sferisch symmetrisch massief lichaam zoals de aarde:
De Schwarzschild-metriek luidt:
\[ c^2 d\tau^2=\left(1-\frac{2GM}{ c^2r}\right) dt^2-\left(1-\frac{2GM}{ c^2r} \right)^{-1} dr^2-r^2 d\theta^2-r^2 \sin^2\theta \, d\phi^2 \tag{1} \]Hierbij geldt:
- t: de coördinatentijd, gemeten door een hypothetische klok buiten elk zwaartekrachtsveld;
- τ: de eigen tijd, gemeten door een meebewegende klok op positie r;
- r: afstand tot het middelpunt van de aarde;
- θ: breedtehoek ten opzichte van de Noordpool;
- ∅: lengtehoek ten opzichte van een vaste meridiaan;
- G: de gravitatieconstante;
- M: de massa van de aarde;
- c: de lichtsnelheid.
De Schwarzschild-metriek gebruikt een universeel (sferisch) coördinatenstelsel met als oorsprong het zwaartepunt van de aarde. De aarde roteert binnen dit coördinatenstelsel. Veranderingen in de hoeken θ en ∅ beschrijven beweging over het aardoppervlak.
Kleine veranderingen in tijd en ruimte worden respectievelijk aangeduid met dt, dr, dθ en d∅. Merk op dat dt de tijdsverandering is voor een hypothetische waarnemer ver weg van zwaartekrachtsinvloeden; het is geen direct gemeten tijd maar een theoretische coördinatentijd.
De daadwerkelijke tijd die door een klok op een bepaalde locatie wordt gemeten, is dτ, de eigen tijd.
We zullen de Schwarzschild-metriek gebruiken om een benaderde formule af te leiden die de tijdsdilatatie van de klokken beschrijft, op basis van hun positie en beweging. Daarna geven we ook de volledige (exacte) oplossing. Hoewel die laatste complexer is, is ze met behulp van computerprogramma’s zoals Excel goed hanteerbaar en levert ze een nauwkeurig resultaat.
4.1.1 Benaderde Formule voor Tijdsdilatatie
We benaderen de situatie waarin de klokken zich op cirkelvormige banen rond de aarde bevinden: óf op zeeniveau, óf op een bepaalde hoogte boven het aardoppervlak. Omdat de banen cirkelvormig zijn, geldt dat dr = 0. Bovendien nemen we aan dat de beweging plaatsvindt in het vlak van de evenaar, waardoor θ = π/2 constant is en dus dθ = 0.
Daarmee vereenvoudigt de Schwarzschild-metriek zich tot:
\[ c^2 d\tau^2=\left(1 - \frac{2GM}{c^2 r}\right) c^2 dt^2-r^2 d\phi^2 \tag{2} \]Delen door \(c^2\) geeft:
\[ d\tau^2=\left(1 - \frac{2GM}{c^2 r}\right) dt^2-\frac{r^2}{c^2} \left(\frac{d\phi}{dt} \right)^2 dt^2 \tag{3} \]Gebruikmakend van de definitie van de baansnelheid \(v=r \frac{d\phi}{dt}\), volgt:
\[ d\tau=\sqrt{1 - \frac{2GM}{c^2 r} - \frac{v^2}{c^2}}\, dt \tag{4} \]Omdat de termen \(\frac{2GM}{c^2r}\) en \(\frac{v^2}{c^2}\) zeer klein zijn ten opzichte van 1, passen we een eerste-orde Taylor-benadering toe:
\[ d\tau\approx\left(1-\frac{GM}{c^2 r}-\frac{v^2}{2c^2}\right)dt \tag{5} \]Aangezien \(r\) en \(v\) constant zijn, kunnen we direct integreren:
\[ \tau=\left(1-\frac{GM}{c^2 r}-\frac{v^2}{2c^2}\right) t+\tau_0 \tag{6} \]We vergelijken nu twee klokken. Klok 1 bevindt zich op het aardoppervlak, met straal \(r_1\), de afstand van het middelpunt van de aarde, en snelheid \(v_1\), als gevolg van de aardrotatie. Voor deze klok geldt:
\[ d\tau_1=\left(1-\frac{GM}{c^2 r_1}-\frac{v_1^2}{2c^2}\right)dt \tag{7} \]Voor klok 2, bijvoorbeeld in een vliegtuig op hoogte \(h\), met straal \(r_2\) en snelheid \(v_2\), geldt:
\[ d\tau_2=\left(1-\frac{GM}{c^2 r_2}-\frac{v_2^2}{2c^2}\right)dt \tag{8} \]De verhouding tussen beide tijdseenheden wordt dan:
\[ d\tau_2=\frac{1 - \frac{GM}{c^2 r_2} - \frac{v_2^2}{2c^2}}{1 - \frac{GM}{c^2 r_1} - \frac{v_1^2}{2c^2}}\, d\tau_1 \]Door gebruik te maken van de benadering: \[ (1-\varepsilon)^{-1} \approx 1+\varepsilon, \] volgt:
\[ d\tau_2 \approx \left( 1 - \frac{GM}{c^2 r_2} - \frac{v_2^2}{2c^2} \right) \left( 1 + \frac{GM}{c^2 r_1} + \frac{v_1^2}{2c^2} \right) d\tau_1 \]
\[ d\tau_2 \approx \left[ 1 + \frac{GM}{c^2 r_1} + \frac{v_1^2}{2c^2} - \frac{GM}{c^2 r_2}\left( 1 + \frac{GM}{c^2 r_1} + \frac{v_1^2}{2c^2} \right) - \frac{v_2^2}{2c^2}\left( 1 + \frac{GM}{c^2 r_1} + \frac{v_1^2}{2c^2} \right) \right] d\tau_1 \]
Daar de termen \(\frac{GM}{c^2 r_1}, \frac{v_1^2}{2c^2}, \frac{GM}{c^2 r_2}, \frac{v_2^2}{2c^2}\) zeer klein zijn, kunnen hun producten verwaarloosd worden. Hieruit volgt:
\[ d\tau_2 \approx \left[ 1 + \frac{GM}{c^2}\left(\frac{1}{r_1}-\frac{1}{r_2}\right) + \frac{v_1^2 - v_2^2}{2c^2} \right] d\tau_1 \tag{9} \]
Als we aannemen dat beide klokken starten bij \(\tau_1=\tau_2=0\), dan is de integratie direct:
\[ \tau_2 \approx \left[ 1 + \frac{GM}{c^2}\left(\frac{1}{r_1}-\frac{1}{r_2}\right) + \frac{v_1^2 - v_2^2}{2c^2} \right] \tau_1 \tag{10} \]
Vergelijking tussen klokken
Voor een klok op het aardoppervlak \((r_1, v_1)\) en een klok in een vliegtuig \((r_2, v_2)\):
\[ \tau_2 - \tau_1 \approx \left[ \frac{GM}{c^2}\left(\frac{1}{r_1}-\frac{1}{r_2}\right) + \frac{v_1^2 - v_2^2}{2c^2} \right]\tau_1 \tag{11} \]
Stel dat klok 1 zich op het aardoppervlak bevindt met straal \(R\), en klok 2 in een vliegtuig op hoogte \(h\). Dan is \(r_2 = R + h\). Omdat \(h \ll R\), kunnen we benaderen:
\[ \frac{1}{R} - \frac{1}{R+h} \approx \frac{h}{R^2} \quad\Rightarrow\quad \frac{GM}{c^2}\left(\frac{1}{R}-\frac{1}{R+h}\right) \approx \frac{gh}{c^2} \]
Dus:
\[ \tau_2 - \tau_1 \approx \left[ \frac{GM}{c^2}\left(\frac{1}{R}-\frac{1}{R+h}\right] + \frac{v_1^2 - v_2^2}{2c^2} \right)\tau_1 \tag{12} \]
Als we aannemen dat \(h/R \ll 1\) en \(g = GM/R^2\), dan:
\[ \tau_2 - \tau_1 = \left( \frac{gh}{c^2} - \frac{v_2^2 - v_1^2}{2c^2} \right)\tau_1 \tag{13} \]
Aangezien \(v_1 = v_{\text{earth}}\) (rotatiesnelheid aarde) en \(v_2 = v_{\text{plane}} + v_{\text{earth}}\), krijgen we:
\[ v_1^2 - v_2^2 = v_{\text{earth}}^2 - (v_{\text{plane}} + v_{\text{earth}})^2 = -v_{\text{plane}}^2 - 2 v_{\text{earth}} v_{\text{plane}} \]
Invullen in (13) geeft:
\[ \tau_{\text{plane}} - \tau_{\text{earth}} = \left( \frac{gh}{c^2} - \frac{v_{\text{plane}}(v_{\text{plane}} + 2v_{\text{earth}})}{2c^2} \right)\tau_{\text{earth}} \tag{14} \]
Deze vergelijking is volledig afgeleid uit de Schwarzschild‑vergelijking met enkele benaderingen. Ze stemt overeen met de benadering in het originele Hafele–Keating‑experiment.
Opmerking 1. Indien de snelheid van het vliegtuig als grondsnelheid wordt opgevat, kan op hoogte \(h\) benaderd worden:
\[ v_2=\frac{R + h}{R}\left(v_{\text{plane}} + v_{\text{earth}}\right) \]In dat geval dient de bovenstaande formule dienovereenkomstig aangepast te worden.
Opmerking 2. Een nauwkeurigere behandeling van \(v_1\) en \(v_2\) volgt in het volgende hoofdstuk, waar de snelheden specifieker worden afgeleid op basis van het gebruikte coördinatenstelsel.
4.1.2 Uitwerking van v1 en v2 in Vergelijking (13)
De snelheid \(v_1\) in vergelijking (3.1.1.13) is de snelheid van een stilstaand punt op de evenaar van het aardoppervlak. Deze wordt uitgedrukt als:
\[ v_1 = r_1 \frac{d\phi}{dt} \]waarbij dt de coördinatentijd is in het ‘universele’ referentiekader. Omdat metingen op het aardoppervlak echter plaatsvinden met betrekking tot de lokale eigen tijd \(\tau\), is een conversie nodig.
Met behulp van de kettingregel geldt:
\[ v_{1,t}= r_1 \frac{d\phi}{dt}= r_1 \frac{d\phi}{d\tau} \frac{d\tau}{dt}= v_{1,\tau} \frac{d\tau}{dt}\tag{14a} \]We gebruiken nu de Schwarzschild-metriek (in het equatoriale vlak en met \(dr = 0\)) om \(\frac{d\tau}{dt}\) te bepalen:
\[ c^2 d\tau^2=\left(1 - \frac{2GM}{c^2 r_1}\right)c^2 dt^2- r_1^2 \left(\frac{d\phi}{d\tau} \right)^2 d\tau^2 \]Na herordening volgt:
\[ \left[1 + \frac{r_1^2}{c^2}\left(\frac{d\phi}{d\tau}\right)^2 \right] d\tau^2=\left(1 - \frac{2GM}{c^2 r_1}\right) dt^2 \]We definiëren:
\[ \sigma^2 = 1 - \frac{2GM}{c^2 r} \]Dan geldt:
\[ \left(1 + \frac{v_{1,\tau}^2}{c^2}\right) d\tau^2= \sigma_1^2 dt^2 \] \[ \left(\frac{d\tau}{dt}\right)^2=\frac{\sigma_1^2}{1 + \frac{v_{1,\tau}^2}{c^2}}\tag{14b} \]Substitutie in vergelijking (14a) geeft:
\[ v_{1,t}^2=v_{1,\tau}^2\left(\frac{d\tau}{dt}\right)^2=v_{1,\tau}^2\frac{\sigma_1^2}{1 + \frac{v_{1,\tau}^2}{c^2}} \]Deze uitdrukking laat zien dat \(\frac{d\tau}{dt}\), de conversie tussen coördinatentijd en eigen tijd, afhankelijk is van de rotatiesnelheid van de aarde, \(v_{1,\tau}\), gemeten in lokale eigen tijd.
Beschouwen we nu een vliegtuig dat oostwaarts vliegt. De totale snelheid op aardniveau (gemeten in eigen tijd) is:
\[ v_{1\tau \text{_plane}}=v_{\text{plane_}\tau}+v_{1\tau \text{_earth}}=r_1 \frac{d\phi}{d\tau} \]waarbij:
- \(v_{\text{plane_}\tau}\): snelheid van het vliegtuig t.o.v. het aardoppervlak
- \(v_{1\tau \text{_earth}}\): rotatiesnelheid van de aarde
Hoeksnelheid in het universele frame
De bijbehorende hoeksnelheid in het universele frame is dan:
\[ r_1 \frac{d\phi}{dt} = r_1 \frac{d\phi}{d\tau}\frac{d\tau}{dt} = \left( v_{\text{plane_}\tau}+v_{1\tau \text{_earth}} \right) \frac{d\tau}{dt} \]
\[ \frac{d\tau}{dt} = \frac{\sigma_1}{\sqrt{\left(1 + \frac{v_{1\tau\text{_earth}}^{2}}{c^{2}}\right)}} \]
\[ \frac{d\phi}{dt} =\left( v_{\text{plane_}\tau}+v_{1\tau \text{_earth}} \right) \frac{\sigma_1}{r_1\sqrt{\left(1 + \frac{v_{1\tau\text{_earth}}^{2}}{c^{2}}\right)}} \]
Hier hebben we de rotatiesnelheid (hoeksnelheid) berekend in het universele frame. Dit is geldig voor elk niveau, ofwel elke afstand vanaf het middelpunt. Maar de snelheid zelf wordt bepaald door r maal deze hoeksnelheid.
Snelheid op niveau van het vliegtuig
\( v_{\text{plane},\tau} \) is de gemeten snelheid van het vliegtuig op grondniveau en ten opzichte van de eigen tijd, wat de enige beschikbare tijd is op dat niveau. \( v_{\text{earth},\tau} \) is de roterende snelheid van een stilstaand punt op aarde ten opzichte van het universele frame, maar gemeten met de eigen tijd op aardniveau.
De snelheid van het vliegtuig in het universele frame op hoogte \( r_2 \) is:
\[ v_{2t}=r_2 \frac{d\phi}{dt}=\frac{r_2}{r_1}\frac{\sigma_1}{\sqrt{1 + \frac{v_{1\tau \text{_earth}}^2}{c^2}}}\left( v_{\text{plane_}\tau}+v_{1\tau \text{_earth}} \right) \]We splitsen deze snelheid in een 'aardrotatie'- en een 'vliegtuig'-component:
\[ v_{2t} = v_{2t\text{_earth}} + v_{2t\text{_plane}} \]
Met:
\[ v_{2t\text{_earth}} = \frac{r_2}{r_1}\, \frac{\sigma_1 v_{1\tau\text{_earth}}}{\sqrt{1 + \frac{v_{1\tau\text{_earth}}^2}{c^2}}} \]
En:
\[ v_{2t\text{_plane}} = v_{2t} - v_{2t\text{_earth}} = \frac{r_2}{r_1}\, \frac{\sigma_1 v_{\text{plane_}\tau}}{\sqrt{1 + \frac{v_{1\tau\text{_earth}}^2}{c^2}}} \]
Samenvatting van het resultaat:
De conversie van snelheid op aardniveau naar het universele frame:
\[ v_{1t\text{_earth}} = v_{1\tau\text{_earth}} \, \frac{\sigma_{\text{earth}}}{1 + \sqrt{\frac{v_{1\tau\text{_earth}})^2}{c^2}}} \tag{15} \]
De snelheid \( v_2 \) van het vliegtuig in het universele frame is:
\[ v_{2t} = \frac{r_2}{r_1}\, \frac{ \sigma_{\text{earth}}\left(v_{\text{plane_}\tau} + v_{\text{earth_}\tau}\right) }{ \sqrt{1 + \frac{v_{1\tau\text{_earth}}^2}{c^2}} } \tag{16} \]
Substitutie in vergelijking (3.1.1._13):
\[ \tau_2 - \tau_1 = \left( \frac{gh}{c^2} - \frac{v_2^2 - v_1^2}{2c^2} \right) \tau_1 \tag{13} \]
wordt dan:
\[ \tau_2 - \tau_1 = \left( \frac{gh}{c^2} - \frac{ \sigma_{\text{earth}}^2 }{ 1 + \frac{(v_{1\tau\text{_earth}})^2}{c^2} } \cdot \frac{1}{2c^2} \left[ \left( \frac{R+h}{R} \right)^2 \left( v_{\tau\text{_plane}} + v_{\tau\text{_earth}} \right)^2 - v_{1\tau\text{_earth}}^2\right]\right) \;\tau_1 \tag{17} \]
Deze vergelijking beschrijft de tijdsdilatatie tussen een klok op het aardoppervlak en een klok aan boord van een vliegtuig, rekening houdend met zowel gravitationele als snelheidsafhankelijke effecten, alle gebaseerd op lokaal meetbare grootheden.
4.1.3 De Exacte Afleiding
In plaats van een benadering, maken we nu een exacte afleiding, volledig gebaseerd op de Schwarzschild-metriek. We beginnen bij vergelijking (4):
Aangezien \( r \) en \( v \) constant zijn, is de integratie eenvoudig:
Het doel is de eigen tijd van verschillende klokken met elkaar te vergelijken. Als referentie nemen we de klok op het aardoppervlak. Andere klokken bevinden zich in vliegtuigen, op grotere hoogte en met verschillende snelheden. Zelfs de klok op aarde heeft een niet-nul snelheid door de aardrotatie.
Voor de klok op het aardoppervlak (straal \( r_1 \), snelheid \( v_1 \)) geldt:
Voor de klok in het vliegtuig (straal \( r_2 \), snelheid \( v_2 \)):
Om de verhouding tussen de twee eigen tijden te vinden, delen we deze uitdrukkingen:
Bij gelijke begintijd \( \tau_2(0) = \tau_1(0) = 0 \), is de oplossing:
Tijdverschil tussen twee klokken
Stel \( r_1 = R \), de straal van de aarde, en \( r_2 = R + h \), de hoogte van het vliegtuig, dan wordt dit:
Snelheden en gravitationele effecten
In deze uitdrukking:
- \( v_1 \) is de rotatiesnelheid van een punt op het aardoppervlak (richting oost),
- \( v_2 \) is de snelheid van het vliegtuig ten opzichte van het universele referentiekader.
Beide snelheden werden eerder afgeleid in vergelijking 14b en 15b van hoofdstuk 4.1.5.
Door gebruik te maken van de Schwarzschildstraal \( R_s = \frac{2GM}{c^2} \), herschrijven we dit als:
Conclusie
Deze vergelijking is een exacte uitdrukking, rechtstreeks afgeleid uit de Schwarzschild-metriek. Ze toont hoe het verschil in eigen tijd tussen een klok op aarde en een klok in een vliegtuig beïnvloed wordt door:
- Gravitationele tijdsdilatatie: klokken op grotere hoogte (zwakkere zwaartekracht) lopen sneller.
- Kinematische tijdsdilatatie: klokken die sneller bewegen lopen trager.
Berekeningen gebaseerd op de uitgevoerde experimenten:
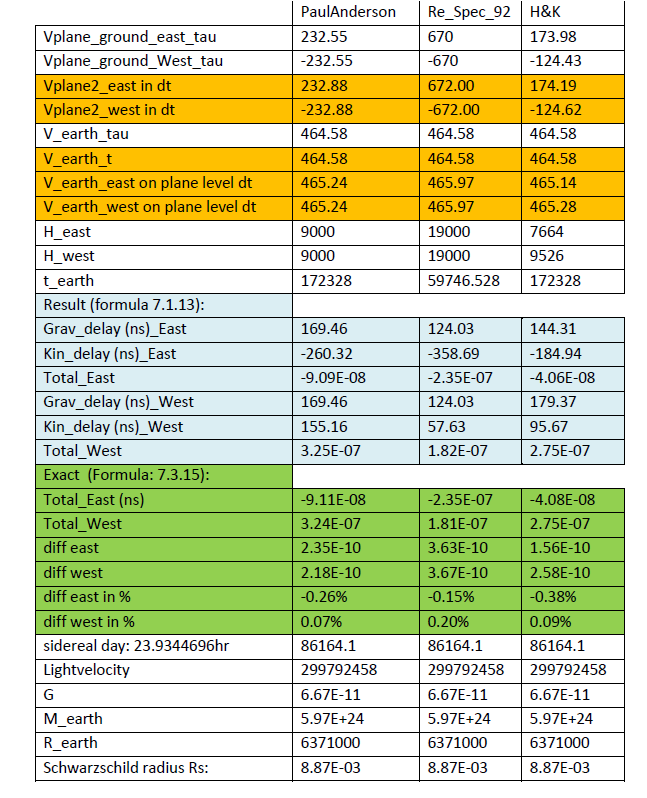
Conclusie
De benaderingen zijn correct binnen een nauwkeurigheid van 0.4%.
Praktische Toepassing
- Rotatiesnelheid aarde (evenaar): \( v_{\text{earth}} \) is ongeveer 464.58 m/s (op basis van de sterrendag).
- Vliegtuig: Snelheid t.o.v. aardoppervlak, gecorrigeerd voor hoogte.
- Hoogte-effect: \( h \) is typisch enkele kilometers, \( R \) (aarde) ongeveer \( 6.371 \times 10^{6}\,\text{m} \).
Resultaten en Interpretatie
- Oostwaarts vliegende klok: Grotere snelheid t.o.v. het aardcentrum → sterkere kinematische tijdsdilatatie → klok loopt achter.
- Westwaarts vliegende klok: Lagere snelheid t.o.v. het aardcentrum → zwakkere tijdsdilatatie → klok loopt voor.
- Gravitationeel effect: Klokken op grotere hoogte (vliegtuigen) lopen sneller door zwakkere zwaartekracht.
Experimentele Uitkomst
- De gemeten tijdsverschillen kwamen exact overeen met de voorspellingen van de algemene relativiteitstheorie, met een nauwkeurigheid van minder dan 0.4%.
- Zowel de benaderde als de exacte formules (afgeleid uit de Schwarzschild-metriek) zijn in overeenstemming met de waarnemingen.
Samenvatting
- Het Hafele–Keating-experiment is een directe, kwantitatieve bevestiging van Einsteins relativiteitstheorie.
- De Schwarzschild-metriek biedt het wiskundige kader voor het verklaren van deze tijdsdilatatie-effecten.
- Beide effecten — beweging en zwaartekracht — zijn essentieel en worden simultaan gemeten en verklaard.
4.1.4 De snelheid van een stilstaand punt op de evenaar aan het aardoppervlak
Om de snelheid van een stilstaand punt op de evenaar te berekenen, moeten we eerst de rotatietijd van de aarde bepalen: de sterrendag (sidereal day).
Sterrendag versus etmaal
Een gewone dag of etmaal (24 uur) is de tijd tussen twee opeenvolgende hoogste standen van de zon aan de hemel. Deze tijd is gebaseerd op de zonnecyclus, niet op de werkelijke rotatie van de aarde.
Door de jaarlijkse baan van de aarde rond de zon, maakt de aarde in één jaar één extra rotatie ten opzichte van de vaste sterrenhemel. In één jaar (365,25 zonne-etmalen) draait de aarde daarom 366,25 keer om haar as ten opzichte van de sterren.
Daaruit volgt de duur van één sterrendag:
\[ T_{\text{sidereal}}=\frac{365{,}25}{366{,}25}\cdot24\cdot3600=86164{,}1\ \text{s} \]
Dit is omgerekend:
\[ \frac{86164{,}1}{3600}=23{,}93447\ \text{uur} \]
Ofwel: 23 uur, 56 minuten en 4 seconden.
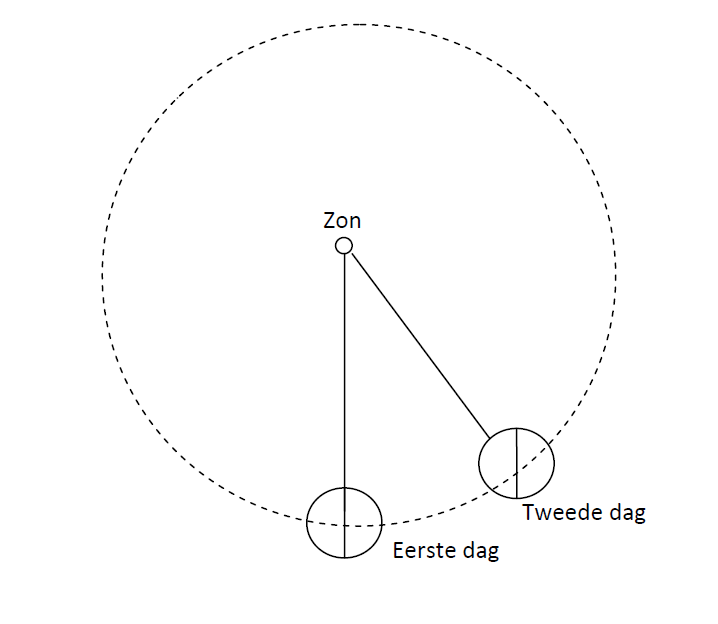
Snelheid op de evenaar
Met de straal van de aarde
\[ R = 6371 \ \text{km}=6{,}371 \times 10^{6} \ \text{m}, \]
kunnen we de omtrek aan de evenaar berekenen:
\[ \text{Omtrek}=2\pi R=2\pi \times 6{,}371 \times 10^{6}\approx4{,}003 \times 10^{7}\ \text{m}. \]
De snelheid van een stilstaand punt op de evenaar (ten opzichte van een niet-meedraaiend referentiekader) is dan:
\[ v_{\text{earth}}=\frac{2\pi R}{T_{\text{sidereal}}}=\frac{4{,}003 \times 10^{7}}{86164{,}1}=464{,}58\ \text{m/s}. \]
Ter vergelijking: als we ten onrechte een dag van 24 uur zouden nemen, krijgen we:
\[ v=\frac{2\pi R}{86400}=463{,}3\ \text{m/s}. \]
Samenvatting
- Een sterrendag duurt ongeveer 23 uur, 56 minuten en 4 seconden.
- De snelheid van een stilstaand punt op de evenaar is ongeveer 464,58 m/s.
- Het verschil tussen een sterrendag en een zonne-etmaal leidt tot een meetbaar verschil in snelheid, wat belangrijk is voor relativistische berekeningen, zoals in het Hafele–Keating-experiment.
4.1.5 Correctie op afleiding gebaseerd op Paul Anderson
In de oorspronkelijke afleiding van Anderson wordt de snelheid van het vliegtuig ingevoerd ten opzichte van het aardoppervlak. In zijn formule 3.1.1.3 is deze snelheid echter uitgedrukt ten opzichte van de coördinatietijd \(dt\), terwijl de klokken in beweging eigen tijd \(d\tau\) meten. Dit vereist een correctie: de snelheid van het object moet worden uitgedrukt ten opzichte van zijn eigen klok, dus via \(d\tau\).
Startpunt: De volledige Schwarzschild-relatie
We nemen als uitgangspunt vergelijking 2 uit hoofdstuk 4.1.1, zonder benadering:
\[ c^{2}\,d\tau^{2} = \left(1 - \frac{2GM}{c^{2}r}\right)c^{2}\,dt^{2} - r^{2}\,d\phi^{2} \tag{2} \]Delen door \(c^{2}\) geeft:
\[ d\tau^{2} = \left(1 - \frac{2GM}{c^{2}r}\right)dt^{2} - \frac{r^{2}}{c^{2}}\left(\frac{d\phi}{d\tau}\right)^{2}d\tau^{2} \tag{3b} \]We herschrijven dit als:
\[ d\tau^{2} \left(1 + \frac{r^{2}}{c^{2}}\left(\frac{d\phi}{d\tau}\right)^{2}\right)= \left(1 - \frac{2GM}{c^{2}r}\right)dt^{2} \tag{3c} \]En dus:
\[ d\tau = \sqrt{ \frac{1 - \dfrac{2GM}{c^{2}r}} {1 + \dfrac{r^{2}}{c^{2}}\left( \dfrac{d\phi}{d\tau}\right)^{2}} }\,dt \tag{4b} \]Met:
\[ v_{\tau} = r\,\frac{d\phi}{d\tau} \tag{4c} \]Dus:
\[ d\tau_{1} = \sqrt{ \frac{1 - \dfrac{2GM}{c^{2}r_{1}}}{1 + \dfrac{v_{1}^{2}}{c^{2}}}}\,dt \tag{7b} \] \[ d\tau_{2} =\sqrt{ \frac{1 - \dfrac{2GM}{c^{2}r_{2}}} {1 + \dfrac{v_{2}^{2}}{c^{2}}}}\,dt \tag{8b} \]We schrijven vervolgens:
\[ d\tau_{2}=\sqrt{\frac{1 - \dfrac{2GM}{c^{2}r_{2}}}{1 + \dfrac{v_{2}^{2}}{c^{2}}}}\sqrt{ \frac{1 + \dfrac{v_{1}^{2}}{c^{2}}}{1 - \dfrac{2GM}{c^{2}r_{1}}}}\,d\tau_{1} \tag{9b} \]Daaruit volgt de vergelijking tussen beide eigen tijden:
\[ \tau_{2}=\sqrt{\frac{1 - \dfrac{2GM}{c^{2}r_{2}}}{1 + \dfrac{v_{2}^{2}}{c^{2}}}}\sqrt{ \frac{1 + \dfrac{v_{1}^{2}}{c^{2}}}{1 - \dfrac{2GM}{c^{2}r_{1}}}}\,\tau_{1} \tag{10b} \]Als we \(\tau_{1} = \tau_{\text{earth}}\) nemen (klok op zeeniveau) en \(\tau_{2} = \tau_{\text{plane}}\), wordt:
\[ \tau_{\text{plane}} - \tau_{\text{earth}} =\left[\sqrt{\frac{1 - \dfrac{2GM}{c^{2}r_{2}}}{1 + \dfrac{v_{2}^{2}}{c^{2}}}}\sqrt{\frac{1 + \dfrac{v_{1}^{2}}{c^{2}}}{1 - \dfrac{2GM}{c^{2}r_{1}}}}- 1\right]\tau_{\text{earth}} \tag{11b} \]Hier is \(r_{1} = R\), de straal van de aarde. De afstand van de klok in een vliegtuig is dan \(R + h\). Dan krijgen we:
\[ \tau_{\text{plane}} - \tau_{\text{earth}}=\left[\sqrt{\frac{1 - \dfrac{2GM}{c^{2}(R + h)}} {1 + \dfrac{v_{\text{earth}}^{2}}{c^{2}}}}\sqrt{\frac{1 + \dfrac{v_{2}^{2}}{c^{2}}}{1 - \dfrac{2GM}{c^{2}R}}}- 1\right]\tau_{\text{earth}} \tag{14b} \]Of met Schwarzschild-radius \(R_{s} = \dfrac{2GM}{c^{2}}\):
\[ \tau_{\text{plane}} - \tau_{\text{earth}}=\left[\sqrt{\frac{1 - \dfrac{R_{s}}{R + h}} {1 + \dfrac{v_{\text{earth}}^{2}}{c^{2}}}}\sqrt{\frac{1 + \dfrac{v_{2}^{2}}{c^{2}}}{1 - \dfrac{R_{s}}{R}}}- 1\right]\tau_{\text{earth}} \tag{15b} \]Relatieve snelheid op vlieghoogte
De grondsnelheid van het vliegtuig (relatief t.o.v. het aardoppervlak) moet worden omgerekend naar een coördinatenonafhankelijke snelheid op vlieghoogte:
\[ v_{2}=\left(v_{\text{earth}} + v_{\text{plane (relative to earth point)}}\right)\cdot \frac{R + h}{R} \]Tot nu toe is de formule zonder benaderingen.
Na eerste-orde Taylorbenaderingen van vergelijking (14b), zoals eerder gedaan, wordt het resultaat:
\[ \tau_{\text{plane}} - \tau_{\text{earth}}=\left(\left[1 - \frac{GM}{c^{2}(R + h)}\right]\left[1 + \frac{GM}{c^{2}R}\right]\left[1 + \frac{v_{\text{earth}}^{2}}{2c^{2}}\right]\left[1 - \frac{v_{2}^{2}}{2c^{2}}\right]- 1\right)\tau_{\text{earth}} \tag{16} \]Dit kan worden herschreven als:
\[ \tau_{\text{plane}} - \tau_{\text{earth}}=\left(\left[1 + \frac{GM}{c^{2}}\left(\frac{1}{R} - \frac{1}{R + h}\right)\right]\left[1 + \frac{v_{\text{earth}}^{2} - v_{2}^{2}}{2c^{2}} \right]- 1\right)\tau_{\text{earth}} \tag{17} \] \[ \tau_{\text{plane}} - \tau_{\text{earth}}=\left(\left[1 + \frac{GM}{c^{2}}\frac{h}{R^{2}}\right] \left[1 + \frac{v_{\text{earth}}^{2} - v_{2}^{2}}{2c^{2}}\right]- 1\right)\tau_{\text{earth}} \tag{18} \] \[ \tau_{\text{plane}} - \tau_{\text{earth}}=\left(\frac{GM}{c^{2}}\frac{h}{R^{2}}+ \frac{v_{\text{earth}}^{2} - v_{2}^{2}}{2c^{2}}\right)\tau_{\text{earth}} \tag{19} \]Met \(g = \dfrac{GM}{R^{2}}\) volgt:
\[ \tau_{\text{plane}} - \tau_{\text{earth}}=\left(\frac{gh}{c^{2}}- \frac{v_{2}^{2} - v_{\text{earth}}^{2}}{2c^{2}}\right)\tau_{\text{earth}} \tag{20 } \]Opmerking over snelheden en referentiekaders
De snelheid van het vliegtuig wordt gegeven als de grondsnelheid. Het is niet direct duidelijk of deze gemeten is ten opzichte van de klok op aarde of de klok in het vliegtuig. Laten we aannemen dat de klok op aarde bedoeld is. In dat geval moeten we een conversie maken naar het niveau van het vliegtuig, wat betekent dat we de klok op dat niveau moeten beschouwen. Dit doen we via de tijd \(t\) in het universele frame.
Als we \(\dfrac{d\phi_{\text{earth}}}{dt}\) beschouwen, is dit de rotatiesnelheid van de aarde in het universele frame. We kunnen de snelheid van de aarde op zeeniveau vinden door \(\dfrac{d\phi_{\text{earth}}}{dt}\) te vermenigvuldigen met \(R\), de afstand vanaf het middelpunt. De snelheid van de aarde gezien vanaf het niveau van het vliegtuig is \((R + h) \dfrac{d\phi_{\text{earth}}}{dt}\). Voor het vliegtuig geldt hetzelfde: op zeeniveau is de relatieve vliegtuigsnelheid \(R\dfrac{d\phi_{\text{plane}}}{dt}\) en op vliegtuigniveau \((R + h)\dfrac{d\phi_{\text{plane}}}{dt}\).
Nu moeten \(\dfrac{d\phi_{\text{earth}}}{dt}\) en \(\dfrac{d\phi_{\text{plane}}}{dt}\) worden gevonden. We gebruiken uit hoofdstuk 4.1.5 vergelijking (4c):
\[ v_{\tau} = r\,\frac{d\phi}{d\tau}= r\,\frac{d\phi}{dt}\,\frac{dt}{d\tau}\;\Rightarrow\; \frac{d\phi}{dt}= \frac{v_{\tau}}{r}\,\frac{d\tau}{dt} \]Vervolgens gebruiken we uit hoofdstuk 4.1.5 vergelijking (3.1.5.4b):
\[ \frac{d\tau}{dt}=\sqrt{\frac{1 - \dfrac{2GM}{c^{2}r}}{1 + \dfrac{v_{\tau}^{2}}{c^{2}}}} \]Dus:
\[ \frac{d\phi}{dt} =\frac{v_{\tau}}{r}\frac{d\tau}{dt}=\frac{v_{\tau}}{r}\sqrt{\frac{1 - \dfrac{2GM}{c^{2}r}}{1 + \dfrac{v_{\tau}^{2}}{c^{2}}}} \]Alle componenten aan de rechterkant zijn bekend.
Op zeeniveau:
\[ \frac{d\phi_{\text{earth}}}{dt}=\frac{v_{\text{earth}}}{R}\sqrt{\frac{1 - \dfrac{2GM}{c^{2}R}}{1 + \dfrac{v_{\text{earth}}^{2}}{c^{2}}}} \]En voor het vliegtuig geldt analoog:
\[ \frac{d\phi_{\text{plane}}}{dt}=\frac{v_{\text{plane}}}{R}\sqrt{\frac{1 - \dfrac{2GM}{c^{2}R}} {1 + \dfrac{v_{\text{earth}}^{2}}{c^{2}}}} \]Nu op vliegtuigniveau:
\[ v_{2}=v_{2\tau\text{_earth}} + v_{2\tau\text{_plane}}=(R + h)\left(\frac{d\phi_{ \text{earth}}}{dt}+ \frac{d\phi_{\text{plane}}}{dt}\right) \]Daarmee:
\[ v_{2} = \frac{R+h}{R} \sqrt{ \frac{1 - \dfrac{2GM}{c^{2}R}} {1 + \dfrac{v_{\text{earth}}^{2}}{c^{2}}} } \left( v_{\text{earth}} + v_{\text{plane}} \right) \]Tot nu toe was \(v_{2}\) nog exact. Met een eerste-orde Taylorbenadering wordt:
\[ v_{2}=\frac{R + h}{R}\sqrt{\left( 1 - \frac{GM}{c^{2}R}\right)\left(1 - \frac{v_{\text{earth}}^{2}}{2c^{2}} \right)}\left(v_{\text{earth}} + v_{\text{plane}}\right) \]Dus, de relevante formule is:
\[ v_{2}\approx\frac{R + h}{R}\left(1 - \frac{GM}{c^{2}R}- \frac{v_{\text{earth}}^{2}}{2c^{2}}\right) \left( v_{\text{earth}} + v_{\text{plane}}\right) \]Resultaat na Taylorbenadering
Toegepast op vergelijking (14b), leidt dit na linearisatie tot:
\[ \tau_{\text{plane}} - \tau_{\text{earth}}=\left(\frac{gh}{c^{2}}- \frac{v_{2}^{2} - v_{\text{earth}}^{2}}{2c^{2}}\right)\tau_{\text{earth}} \]Conclusie
Deze herziene aanpak corrigeert de inconsistentie in de oorspronkelijke afleiding: snelheden dienen gerelateerd te zijn aan eigen tijd, niet aan coördinatietijd. Na correctie en Taylorbenadering blijkt dat de numerieke afwijking ten opzichte van de benadering in het vorige hoofdstuk minder dan \(0{,}4\%\) bedraagt – binnen de gewenste nauwkeurigheid.
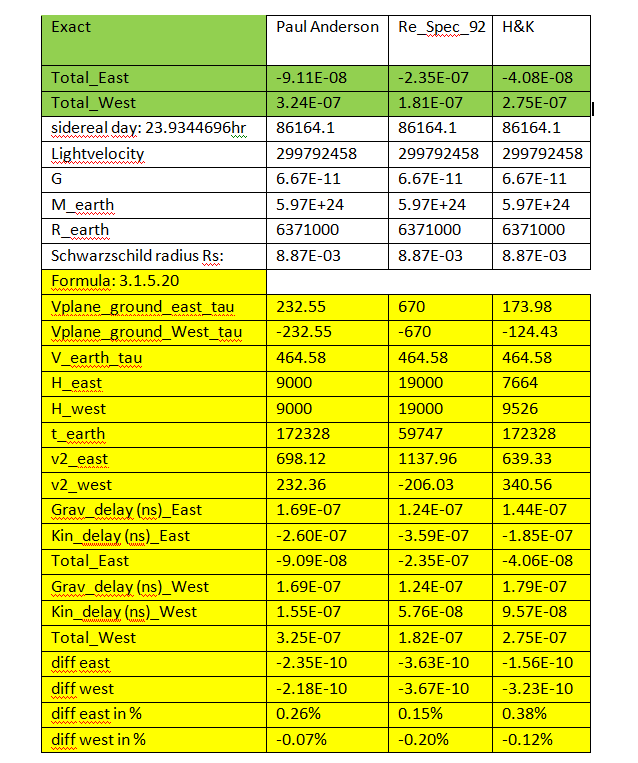
4.1.6 Overwegingen bij het Hafele-Keating-experiment en de Schwarzschild-metriek
We beginnen met de algemene Schwarzschild-vergelijking:
\[ ds^2 = c^2 d\tau^2 = \left(1 - \frac{2GM}{c^2 r}\right)c^2 dt^2 - \left(1 - \frac{2GM}{c^2 r}\right)^{-1} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta\, d\phi^2 \tag{1} \]
Zoals eerder gehanteerd, definiëren we:
\[ \sigma =\sqrt{ 1 - \frac{2GM}{c^2 r}} \]
Met deze notatie wordt vergelijking (1) herschreven als:
\[ ds^2 = c^2 d\tau^2 = \sigma^2 c^2 dt^2 - \sigma^{-2} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta\, d\phi^2 \tag{1a} \]
In het Hafele–Keating-experiment worden de tijd van de klok van het United States Naval Observatory (USNO) en de snelheid van een vliegtuig gemeten. De vraag luidt: wat vertegenwoordigen de tijd en de snelheid in de context van de Schwarzschild-metriek?
Er is een stationaire klok op zeeniveau op de evenaar, en twee vliegtuigen die zich bewegen in het equatoriale vlak — één naar het oosten, de ander naar het westen. Beide vliegtuigen volgen een cirkelvormige baan met constante snelheid ten opzichte van het aardoppervlak, maar in tegengestelde richtingen.
Aangezien het experiment plaatsvindt in het equatoriale vlak, nemen we aan dat \(\theta = \pi/2\) constant is, en dat \(r\) eveneens constant is wegens de cirkelvormige baan. De Schwarzschild-metriek vereenvoudigt zich dan tot:
\[ c^2 d\tau^2 = \left(1 - \frac{2GM}{c^2 r}\right)c^2 dt^2 - r^2 d\phi^2 \tag{2} \]
De coördinaten \(t, r, \theta, \phi\) in de Schwarzschild-metriek kunnen worden geïnterpreteerd als behorend tot een universeel (inertiaal) referentiestelsel waarin de aarde roteert. De klokken op het aardoppervlak en in de vliegtuigen bevinden zich elk in hun eigen lokaal inertiaal stelsel; hun gemeten tijd wordt weergegeven als de eigen tijd \(\tau\).
De universele coördinatietijd \(t\) is niet direct meetbaar, maar vormt een theoretische grootheid. Uit vergelijking (2) volgt:
\[ dt^2 = \frac{d\tau^2 + \frac{r^2}{c^2} d\phi^2}{1 - \frac{2GM}{c^2 r}} = \sigma^{-2}\left(d\tau^2 + \frac{r^2}{c^2} d\phi^2\right) = \sigma^{-2}\left(1 + \frac{r^2}{c^2}\left(\frac{d\phi}{d\tau}\right)^2\right)d\tau^2 \tag{4} \]
Onder de aanname \(t = 0\) wanneer \(\tau = 0\), leidt dit tot:
\[ t =\sigma^{-1}\sqrt{1 + \frac{r^2}{c^2}\left(\frac{d\phi}{d\tau}\right)^2}\,\tau= \sigma^{-1}\sqrt{1 + \frac{v^2}{c^2}}\,\tau \tag{4a} \]
waarbij \(v = r\, d\phi/d\tau\) de snelheid is ten opzichte van het universele frame.
Voor snelheden veel kleiner dan \(c\), kunnen we een eerste-orde Taylorbenadering toepassen:
\[ t = \sigma^{-1}\sqrt{1 + \frac{v^2}{c^2}}\,\tau = \frac{1}{\sigma\sqrt{1 - \frac{v^2}{c^2}}}\,\tau = \frac{\gamma}{\sigma}\, \tau \tag{4b} \]
met \[ \gamma =\frac{1}{ \sqrt{1 - \frac{v^2}{c^2}}} \] de Lorentzfactor.
Deze vergelijking drukt uit hoe de eigen tijd \(\tau\) van een bewegende klok relateert aan de coördinatietijd \(t\) in het Schwarzschild-stelsel.
4.2 Experiment 2 – Beweging van Deeltjes in Schwarzschild-Geometrie
De afleidingen in dit hoofdstuk zijn gebaseerd op:
- (Biesel, 2008) The Precession of Mercury’s Perihelion, Owen Biesel
- (Magnan) Christian Magnan: Complete calculations of the perihelion precession of Mercury and the deflection of light by the Sun in General Relativity
- (Pe’er, 2014) Asaf Pe’er: Schwarzschild Solution and Black Holes
We leiden vergelijkingen af voor de beweging van deeltjes in de Schwarzschild‑geometrie, als basis voor:
- De precessie van het perihelium van Mercurius,
- De afbuiging van licht door de zon,
- Het Shapiro‑experiment,
- De berekening van een kogelbaan.
We gebruiken de Schwarzschild‑metriek als uitgangspunt. Door de symmetrie in zowel de tijdcoördinaat \( t \) als de hoekcoördinaat \( \phi \) (geen metriekcomponent hangt van deze coördinaten af) geldt Noether’s stelling: elke continue symmetrie correspondeert met een behoudswet. Dit levert behoud van energie en behoud van impulsmoment.
Schwarzschild‑metriek
De metriek luidt:
\[ ds^2 = \sigma^2 c^2 dt^2 - \frac{dr^2}{\sigma^2} -\frac{r^2}{R^2_p} dR^2_p\,\theta^2 - \frac{r^2}{R^2_p} \sin^2\theta\, dR^2_p\,\phi^2 \]
Om de juiste dimensies te verkrijgen (alle coördinaten in meters), zetten we Rp=1m, waardoor de coëfficiënten dimensieloos worden. Dit leidt tot de meer gebruikelijke vorm:
\[ ds^2 = \sigma^2 c^2 dt^2 - \frac{dr^2}{\sigma^2} - r^2 d\theta^2 - r^2 \sin^2\theta\, d\phi^2 \tag{1a} \]
met:
\[ \sigma =\sqrt{ 1 - \frac{2GM}{c^2 r}} =\sqrt{ 1 - \frac{R_s}{r}}, \qquad R_s = \frac{2GM}{c^2} \]
Coëfficiënten van de metriek
\[ g_{00} = \sigma^2,\quad g_{11} = -\frac{1}{\sigma^2},\quad g_{22} = -r^2,\quad g_{33} = -r^2 \sin^2\theta \]
Contravariante componenten:
\[ g^{00} = \frac{1}{\sigma^2},\quad g^{11} = -\sigma^2,\quad g^{22} = -\frac{1}{r^2},\quad g^{33} = -\frac{1}{r^2 \sin^2\theta} \]
Verder: \[ \frac{d\sigma}{dr} = \frac{R_s}{2 r^2 \sigma} \]
Afgeleiden van metriekcomponenten
Voor de Schwarzschild‑metriek met \(\sigma = 1 - \dfrac{R_s}{r}\) vinden we de volgende afgeleiden:
\[ \frac{\partial g_{00}}{\partial r} = \frac{R_s}{r^2}, \qquad \frac{\partial g_{11}}{\partial r} = \frac{R_s}{r^2 \sigma^4}, \qquad \frac{\partial g_{22}}{\partial r} = -2r, \]
\[ \frac{\partial g_{33}}{\partial r} = -2r \sin^2\theta, \qquad \frac{\partial g_{33}}{\partial \theta} = -2 r^2 \sin\theta \cos\theta. \]
Christoffel‑symbolen
De Christoffel‑symbolen zijn gedefinieerd als:
\[ \Gamma^\rho_{\mu\nu} = \frac{1}{2} g^{\rho\alpha} \left( \frac{\partial g_{\nu\alpha}}{\partial x^\mu} + \frac{\partial g_{\mu\alpha}}{\partial x^\nu} - \frac{\partial g_{\mu\nu}}{\partial x^\alpha} \right) \]
Enkele relevante niet‑nul symbolen zijn:
\[ \Gamma^{0}_{10} = \Gamma^{0}_{01} = \frac{1}{2} g^{00} \left(\frac{\partial g_{00}}{\partial r}\right) = \frac{R_s}{2 r^2 \sigma^2}, \]
\[ \Gamma^{1}_{00} = \frac{1}{2} g^{11} \left(-\frac{\partial g_{00}}{\partial r}\right) = \frac{R_s}{2 r^2}\sigma^2, \qquad \Gamma^{1}_{11} = \frac{1}{2} g^{11} \left(\frac{\partial g_{11}}{\partial r}\right) = -\frac{R_s}{2 r^2 \sigma^2}, \]
\[ \Gamma^{1}_{22} =\frac{1}{2} g^{11} \left(\frac{-\partial g_{22}}{\partial r}\right) = -r \sigma^2, \qquad \Gamma^{1}_{33} =\frac{1}{2} g^{11} \left(-\frac{\partial g_{33}}{\partial r}\right) = -r \sigma^2 \sin^2\theta, \]
\[ \Gamma^{2}_{12} = \Gamma^{2}_{21} =\frac{1}{2} g^{22} \left(\frac{\partial g_{22}}{\partial r}\right) = \frac{1}{r}, \qquad \Gamma^{2}_{33} =\frac{1}{2} g^{22} \left(-\frac{\partial g_{33}}{\partial r}\right) = -\sin\theta\cos\theta, \]
\[ \Gamma^{3}_{13} = \Gamma^{3}_{31} =\frac{1}{2} g^{33} \left(\frac{\partial g_{33}}{\partial r}\right) = \frac{1}{r}, \qquad \Gamma^{3}_{23} = \Gamma^{3}_{32} =\frac{1}{2} g^{33} \left(\frac{\partial g_{33}}{\partial r}\right) = \cot\theta. \]
Alle overigen Christoffel-symbolen zijn nul.
Geodetische vergelijkingen
We beschouwen een geodetische wereldlijn, die de natuurlijke bewegingsbaan van een deeltje beschrijft in afwezigheid van niet-gravitationele krachten. De algemene geodetische vergelijking luidt:
\[ \frac{d^2 x^\alpha}{d\lambda^2} + \Gamma^\alpha_{\mu\nu} \frac{dx^\mu}{d\lambda} \frac{dx^\nu}{d\lambda} = 0 \]
Geodetische vergelijkingen per coördinaat
We werken de vier coördinaten uit, waarbij \( \lambda \) de affiene parameter is (maar hier gelijkgesteld kan worden aan de eigen tijd \( \tau \)):
Voor \( t \):
\[ \frac{d^2 t}{d\lambda^2} + \Gamma^{t}_{\mu\nu} \frac{dx^\mu}{d\lambda} \frac{dx^\nu}{d\lambda} = \frac{d^2 t}{d\lambda^2} + 2\,\Gamma^{0}_{10} \frac{dt}{d\lambda} \frac{dr}{d\lambda} = \frac{d^2 t}{d\lambda^2} + 2\,\frac{R_s}{2 r^2 \sigma^2} \frac{dt}{d\lambda} \frac{dr}{d\lambda} = 0 \]
Voor \( r \):
\[ \frac{d^2 r}{d\lambda^2} + \Gamma^{1}_{00}\left(\frac{dt}{d\lambda}\right)^2 + \Gamma^{1}_{11}\left(\frac{dr}{d\lambda}\right)^2 + \Gamma^{1}_{22}\left(\frac{d\theta}{d\lambda}\right)^2 + \Gamma^{1}_{33}\left(\frac{d\phi}{d\lambda}\right)^2 \]
\[ =\frac{d^2 r}{d\lambda^2} + \sigma^2 \frac{R_s}{2 r^2} \left(\frac{dt}{d\lambda}\right)^2 - \frac{R_s}{2 r^2 \sigma^2} \left(\frac{dr}{d\lambda}\right)^2 - r\sigma^2 \left(\frac{d\theta}{d\lambda}\right)^2 - r\sigma^2 \sin^2\theta \left(\frac{d\phi}{d\lambda}\right)^2 = 0 \]
Voor \( \theta \):
\[ \frac{d^2\theta}{d\lambda^2} + 2\,\Gamma^{2}_{12} \frac{dr}{d\lambda} \frac{d\theta}{d\lambda} + \Gamma^{2}_{33} \left(\frac{d\phi}{d\lambda}\right)^2 \]
\[ =\frac{d^2\theta}{d\lambda^2} + \frac{1}{r} \frac{dr}{d\lambda} \frac{d\theta}{d\lambda} - \cos\theta\sin\theta \left(\frac{d\phi}{d\lambda}\right)^2 = 0 \]
Voor \( \phi \):
\[ \frac{d^2\phi}{d\lambda^2} + 2\,\Gamma^{3}_{13} \frac{dr}{d\lambda} \frac{d\phi}{d\lambda} + 2\,\Gamma^{3}_{23} \frac{d\theta}{d\lambda} \frac{d\phi}{d\lambda} \]
\[ =\frac{d^2\phi}{d\lambda^2} + \frac{1}{r} \frac{dr}{d\lambda} \frac{d\phi}{d\lambda} + 2\cos\theta\sin\theta \frac{d\theta}{d\lambda} \frac{d\phi}{d\lambda} = 0 \]
Samengevat leiden deze vier componentvergelijkingen tot:
\[ \frac{d^2 t}{d\lambda^2} + 2\frac{R_s}{2 r^2 \sigma^2} \frac{dt}{d\lambda} \frac{dr}{d\lambda} = 0 \tag{1} \]
\[ \frac{d^2 r}{d\lambda^2} + \sigma^2 \frac{R_s}{2 r^2} \left(\frac{dt}{d\lambda}\right)^2 - \frac{R_s}{2 r^2 \sigma^2} \left(\frac{dr}{d\lambda}\right)^2 - r\sigma^2 \left(\frac{d\theta}{d\lambda}\right)^2 - r\sigma^2 \sin^2\theta \left(\frac{d\phi}{d\lambda}\right)^2 = 0 \tag{2} \]
\[ \frac{d^2\theta}{d\lambda^2} + \frac{1}{r} \frac{dr}{d\lambda} \frac{d\theta}{d\lambda} - \cos\theta\sin\theta \left(\frac{d\phi}{d\lambda}\right)^2 = 0 \tag{3} \]
\[ \frac{d^2\phi}{d\lambda^2} + \frac{1}{r} \frac{dr}{d\lambda} \frac{d\phi}{d\lambda} + 2\cos\theta\sin\theta \frac{d\theta}{d\lambda} \frac{d\phi}{d\lambda} = 0 \tag{4} \]
Elegante aanpak volgens Asaf Pe’er
We zullen eerst de elegante aanpak van Asaf Pe’er volgen uit zijn artikel “Schwarzschild Solution and Black Holes” (Pe’er, 2014), om vervolgens een eenvoudiger benadering te presenteren.
Volgens Asaf Pe’er:
“Op het eerste gezicht lijkt er niet veel hoop te zijn om dit stel van vier gekoppelde vergelijkingen eenvoudig op te lossen. Gelukkig wordt onze taak sterk vereenvoudigd door de hoge mate van symmetrie van de Schwarzschild‑metriek.”
De Schwarzschild‑ruimte heeft vier Killing‑velden: drie vanwege de sferische symmetrie, en één vanwege tijdtranslatie. Elk Killing‑veld leidt via Noether’s stelling tot een constante van de beweging voor een vrij deeltje.
Als \( K_\mu \) een Killing‑veld is, geldt:
\[ K_\mu \frac{dx^\mu}{d\lambda} = \text{constant} \tag{5} \]
Daarnaast is er een andere constante van beweging die volgt uit metrische compatibiliteit. Langs een geodetische wereldlijn geldt:
\[ ds^2 = g_{\mu\nu} dx^\mu dx^\nu, \qquad \left(\frac{ds}{d\lambda}\right)^2 = c^2 \left(\frac{d\tau}{d\lambda}\right)^2 = c^2 \varepsilon = g_{\mu\nu} \frac{dx^\mu}{d\lambda} \frac{dx^\nu}{d\lambda} \tag{6} \]
Hierbij is:
- \( \varepsilon = 1 \) voor massieve deeltjes,
- \( \varepsilon = 0 \) voor fotonen (massaloos),
- \( \varepsilon = -1 \) voor ruimtelijke geodeten.
Gebruik van symmetrieën en behoudswetten
In plaats van direct de vier gekoppelde geodetische vergelijkingen op te lossen, maken we gebruik van de symmetrieën die via Killing‑velden leiden tot behoudswetten.
In vlakke ruimte‑tijd leiden de symmetrieën (via Noether) tot bekende behouden grootheden:
- Tijdtranslatie‑invariantie → energiebehoud,
- Rotatie‑invariantie → behoud van impulsmoment.
Voor de Schwarzschild‑metriek geldt analoog:
- Beweging in een vlak: Het impulsmoment behoudt zijn richting → het deeltje beweegt in een vlak. Door coördinatenrotatie mogen we dat kiezen als het evenaarsvlak: \[ \theta = \frac{\pi}{2} \tag{7} \]
- Behoud van energie: Het tijdachtige Killing‑veld is: \[ K^\mu = (1,0,0,0)_T \] De geassocieerde covariante component is: \[ K_\mu = g_{\mu\nu} K^\nu = \left(1 - \frac{2GM}{c^2 r},\, 0,\, 0,\, 0\right) \tag{8} \] Hieruit volgt: \[ K_\mu \frac{dx^\mu}{d\lambda} = \left(1 - \frac{2GM}{c^2 r}\right)\frac{dt}{d\lambda} = \frac{E}{c^2} \tag{9} \] of gedefinieerd als: \[ k = \left(1 - \frac{2GM}{c^2 r}\right)\frac{dt}{d\lambda} = \frac{E}{c^2} \tag{9a} \]
- Behoud van impulsmoment: De Killing‑vector voor rotaties in \( \phi \) is: \[ L^\mu = (0,0,0,-1)_T \] De covariante component is: \[ L_\mu = g_{\mu\nu} L^\nu = (0,0,0,-r^2 \sin^2\theta) \tag{10} \] Bij \( \theta = \pi/2 \) is \( \sin\theta = 1 \), zodat: \[ r^2 \frac{d\phi}{d\lambda} = L \tag{11} \]
Hieruit volgen de behouden grootheden:
- \( E \): energie per eenheid massa,
- \( L \): impulsmoment per eenheid massa.
Voor fotonen zijn dit respectievelijk de energie en het impulsmoment zelf. (meer over het impulsmoment, zie Appendix 10.)
Merk op dat vergelijking (11) het equivalent is van Keplers tweede wet binnen de algemene relativiteit: gelijke oppervlakken worden in gelijke tijden doorlopen.
Alternatieve afleiding
Hoewel Asaf Pe’er opmerkt dat het oplossen van de volledige set gekoppelde geodetische vergelijkingen complex lijkt, blijkt dat een aantal van deze vergelijkingen relatief eenvoudig oplosbaar zijn. We tonen dit aan met behulp van vergelijkingen (3.2.1) en (3.2.4).
Stap 1 — Gebruik van vergelijking (3.2.1)
\[ \frac{d^2 t}{d\lambda^2} + 2\,\frac{R_s}{2 r^2 \sigma^2} \frac{dt}{d\lambda} \frac{dr}{d\lambda} = 0 \tag{3.2.1} \]
waarbij: \[ \sigma^2 =1 - \frac{2GM}{c^2r}.= 1 - \frac{R_s}{r}. \]
We vermenigvuldigen beide zijden met \( \sigma^2 \):
\[ \sigma^2 \frac{d^2 t}{d\lambda^2} + \frac{R_s}{r^2} \frac{dt}{d\lambda} \frac{dr}{d\lambda} = 0. \]
Omdat \( \sigma^2 = 1 - \frac{R_s}{r} \), herschrijven we dit als:
\[ \left(1 - \frac{R_s}{r}\right)\frac{d^2 t}{d\lambda^2} + \frac{R_s}{r^2} \frac{dt}{d\lambda} \frac{dr}{d\lambda} = 0. \]
We herschrijven dit:
\[ \frac{d^2 t}{d\lambda^2} + \frac{R_s}{r^2} \frac{dt}{d\lambda} \frac{dr}{d\lambda} - \frac{R_s}{r} \frac{d^2 t}{d\lambda^2} = 0 \]
Of:
\[ \frac{d}{d\lambda} \left( \frac{dt}{d\lambda} - \frac{R_s}{r}\frac{dt}{d\lambda} \right) = 0 \]
Dus: \[ \frac{d}{d\lambda} \left[ \frac{dt}{d\lambda}\left(1 - \frac{R_s}{r}\right) \right] = 0 \]
Dit toont aan dat de uitdrukking \[ \frac{dt}{d\lambda}\left(1 - \frac{R_s}{r}\right) \] constant is langs de wereldlijn.
We herkennen hierin de behouden grootheid die gerelateerd is aan de totale energie per massa‑eenheid van het deeltje. Vermenigvuldiging met \( c \) geeft:
\[ \frac{cdt}{d\lambda}\left(1 - \frac{R_s}{r}\right) = \text{constant} = \frac{E}{c}\, \left(\text{total energy}\right) \tag{9} \]
Stap 2 — Gebruik van vergelijking (3.2.4)
We gaan nu verder met vergelijking (3.2.4). Om de afleiding te vereenvoudigen nemen we aan dat het deeltje zich beweegt in het equatoriale vlak, zodat: \[ \theta = \frac{\pi}{2}. \]
Dan wordt vergelijking (3.2.4):
\[ \frac{d^2 \Phi}{d\lambda^2} + \frac{2}{r} \frac{dr}{d\lambda} \frac{d\Phi}{d\lambda} + 2\frac{\cos\theta}{ \sin\theta}\, \frac{d\theta}{d\lambda} \frac{d\Phi}{d\lambda} = 0. \]
Omdat in het equatoriale vlak \[ \theta = \frac{\pi}{2} \quad\Rightarrow\quad \cos\theta = 0,\;\; \sin\theta = 1, \] verdwijnt de laatste term en blijft over:
\[ \frac{d^2 \Phi}{d\lambda^2} + \frac{2}{r} \frac{dr}{d\lambda} \frac{d\Phi}{d\lambda} = 0. \]
Dit leidt tot:
\[ \frac{1}{r^2}\frac{d}{d\lambda}\left(r^2 \frac{d\phi}{d\lambda}\right)=0 \]
Wat betekent dat ook:
\[ r^2\frac{d\phi}{d\lambda} \]een constante is langs de geodetische wereldlijn. Deze constante herkennen we als het impulsmoment per eenheid massa:
\[ r^2\frac{d\phi}{d\lambda}=constant=L\left(impulsmoment\right) \tag{11} \]Samenvatting van de behouden grootheden
Door de symmetrieën zijn er dus twee behouden grootheden:
-
Energie per eenheid massa:
\[ \left(1 - \frac{R_s}{r}\right)\frac{dt}{d\lambda} = \frac{E}{c^2} \] -
Impulsmoment per eenheid massa:
\[ L = r^2\,\frac{d\Phi}{d\lambda} \]
4.2.1 Het Gravitatiepotentiaal
Met de eerder afgeleide behoudswetten kunnen we nu de beweging van deeltjes in de Schwarzschild-metriek verder analyseren. We beginnen met het uitschrijven van vergelijking (6), waarbij we gebruikmaken van de behouden grootheden uit vergelijkingen (10) en (11):
\[ \left( 1 - \frac{2GM}{c^{2} r} \right) c^{2} \left( \frac{dt}{d\lambda} \right)^{2} - \left( 1 - \frac{2GM}{c^{2} r} \right)^{-1} \left( \frac{dr}{d\lambda} \right)^{2} - r^{2} \left( \frac{d\phi}{d\lambda} \right)^{2} = c^{2} \varepsilon \tag{12} \]Invullen van de behouden grootheden E en L geeft:
\[ \left( 1 - \frac{2GM}{c^{2} r} \right) c^{2} \left( \frac{dt}{d\lambda} \right)^{2} - \left( 1 - \frac{2GM}{c^{2} r} \right)^{-1} \left( \frac{dr}{d\lambda} \right)^{2} - \frac{L^{2}}{r^{2}} = c^{2} \varepsilon \]We vermenigvuldigen deze vergelijking met \( 1 - \frac{2GM}{c^{2} r} \) en gebruiken \( \frac{E}{c} = c \frac{dt}{d\lambda} \left( 1 - \frac{2GM}{c^{2} r} \right) \) en \( L = r^{2} \frac{d\phi}{d\lambda} \) om te herschrijven:
\[ \left( 1 - \frac{2GM}{c^{2} r} \right)^{2} c^{2} \left( \frac{dt}{d\lambda} \right)^{2} - \left( \frac{dr}{d\lambda} \right)^{2} - \left( 1 - \frac{2GM}{c^{2} r} \right) \frac{L^{2}}{r^{2}} + c^{2} \varepsilon = 0 \]Invullen van de uitdrukking voor E leidt tot:
\[ \frac{E^{2}}{c^{2}} - \left( \frac{dr}{d\lambda} \right)^{2} - \left( 1 - \frac{2GM}{c^{2} r} \right) \frac{L^{2}}{r^{2}} + c^{2} \varepsilon = 0 \tag{13} \]We zijn hiermee in staat geweest om de vier gekoppelde geodetische vergelijkingen te reduceren tot één differentiaalvergelijking voor \( r(\lambda) \). Dit betekent een grote vereenvoudiging van het probleem.
We herschrijven vergelijking (13) in de volgende vorm:
\[ \frac{1}{2} \left( \frac{dr}{d\lambda} \right)^{2} + V(r) = \frac{1}{2} \frac{E^{2}}{c^{2}} \tag{14} \]met de effectieve potentiaal \( V(r) \) gedefinieerd als:
\[ V(r) = \frac{1}{2} c^{2} \varepsilon - \frac{\varepsilon GM}{r} + \frac{L^{2}}{2 r^{2}} - \frac{GM L^{2}}{c^{2} r^{3}} \tag{15} \]Vergelijking (14) is formeel identiek aan de klassieke vergelijking voor de beweging van een deeltje (met eenheidsmassa) in een één-dimensionaal potentiaal \( V(r) \), waarbij de totale “energie” \( \frac{1}{2} \frac{E^{2}}{c^{2}} \) is. Natuurlijk is de werkelijke energie \( E \), maar deze vorm maakt de vergelijking analoog aan de klassieke mechanica.
Als we het potentiaal \( V(r) \) in vergelijking (15) analyseren, zien we dat het slechts op één punt verschilt van het Newtoniaanse potentiaal: de laatste term. Deze term, evenredig met \( 1/r^{3} \), vertegenwoordigt een puur relativistische correctie en speelt vooral bij kleine \( r \) een belangrijke rol.
De termen kunnen als volgt worden geïnterpreteerd:
- De eerste term is constant (rustenergie voor massieve deeltjes), afhankelijk van \( \varepsilon = 1 \) voor massieve deeltjes en \( \varepsilon = 0 \) voor fotonen;
- De tweede term is het Newtoniaanse gravitationele potentiaal;
- De derde term is het klassieke impulsmomentpotentiaal;
- De vierde term is de relativistische correctie.
Let op: ondanks de vormelijke overeenkomst met de klassieke mechanica beschrijft dit géén de beweging van een deeltje dat vrij in één dimensie beweegt. In werkelijkheid gaat het om een deeltje dat een baan beschrijft rond een massief object. De relevante grootheden zijn niet alleen \( r(\lambda) \), maar ook \( t(\lambda) \) en \( \phi(\lambda) \), die samen het volledige ruimtetijdtraject beschrijven.
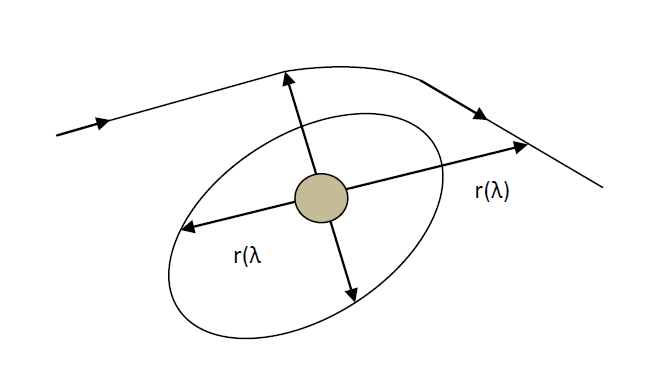
4.2.2 Intermezzo over Energie in Schwarzschild-geometrie
In dit intermezzo analyseren we de vorm van de energie zoals afgeleid in vergelijking (3.2.9) van hoofdstuk 4.2. Deze energie is een behouden grootheid in de Schwarzschild-geometrie.
We beginnen bij de relatie:
\[ \left( 1 - \frac{2GM}{c^{2} r} \right) \frac{dt}{d\lambda} = \frac{E}{m c^{2}} = \sigma^{2} \frac{dt}{d\lambda} \tag{9} \]Waaruit volgt:
\[ E = \sigma^{2} m c^{2} \frac{dt}{d\lambda} \]De Schwarzschild-metriek luidt:
\[ ds^{2} = c^{2} d\tau^{2} = \sigma^{2} c^{2} dt^{2} - \frac{dr^{2}}{\sigma^{2}} - r^{2} d\theta^{2} - r^{2} \sin^{2}\theta \, d\phi^{2} \]We gebruiken een affiene parameter \( \lambda \) met \( d\tau = d\lambda \) en beperken ons tot het equatoriale vlak \( \theta = \frac{\pi}{2} \).
\[ \sigma^{2} c^{2} \left( \frac{dt}{d\lambda} \right)^{2} - \sigma^{-2} \left( \frac{dr}{d\lambda} \right)^{2} - r^{2} \left( \frac{d\phi}{d\lambda} \right)^{2} = c^{2} \varepsilon \]Door te herschrijven naar snelheden ten opzichte van de coördinaattijd \( t \), verkrijgen we:
\[ \sigma^{2} c^{2} \left(\frac{dt}{d\lambda}\right)^{2} \;-\; \sigma^{-2} \left(\frac{dr}{dt}\right)^{2} \left(\frac{dt}{d\lambda}\right)^{2} \;-\; r^{2} \left(\frac{d\Phi}{dt}\right)^{2} \left(\frac{dt}{d\lambda}\right)^{2} = c^{2}\,\varepsilon \]
Voor massieve deeltjes geldt \( \varepsilon = 1 \):
\[ \sigma^{2} \left( \frac{dt}{d\lambda} \right)^{2} \left( 1 - \frac{\sigma^{-2} \left( \frac{dr}{dt} \right)^{2} + r^{2} \left( \frac{d\phi}{dt} \right)^{2}}{\sigma^{2} c^{2}} \right) =\varepsilon= 1 \tag{9a} \] \[ \left( \frac{dt}{d\lambda} \right)^{2}\left( 1 - \frac{v^2}{\sigma^2c^2}\right) =\frac{1}{\sigma^2} \]waaruit volgt:
\[ \frac{dt}{d\lambda} = \frac{1}{\sigma} \frac{1}{\sqrt{1 - \frac{v^{2}}{\sigma^{2} c^{2}}}} \]Waarbij \( v^{2} = \sigma^{-2} \left( \frac{dr}{dt} \right)^{2} + r^{2} \left( \frac{d\phi}{dt} \right)^{2} \) de totale snelheid is. In combinatie met de energie (vergelijking 9) leidt dit tot:
\[ E = \sigma^{2} m c^{2} \frac{dt}{d\lambda} = \frac{\sigma m c^{2}} {\sqrt{1 - \frac{v^{2}}{\sigma^{2} c^{2}}}} = \gamma_\sigma \sigma m c^{2} \]Deze behouden energie bestaat uit:
- Rustenergie: \( E_{0} = \sigma m c^{2} \)
- Relativistische kinetische energie: \[ E_{\text{kin}} = \sigma m c^{2} \left( \frac{1}{\sqrt{1 - \frac{v^{2}}{\sigma^{2} c^{2}}}} - 1 \right) \]
In het niet-relativistische limiet \( v \ll c \), en met een eerste-orde-Taylorontwikkeling van de wortel, vinden we de “kinetische” energie:
\[ E_{\text{kin}} \approx \sigma m c^{2} \left( 1+\frac{v^{2}}{2\sigma^{2}c^2}-1 \right)= \frac{m v^{2}}{2 \sigma} \]4.2.2.1 Alternatieve benadering via de metriek
Begin met de Schwarzschild-vergelijking:
\[ ds^2 = c^2 d\tau^2 = \sigma^2 c^2 dt^2 - \sigma^{-2} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta\, d\phi^2 \]
Voor het equatoriale vlak \(\theta = \pi/2\) en met een affiene parameter \(\lambda\) geldt:
\[ \sigma^2 c^2 \left(\frac{dt}{d\lambda}\right)^2 - \sigma^{-2} \left(\frac{dr}{d\lambda}\right)^2 - r^2 \left(\frac{d\phi}{d\lambda}\right)^2 = c^2 \varepsilon \]
Vermenigvuldig met \(\sigma^2\):
\[ \sigma^4 c^2 \left(\frac{dt}{d\lambda}\right)^2 - \left(\frac{dr}{d\lambda}\right)^2 - \sigma^2 r^2 \left(\frac{d\phi}{d\lambda}\right)^2 = \sigma^2 c^2 \varepsilon \]
Gebruik opnieuw:
\[ E = \sigma^2 m c^2 \frac{dt}{d\lambda} \quad \Rightarrow \quad \frac{E}{m c} = \sigma^2 c \frac{dt}{d\lambda} \]
Dan volgt:
\[ \left(\frac{E}{m c}\right)^2 = \left(\frac{dr}{d\lambda}\right)^2 + \sigma^2 r^2 \left(\frac{d\phi}{d\lambda}\right)^2 + \sigma^2 c^2 \varepsilon \]
Stel:
\[ r^2 \frac{d\phi}{d\lambda} = \frac{L}{m} \quad \Rightarrow \quad r^2 \left(\frac{d\phi}{d\lambda}\right)^2=\frac{L^2}{r^2m^2}=\frac{\left(mv_tr\right)^2}{r^2m^2} = v_t^2 \]
Neem nu \(\lambda = \tau\) en \(\varepsilon = 1\):
\[ \left(\frac{E}{m c}\right)^2 = \left(\frac{dr}{d\tau}\right)^2 + \sigma^2 v_t^2 + \sigma^2 c^2=v_r^2 + \sigma^2 v_t^2 + \sigma^2 c^2 \]
\[ \frac{E^2}{c^2} = m^2 v_r^2 + m^2 \sigma^2 v_t^2 + m^2 \sigma^2 c^2 \]
waarbij:
- \(v_r = \dfrac{dr}{d\tau}\) de radiale snelheid is,
- \(v_t = r \dfrac{d\phi}{d\tau}\) de transversale snelheid is.
De termen interpreteren we als:
- \(m v_r\): radiale impuls
- \(m \sigma v_t\): transversale impuls
- \(\sigma m c^2\): rustenergie
De kinetische energie wordt dan:
\[ E_{\text{kin}} = m c\sqrt{v_r^2 + \sigma^2 v_t^2} \]
4.2.2.2 Derde benadering: via een relativistische energie-impulsrelatie
Start opnieuw met de norm van de 4-snelheid:
\[ \sigma^2 c^2 \left(\frac{dt}{d\lambda}\right)^2 - \sigma^{-2} \left(\frac{dr}{d\lambda}\right)^2 - r^2 \left(\frac{d\phi}{d\lambda}\right)^2 = c^2 \varepsilon \]
Dit leidt tot:
\[ \left(\frac{E}{\sigma c}\right)^2 - \sigma^{-2} \left(\frac{dr}{d\lambda}\right)^2 - r^2 \left(\frac{d\phi}{d\lambda}\right)^2 = c^2 \varepsilon \]
\[ \frac{E^2}{\sigma^2 c^2} - p^2 = c^2 \varepsilon \quad \Rightarrow \quad E^2 = \sigma^2 c^4 \varepsilon + \sigma^2 c^2 p^2 \]
Waarbij \(p\) het totale ruimtelijke momentum per eenheid massa is. In rust volgt \(E=\sigma m c^2 \) en voor een foton \(E=\sigma p c \). In het algemeen geldt:
\[ E^2 = \sigma^2 m^2 c^4 \varepsilon + \sigma^2 m^2 c^2 U^2 \]
Waarbij:
\[ U^2 =\left(\frac{dx^\mu}{d\tau}\right)^2= \sigma^{-2} \left(\frac{dr}{d\tau}\right)^2 + r^2 \left(\frac{d\phi}{d\tau}\right)^2 \]
de kwadratische norm is van de ruimtelijke snelheid. Voor massieve deeltjes (\(\varepsilon=1\)) en eenheid massa wordt dit:
\[ E^2 = \sigma^2 c^4 + \sigma^2 c^2 U^2 \]
4.2.3 Samenvatting
- De Schwarzschild-metriek en de daaruit afgeleide geodetische vergelijkingen vormen het fundament voor vele relativistische experimenten.
- Symmetrieën en behouden grootheden reduceren de bewegingsvergelijkingen tot hanteerbare vormen.
- De effectieve potentiaal omvat zowel klassieke als relativistische effecten zoals lichtafbuiging, periheliumprecessie en Shapiro-vertraging.
4.3 Experiment 3 - Afbuiging van Licht
4.3.1 Historische en theoretische achtergrond
De afbuiging van licht door zwaartekracht was de eerste experimentele toets van de algemene relativiteitstheorie. In de klassieke Newtoniaanse zwaartekracht beweegt licht, als massaloos verschijnsel, in rechte lijnen die niet door zwaartekracht worden beïnvloed. Volgens de algemene relativiteitstheorie echter, volgt licht de kromming van de ruimte-tijd, veroorzaakt door massa.
Daardoor wijkt een lichtstraal af van een rechte lijn wanneer zij passeert langs een massief object zoals de zon. Dit effect kan waargenomen worden wanneer we kijken naar het licht van een ster die zich visueel dicht bij de zon bevindt.
Wanneer het licht van de ster langs de zon schampt, wordt het afgebogen, zodat de ster op een andere plaats aan de hemel lijkt te staan dan waar zij zich werkelijk bevindt. Een half jaar later, als de ster zich aan de andere kant van de hemel bevindt, zal haar licht de zon op grote afstand passeren, en wordt haar positie correct waargenomen.
Om dit effect zichtbaar te maken is een zonsverduistering nodig, omdat het zonlicht anders het sterlicht overstraalt. In 1919 werd dit effect voor het eerst gemeten door Arthur Eddington tijdens een totale zonsverduistering. Zijn waarnemingen bevestigden Einsteins voorspelling en betekenden een grote doorbraak in de acceptatie van de algemene relativiteitstheorie.
4.3.2 De afleiding van de afbuigingshoek
We beschouwen een lichtstraal (foton) die nadert vanuit het oneindige en langs de zon beweegt. De beweging van het foton in de Schwarzschild-ruimte wordt beschreven door de effectieve energievergelijking, zoals afgeleid in hoofdstuk 4.2.1.
Voor een foton geldt \(\varepsilon = 0\), zodat:
\[ \frac{1}{2}\left(\frac{dr}{d\lambda}\right)^2 + V(r) = \frac{1}{2}\frac{E^2}{c^2} \tag{14} \]
met:
\[ V(r) = \frac{1}{2}c^2\varepsilon - \varepsilon \frac{GM}{r} + \frac{L^2}{2r^2} - \frac{GM L^2}{c^2 r^3} \tag{15} \]
waarbij \(L\) het impulsmoment en \(E\) de energie van het foton zijn.
Voor \(\varepsilon = 0\) volgt:
\[ \frac{1}{2}\left(\frac{dr}{d\lambda}\right)^2 + \frac{L^2}{2r^2} - \frac{GM L^2}{c^2 r^3} = \frac{1}{2}\frac{E^2}{c^2} \]
We delen door \(L^2\) en vermenigvuldigen met 2:
\[ \frac{1}{L^2}\left(\frac{dr}{d\lambda}\right)^2 + \frac{1}{r^2} - \frac{2GM}{c^2 r^3} = \frac{E^2}{c^2 L^2} \]
Of equivalent:
\[ \frac{1}{L^2}\left(\frac{dr}{d\lambda}\right)^2 + \frac{1}{r^2} \left(1 - \frac{2GM}{c^2 r}\right) = \frac{E^2}{c^2 L^2} \]
Isoleren van \(\left(dr/d\lambda\right)^2\) levert:
\[ \left(\frac{dr}{d\lambda}\right)^2 = L^2 \left( \frac{E^2}{c^2 L^2} - \frac{1}{r^2} \left(1 - \frac{2GM}{c^2 r}\right) \right) \tag{16} \]
4.3.3 Impactparameter en impulsmoment
De impactparameter \(b\) is de afstand tussen de zwaartelijn van het massieve object (de zon) en de asymptotische richting van de lichtstraal op oneindig.
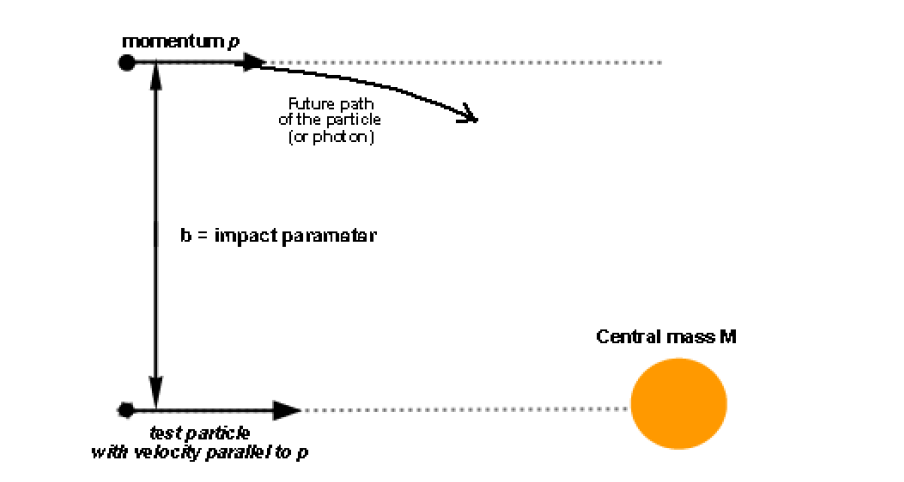
Het impulsmoment van het foton is:
\[ L = p\,b \tag{17} \]
Voor een foton geldt \(E = pc\), zodat:
\[ b = \frac{L}{E/c} \tag{18} \]
Extra verduidelijking van de relatie (17) en (18):
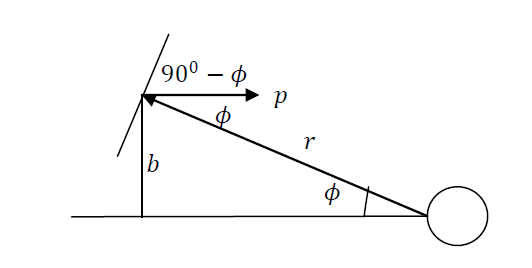
Het impulsmoment is \(𝐿=𝑝 \, \sin\phi\cdot r=p\cdot r\, \sin\phi \)
De energie in het algemeen is \(E^2=p^2 c^2+m^2 c^4 \); en voor een foton geldt \(m=0\), dus \(E=pc\).
Dus:
\[ \frac{L}{E/c}=\frac{pb}{pc/c}=b \]
Hieruit volgt:
\[ \frac{1}{b^2} = \frac{E^2}{c^2 L^2} \tag{18a} \]
4.3.4 Afleiding van het pad: de baanvergelijking voor het foton
Uit de behouden grootheid volgt:
\[ r^2 \frac{d\phi}{d\lambda} = L \]
Dus:
\[ \frac{d\phi}{d\lambda}=\frac{d\phi}{dr}\frac{dr}{d\lambda}=\frac{L}{r^2} \quad \Rightarrow \quad \frac{d\phi}{dr} = \frac{L}{r^2} \left(\frac{dr}{d\lambda}\right)^{-1} \]
Samen met(16) geeft dit:
\[ \frac{d\phi}{dr}=\frac{L}{r^2}\left(\frac{dr}{d\lambda}\right)^{-1}=\pm \, \frac{L}{r^2} \frac{1}{L}\left[\frac{E^2}{c^2L^2}-\frac{1}{r^2}\left(1-\frac{2GM}{c^2r}\right)\right]^{-1/2} \]
Met (18a) wordt dit:
\[ \frac{d\phi}{dr} = \pm \frac{1}{r^2} \left( \frac{1}{b^2} - \frac{1}{r^2} \left(1 - \frac{2GM}{c^2 r}\right) \right)^{-1/2} \tag{19} \]
Dit leidt tot:
\[ \left(\frac{1}{r^2}\frac{dr}{d\phi}\right)^2 = \frac{1}{b^2} - \frac{1}{r^2} \left(1 - \frac{2GM}{c^2 r}\right) \tag{20} \]
4.3.5 De integratie van het pad
De afbuigingshoek wordt verkregen door de hoekverandering \(\Delta \phi\) langs het traject van het foton te berekenen, van oneindig tot aan het perihelium \(r = R\), en weer terug. Vanuit vergelijking (19) krijgen we (zie Figuur 3):
\[ \Delta \phi = 2 \int_{r_1}^{\infty} \frac{dr}{r^2 \sqrt{ \frac{1}{b^2} - \frac{1}{r^2} \left( 1 - \frac{2GM}{c^2 r} \right) }} \tag{21} \]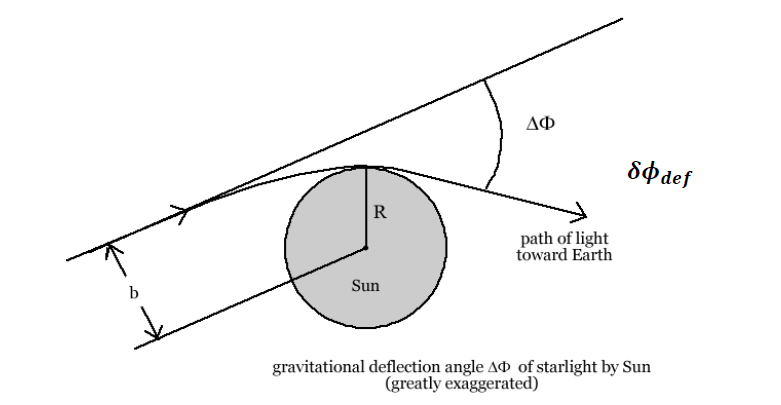
Op het keerpunt \(r = R\) geldt \[ \frac{dr}{d\phi} = 0 \] zodat uit vergelijking (20) volgt:
\[ \frac{1}{b^2} = \frac{1}{R^2} \left( 1 - \frac{2GM}{c^2 R} \right) \tag{22} \]Vervang dit in vergelijking (20):
\[ \left( \frac{1}{r^2} \frac{dr}{d\phi} \right)^2 = \frac{1}{R^2} \left( 1 - \frac{2GM}{c^2 R} \right) - \frac{1}{r^2} \left( 1 - \frac{2GM}{c^2 r} \right) \tag{23} \]4.3.6 Variabele substitutie
Voer de volgende substitutie uit:
\[ u = \frac{R}{r} \]Dan geldt:
\[ \frac{du}{d\phi} = \frac{du}{dr} \frac{dr}{d\phi} = - \frac{R}{r^2} \frac{dr}{d\phi} \] \[ \left( \frac{du}{d\phi} \right)^2 = \frac{R^2}{r^4} \left( \frac{dr}{d\phi} \right)^2 \]Waarbij \(u\) varieert tussen \(1\) (bij \(r = R\)) en \(0\) (bij \(r = \infty\)). Vergelijking (23) wordt dan:
\[ \left( \frac{du}{d\phi} \right)^2 = \left( 1 - \frac{2GM}{c^2 R} \right) - u^2 \left( 1 - \frac{2GM}{c^2 R} u \right) \]Of:
\[ \left( \frac{du}{d\phi} \right)^2 = 1 - u^2 - \frac{2GM}{c^2 R} \left( 1 - u^3 \right) \tag{24} \]Hieruit volgt:
\[ d\phi = \left[ 1 - u^2 - \frac{2GM}{c^2 R} \left( 1 - u^3 \right) \right]^{-1/2} du \] \[ =\frac{\left(1-u^2\right)^{-1/2}}{\left[1-\frac{2GM}{c^2R}\left(1-u^3\right) \left(1-u^2\right)^{-1}\right]^{1/2}}\,du \tag{25} \]Deze integraal is lastig op te lossen in gesloten vorm. Om haar eenvoudiger te maken, gebruiken we de substitutie:
\[ u = \cos \alpha, \qquad 0 < \alpha < \frac{\pi}{2} \quad dus \quad 0 < u < 1 \]Dan wordt:
\[ d\phi = - \left[ 1 - \frac{2GM}{c^2 R} \frac{1 - \cos^3 \alpha}{\sin^2 \alpha} \right]^{-1/2} d\alpha \tag{26} \]Door in te zien dat:
\[ \frac{1 - \cos^3 \alpha}{\sin^2 \alpha} = \frac{(1 - \cos \alpha)(1 + \cos \alpha + \cos^2 \alpha)} {(1 - \cos \alpha)(1 + \cos \alpha)} = \frac{1 + \cos \alpha + \cos^2 \alpha}{1 + \cos \alpha} \] \[ =\frac{1 + \cos \alpha \left(1 + \cos \alpha\right)}{1 + \cos \alpha}=\cos \alpha+\frac{1}{1 + \cos \alpha} \]krijgen we uiteindelijk:
\[ d\phi = - \left[ 1 - \frac{2GM}{c^2 R}\left(\cos\alpha+\frac{1}{1+\cos\alpha}\right) \right]^{-1/2} d\alpha \tag{27} \]Met:
\[ \cos \alpha = \frac{R}{r} \]Tot op dit punt is geen enkele benadering toegepast. Deze volledige afleiding is geschikt om de lichtafbuiging exact te berekenen, al is in de praktijk vaak een eerste-orde benadering voldoende om de afbuigingshoek langs de rand van de zon te bepalen.
4.3.6.1 Benaderingen en integratie
De parameter \[ \frac{2GM}{c^2 R} \approx 4.24 \times 10^{-6} \] is zeer klein aan het oppervlak van de zon.
We passen de Taylor-benadering toe:
\[ \frac{1}{\sqrt{1 - k}} \approx 1 + \frac{1}{2} k \]Toegepast op vergelijking (27) levert dit:
\[ d\phi = - \left[ 1 - \frac{2GM}{c^2 R}\left(\cos\alpha+\frac{1}{1+\cos\alpha}\right) \right]^{-1/2} d\alpha \]Of:
\[ d\phi = -\frac{1}{\sqrt{\left[ 1 - \frac{2GM}{c^2 R}\left(\cos\alpha+\frac{1}{1+\cos\alpha}\right) \right]}}d\alpha \]Na benadering volgt:
\[ d\phi \approx - \left[ 1 + \frac{GM}{c^2 R} \left(\cos \alpha+\frac{1}{1 + \cos \alpha}\right) \right] d\alpha \tag{28} \]We kunnen nu de totale verandering in het azimut berekenen langs het volledige traject van het foton, van \(\alpha=0\) tot \(\alpha=\frac{\pi}{2}\), en dit verdubbelen:
De totale hoekverandering wordt dan:
\[ \Delta \phi = 2 \int_{0}^{\pi/2} \left[ 1 + \frac{GM}{c^2 R} \left(\cos \alpha+\frac{1}{1 + \cos \alpha}\right) \right] d\alpha \tag{29} \] Om deze integraal uit te werken, bekijken we de tweede term apart. We beschouwen de integraal: \[ \int \frac{1}{1+\cos\alpha}\, d\alpha \] We gebruiken de goniometrische identiteit: \[ 1+\cos\alpha = 1 + \cos\left(\frac{\alpha}{2} + \frac{\alpha}{2}\right) = \cos^2\frac{\alpha}{2} + \sin^2\frac{\alpha}{2} + \cos^2\frac{\alpha}{2} - \sin^2\frac{\alpha}{2} = 2\cos^2\frac{\alpha}{2}. \] Dus: \[ \frac{1}{1+\cos\alpha} = \frac{1}{2\cos^2\frac{\alpha}{2}}. \] Merk op dat: \[ \frac{1}{2\cos^2\frac{\alpha}{2}} = \frac{1}{2}\left(1+\frac{\sin^2\frac{\alpha}{2}}{\cos^2\frac{\alpha}{2}} \right) = \frac{1}{2}\left( \frac{\cos\frac{\alpha}{2}}{\cos\frac{\alpha}{2}} + \frac{\sin^2\frac{\alpha}{2}}{\cos^2\frac{\alpha}{2}} \right) = \frac{1}{2}\frac{d}{d(\alpha/2)}\tan\frac{\alpha}{2} = \frac{d}{d\alpha}\left(\tan\frac{\alpha}{2}\right). \] Dus: \[ \int \frac{1}{1+\cos\alpha}\, d\alpha = \tan\frac{\alpha}{2}. \]Nu kunnen we de volledige integraal (29) evalueren::
\[ \Delta \phi = 2 \left[ \alpha + \frac{GM}{c^2 R} \left( \sin \alpha + \tan \frac{\alpha}{2} \right) \right]_{0}^{\pi/2} \tag{30} \] We vullen in: \[ \begin{aligned} \alpha = \frac{\pi}{2}: &\qquad \sin\frac{\pi}{2} = 1,\qquad \tan\frac{\pi}{4} = 1,\\[6pt] \alpha = 0: &\qquad \sin 0 = 0,\qquad \tan 0 = 0. \end{aligned} \] Dus: \[ \Delta\phi = 2\left( \frac{\pi}{2} + \frac{GM}{c^{2}R}(1 + 1) \right) = \pi + \frac{4GM}{c^{2}R}. \] \[ \Delta \phi = \pi + \frac{4GM}{c^2 R} \tag{31} \]Opmerking: de integraal zou van \(r=\infty\) naar R moeten gaan, dus nu gaat \(u\) van 0 naar 1, en dus \(\alpha\) van \(\frac{\pi}{2}\) naar 0. Door de integraal te veranderen naar 0 tot \(\frac{\pi}{2}\) verandert het teken en verdwijnt het minteken.
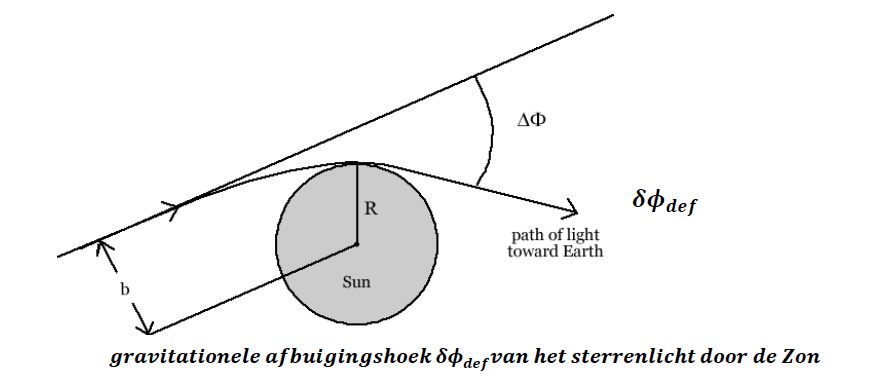
De eerste term, \(\pi\), is de totale hoekverandering van een foton in een vlakke ruimte-tijd – een rechte baan zonder afbuiging. De tweede term is de extra afbuiging ten gevolge van de kromming van de ruimte-tijd. De werkelijke afbuigingshoek is dus:
\[ \delta \phi_{\mathrm{def}} = \Delta \phi - \pi \approx \frac{4GM}{c^2 R} \tag{32} \]Numerieke waarde
Met: \[ \begin{aligned} G &= 6.674 \cdot 10^{-11}\ \mathrm{N\,m^{2}/kg^{2}},\\ M_{\odot} &= 1.989 \cdot 10^{30}\ \mathrm{kg},\\ c &= 3.00 \cdot 10^{8}\ \mathrm{m/s},\\ R_{\odot} &= 6.963 \cdot 10^{8}\ \mathrm{m}, \end{aligned} \] vinden we: \[ \delta\phi_{\mathrm{def}} = \frac{4GM_{\odot}}{c^{2}R_{\odot}} = \frac{4 \cdot 6.674\cdot 10^{-11} \cdot 1.989\cdot 10^{30}} {(3.00\cdot 10^{8})^{2} \cdot 6.963\cdot 10^{8}} \approx 8.5 \cdot 10^{-6}\ \text{radialen}. \] Om dit om te zetten in boogseconden gebruiken we: \[ 1\ \text{rad} = \frac{180 \cdot 60 \cdot 60}{\pi} \approx 206.265''. \] Daaruit volgt: \[ \delta\phi_{\mathrm{def}} \approx 8.5 \cdot 10^{-6} \times 206.265'' \approx 1.75''. \]4.3.7 Conclusie
Deze afbuiging van 1.75 boogseconde werd voor het eerst waargenomen door Arthur Eddington tijdens de zonsverduistering van 1919. Het resultaat bevestigde op spectaculaire wijze Einsteins voorspelling, en betekende een mijlpaal in de experimentele bevestiging van de algemene relativiteitstheorie.
Dit effect is ook te zien buiten ons zonnestelsel, en staat bekend als “gravitational lensing”.
4.3.8 Fysische interpretatie
- Licht volgt de kromming van ruimte-tijd.
- De afbuiging is een geometrisch effect, geen kracht.
- Waarneembaar tijdens zonsverduisteringen.
4.4 Experiment 4 – Precessie van de Periheliën (Mercurius)
Gebaseerd op artikel van Owen Biesel (Biesel, 2008).
4.4.1 Inleiding
- Fysisch probleem: De baan van Mercurius rond de zon is een ellips, maar het dichtstbijzijnde punt (perihelium) schuift langzaam door in de tijd. Dit verschijnsel heet precessie van het perihelium.
- Klassieke verklaring: Newtoniaanse mechanica verklaart het grootste deel van deze precessie (door invloed van andere planeten), maar er blijft een residu van circa 43 boogseconden per eeuw onverklaard.
- Relativistische verklaring: De algemene relativiteitstheorie voorspelt een extra precessie als gevolg van de kromming van ruimte-tijd rond de zon, exact overeenkomend met het waargenomen overschot.
4.4.2 Theoretisch kader: Schwarzschild-metriek
In de algemene relativiteitstheorie beschouwen we een planeet zoals Mercurius als een testdeeltje dat zich langs een geodetische baan beweegt door de gekromde ruimte-tijd.
De Schwarzschild-metriek beschrijft deze ruimte-tijd rondom een sferisch symmetrische massa (zoals de zon):
\[ ds^{2} = c^{2} d\tau^{2} = \sigma^{2} c^{2} dt^{2} - \frac{dr^{2}}{\sigma^{2}} - r^{2} d\theta^{2} - r^{2} \sin^{2}\theta \, d\phi^{2} \tag{33} \]met:
\[ \sigma = \sqrt{1 - \frac{2GM}{c^{2} r}} = \sqrt{1 - \frac{R_{s}}{r}}, \qquad R_{s} = \frac{2GM}{c^{2}} \]Voor een planeet die beweegt in het equatoriale vlak \(\left( \theta = \frac{\pi}{2}\right) \) vereenvoudigt dit tot:
\[ 1 = \left(1 - \frac{R_{s}}{r}\right) \left(\frac{dt}{d\tau}\right)^{2} - \frac{1}{c^{2}} \left(1 - \frac{R_{s}}{r}\right)^{-1} \left(\frac{dr}{d\tau}\right)^{2} - \frac{1}{c^{2}} r^{2} \left(\frac{d\phi}{d\tau}\right)^{2} \]4.4.3 Afleiding via de precessie via de Lagrange-aanpak (zie Appendix 12)
Hoewel we eerder al de uitdrukkingen voor de energie E vergelijking_3.2_9) en het impulsmoment L (vergelijking_3.2_11) hebben afgeleid, herhalen we hier de afleiding vanuit de Lagrangiaan. We parameteriseren de baan als:
\[ x^{\mu}(\tau) = \bigl( t(\tau), r(\tau), \theta(\tau), \phi(\tau) \bigr) \]met \(\tau\) de eigentijd. In het equatoriale vlak \(\theta =\frac{\pi}{2} wordt de Lagrangiaan:
\[ \mathcal{L} = \left(1 - \frac{R_{s}}{r}\right) \left(\frac{dt}{d\tau}\right)^{2} - \frac{1}{c^{2}} \left(1 - \frac{R_{s}}{r}\right)^{-1} \left(\frac{dr}{d\tau}\right)^{2} - \frac{1}{c^{2}} r^{2} \left(\frac{d\phi}{d\tau}\right)^{2} \tag{34} \]De Euler-Lagrange-vergelijkingen voor ∅ en t geven:
\[ \frac{d\phi}{d\tau} = \dot{\phi}, \qquad \frac{dt}{d\tau} = \dot{t}. \]De Lagrangiaan wordt dan:
\[ \mathcal{L} = \left(1 - \frac{R_s}{r}\right)\dot{t}^{\,2} - \frac{1}{c^{2}}\left(1 - \frac{R_s}{r}\right)^{-1}\dot{r}^{\,2} - \frac{1}{c^{2}}\, r^{2}\dot{\phi}^{\,2}. \]4.4.4 Euler–Lagrange-operatie
Hier is voor \( \phi \):
\[ \frac{d}{d\tau}\left( \frac{\partial \mathcal{L}}{\partial \dot{\phi}} \right) = \frac{\partial \mathcal{L}}{\partial \phi} = 0, \]en voor \( t \):
\[ \frac{d}{d\tau}\left( \frac{\partial \mathcal{L}}{\partial \dot{t}} \right) = \frac{\partial \mathcal{L}}{\partial t} = 0. \]Dan gelden de Euler–Lagrange‑vergelijkingen voor \( \phi \) en \( t \):
\[ 0 = \frac{d}{d\tau}\left(2 \frac{1}{c^{2}} r^{2}\frac{d\phi}{d\tau} \right) \quad\Rightarrow\quad r^{2}\frac{d\phi}{d\tau} = \text{constant} = L, \] \[ 0 = \frac{d}{d\tau}\left[ 2\left(1 - \frac{R_s}{r}\right)\frac{dt}{d\tau} \right] \quad\Rightarrow\quad \left(1 - \frac{R_s}{r}\right)\frac{dt}{d\tau} = \text{constant} = \frac{E}{c^{2}}. \]Hieruit volgt dat \( L \) (het impulsmoment per eenheid massa) en \( E \) (de energie per eenheid massa) bewegingsconstanten zijn.
We herschrijven de oorspronkelijke normvoorwaarde.
De normvoorwaarde luidt:
\[ 1 = \left(1 - \frac{R_s}{r}\right)\left(\frac{dt}{d\tau}\right)^{2} - \frac{1}{c^{2}}\left(1 - \frac{R_s}{r}\right)^{-1}\left(\frac{dr}{d\tau}\right)^{2} - \frac{1}{c^{2}} r^{2}\left(\frac{d\phi}{d\tau}\right)^{2}. \]We substitueren de constanten \(E\) en \(L\):
\[ 1 = \frac{\frac{E^{2}}{c^{4}}}{1-\frac{R_s}{r}} - \frac{1}{c^{2}}\frac{\left(\frac{dr}{d\tau}\right)^{2}}{1 - \frac{R_s}{r}} - \frac{L^{2}}{c^{2} r^{2}}. \] \[ 1 - \frac{R_s}{r} = \frac{E^{2}}{c^{4}} - \frac{1}{c^{2}}\left(\frac{dr}{d\tau}\right)^{2} - \frac{L^{2}}{c^{2}r^{2}} + \frac{R_s L^{2}}{c^{2} r^{3}}. \]Dus:
\[ \left(\frac{dr}{d\tau}\right)^{2} = c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right) + c^{2}\frac{R_s}{r} - \frac{L^{2}}{r^{2}} + \frac{R_s L^{2}}{r^{3}}. \]Door:
\[ \frac{dr}{d\tau} = \frac{dr}{d\tau} = \frac{dr}{d\phi}\frac{d\phi}{d\tau} = \frac{dr}{d\phi}\frac{L}{r^{2}} \quad\Rightarrow\quad \left(\frac{dr}{d\phi}\right)^{2} = \frac{r^{4}}{L^{2}}\,\left(\frac{dr}{d\tau}\right)^{2}, \]verkrijgen we:
\[ \left(\frac{dr}{d\phi}\right)^{2} = \frac{r^{4}}{L^{2}} \left[ c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right) + c^{2}\frac{R_s}{r} - \frac{L^{2}}{r^{2}} + \frac{R_s L^{2}}{r^{3}} \right]. \]Dit kunnen we schrijven als:
\[ \left(\frac{dr}{d\phi}\right)^{2} = \text{Newtonse termen} \;+\; \text{relativistische correctie}. \]De extra term \( \frac{R_s L^{2}}{r^{3}} \) in de effectieve potentiaal veroorzaakt de precessie van het perihelium.
Na vereenvoudiging:
\[ \left(\frac{dr}{d\phi}\right)^{2} = \frac{c^{2}}{L^{2}}\left(\frac{E^{2}}{c^{4}} - 1\right) r^{4} + \frac{c^{2}R_s}{L^2} r^{3} - r^{2} + R_s r. \]Hieruit leiden we af:
\[ d\phi = \frac{dr}{ \sqrt{ \frac{c^{2}}{L^{2}}\left(\frac{E^{2}}{c^{4}} - 1\right) r^{4} + \frac{c^{2}R_s}{L^2} r^{3} - r^{2} + R_s r }}. \]4.4.5 Precessie van de baan
Voor een gesloten baan moet de radiale beweging begrensd zijn, d.w.z. \(dr/d\phi=0\) bij twee punten: het perihelium P en het aphelium A. Maar bij een niet gesloten baan (precessie) is de hoekverschuiving tussen perihelium \(P\) en aphelium \(A\):
\[ \phi_{A} - \phi_{P} = \int_{P}^{A} \frac{dr}{ \sqrt{ \frac{c^{2}}{L^{2}} \left(\frac{E^{2}}{c^{4}} - 1\right) r^{4} + \frac{c^{2} R_{s}}{L^2} r^{3} - r^{2} + R_{s} r } } \tag{35} \]Om \(E\) en \(L\) in termen van \(A\), \(P\) en \(R_s\) uit te drukken, stellen we dat \(\frac{dr}{d\phi}=0\) voor \(r=A\) en \(r=P\). Dit leidt tot de volgende vergelijkingen:
\[ c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right)A^{4} + L^{2}(- A^{2}+ R_{s}A) = -c^{2}R_{s}A^{3} \tag{36} \] \[ c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right)P^{4} + L^{2}(- P^{2}+ R_{s}P) = -c^{2}R_{s}P^{3} \tag{37} \]Door geschikte combinaties en aftrekkingen van deze vergelijkingen kunnen we \(\frac{E^{2}}{c^{4}} - 1\) en \(L^{2}\) volledig uitdrukken in termen van \(A\), \(P\) en \(R_s\). (Details zie oorspronkelijke afleiding.)
Vermenigvuldig (36) met \((-P^{2}+R_{s}P)\):
\[ c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right)A^{4}(-P^{2}+R_{s}P) + L^{2}(-A^{2}+R_{s}A)(-P^{2}+R_{s}P) = -c^{2}R_{s}A^{3}(-P^{2}+R_{s}P) \]Vermenigvuldig (37) met \((-A^{2}+R_{s}A)\):
\[ c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right)P^{4}(-A^{2}+R_{s}A) + L^{2}(-P^{2}+R_{s}P)(-A^{2}+R_{s}A) = -c^{2}R_{s}P^{3}(-A^{2}+R_{s}A) \]Trek deze twee vergelijkingen van elkaar af:
\[ c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right) \left[ A^{4}(-P^{2}+R_{s}P) - P^{4}(-A^{2}+R_{s}A) \right] = -c^{2}R_{s}A^{3}(-P^{2}+R_{s}P) + c^{2}R_{s}P^{3}(-A^{2}+R_{s}A) \]Daaruit volgt:
\[ c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right) = \frac{ -c^{2}R_{s}A^{3}(-P^{2}+R_{s}P) + c^{2}R_{s}P^{3}(-A^{2}+R_{s}A) }{ A^{4}(-P^{2}+R_{s}P) - P^{4}(-A^{2}+R_{s}A) } \]Dus:
\[ \frac{E^{2}}{c^{4}} - 1 = \frac{ -R_{s}A^{3}(-P^{2}+R_{s}P) + R_{s}P^{3}(-A^{2}+R_{s}A) }{ [A^{4}(-P^{2}+R_{s}P) - P^{4}(-A^{2}+R_{s}A)] } \] \[ \frac{E^{2}}{c^{4}} - 1 = \frac{ -R_{s}[A^{3}(-P^{2}+R_{s}P) - P^{3}(-A^{2}+R_{s}A) }{ [A^{4}(-P^{2}+R_{s}P) - P^{4}(-A^{2}+R_{s}A)] } \] \[ \frac{E^{2}}{c^{4}} - 1 = \frac{ -R_{s}[A^{3}P(-P+R_{s}) - P^{3}A(-A+R_{s}) }{ [A^{4}P(-P+R_{s}) - P^{4}A(-A+R_{s})] } \] \[ \frac{E^{2}}{c^{4}} - 1 = \frac{ -R_{s}AP[A^{2}(-P+R_{s}) - P^{2}(-A+R_{s}) }{ AP[A^{3}(-P+R_{s}) - P^{3}(-A+R_{s})] } \] \[ \frac{E^{2}}{c^{4}} - 1 = \frac{ -R_{s}[A^{2}(-P+R_{s}) - P^{2}(-A+R_{s}) }{ [A^{3}(-P+R_{s}) - P^{3}(-A+R_{s})] } \] \[ \frac{E^{2}}{c^{4}} - 1 = \frac{ -R_{s}[-PA^{2}+R_{s}A^{2}+AP^2-R_sP^2] }{ [-PA^{3}+R_sA^3+AP^3-R_sP^3] } \] \[ \frac{E^{2}}{c^{4}} - 1 = \frac{ -R_{s}[-AP(A-P)+R_s(A^2-P^2] }{ [-AP(A^2-P^2)+R_s(A^3-P^3] } \] \[ \frac{E^{2}}{c^{4}} - 1 = \frac{ -R_{s}(A-P)[-AP+R_s(A+P] }{ (A-P)[-AP(A+P)+R_s\frac{(A^3-P^3}{A-P}] } \]Intermezzo om \(\frac{(A^3-P^3}{A-P}\) uit te werken: \[ (A^2-P^2)(A+P)=A^3-AP^2+A^2P-P^3 \] \[ A^3-P^3=(A^2-P^2)(A+P)-AP(A-P) \] \[ A^3-P^3=(A-P)(A+P)(A+P)-AP(A-P) \] \[ \Rightarrow\quad \frac{A^3-P^3}{A-P}=(A+P)^2-AP \]
Nu vullen we het resultaat in: \[ \frac{E^{2}}{c^{4}} - 1 = \frac{ -R_{s}(A-P)[-AP+R_s(A+P] }{ (A-P)[-AP(A+P)+R_s(A+P)^2-R_sAP] } \] \[ \frac{E^{2}}{c^{4}} - 1 = \frac{ -R_{s}[-AP+R_s(A+P] }{ [-AP(A+P+R_s)+R_s(A+P)^2] } \] \[ \frac{E^{2}}{c^{4}} - 1 = \frac{ R_{s}[-AP+R_s(A+P] }{ [AP(A+P+R_s)-R_s(A+P)^2] } \tag{36a} \]
Nu kunnen we \(L^2/c^2\) vinden door dezelfde methode toe te passen op vergelijkingen (36) en (37):
\[ c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right)A^{4} + L^{2}(- A^{2}+ R_{s}A) = -c^{2}R_{s}A^{3} \tag{36} \] \[ c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right)P^{4} + L^{2}(- P^{2}+ R_{s}P) = -c^{2}R_{s}P^{3} \tag{37} \]Vermenigvuldig (37) met \(A^4\):
\[ c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right)A^4P^{4} + L^{2}(- P^{2}+ R_{s}P)A^4 = -c^{2}R_{s}A^4P^{3} \]Nu aftrekken:
\[ L^{2}[(-A^2+R_sA)P^4-(-P^2+R_sP)A^4]=-c^2R_sA^3P^4+c^2R_sA^4P^3 \] \[ L^2=\frac{c^2R_sA^3P^3(-P+A)}{(-A^2+R_sA)P^4-(-P^2+R_sP)A^4} \] \[ L^2=\frac{c^2R_sA^3P^3(-P+A)}{(-A+R_s)AP^4-(-P+R_s)PA^4} \] \[ L^2=\frac{c^2R_sA^3P^3(-P+A)}{AP[(-A+R_s)P^3-(-P+R_s)A^3} \] \[ L^2=\frac{c^2R_sA^2P^2(-P+A)}{[(-A+R_s)P^3-(-P+R_s)A^3} \] \[ L^2=\frac{c^2R_sA^2P^2(-P+A)}{A^3P-AP^3-(A^3-P^3)R_s} \] \[ L^2=\frac{c^2R_sA^2P^2(-P+A)}{AP(A^2-P^2)-(A^3-P^3)R_s} \] \[ L^2=\frac{c^2R_sA^2P^2}{AP(A+P)-R_s(A+P)^2+APR_s} \] \[ L^2=\frac{c^2R_sA^2P^2}{AP(A+P+R_s)-R_s(A+P)^2} \] \[ \frac{L^2}{c^2}=\frac{R_sA^2P^2}{AP(A+P+R_s)-R_s(A+P)^2} \]Uiteindelijk krijgen we de vergelijking (36a) van boven en de vergelijking van \(L^2/c^2\):
\[ \frac{E^2}{c^4}-1=\frac{-APR_s+(A+P)R_s^2}{AP(A+P+R_s)-R_s(A+P)^2} \] \[ \frac{L^2}{c^2}=\frac{A^2P^2R_s}{AP(A+P+R_s)-R_s(A+P)^2} \]Vervolgens kunnen we de variabele: \[ D=\frac{AP}{A+P} \]
introduceren om de uitdrukkingen verder te vereenvoudigen. Dit heeft de dimensie van afstand. Dan wordt de uitdrukking hierboven voor \(E^2-1\) en \(L^2\):
We hadden eerder gevonden:
\[ \frac{E^{2}}{c^{4}} - 1 =\frac{ -\frac{R_{s}}{AP} + \frac{R_{s}^{2}}{D\,AP})} { \frac{1}{D} + \frac{R_{s}}{AP} - \frac{R_{s}}{D^{2}} } \] \[ \frac{L^{2}}{c^{2}} = \frac{R_{s}}{ \frac{1}{D} + \frac{R_{s}}{AP} - \frac{R_{s}}{D^{2}}} \]Daarmee geldt:
\[ \frac{\frac{L^{2}}{c^{2}}}{ \frac{E^{2}}{c^{4}} - 1 } = \frac{R_{s}}{ -\frac{R_{s}}{AP} + \frac{R_{s}^{2}}{D\,AP} } = \frac{AP}{- 1 + R_{s}/D} \] \[\frac{ \frac{L^{2}}{c^{2}AP}}{{1 - \frac{E^{2}}{c^{4}}}} = \frac{1}{1 - R_{s}/D} \tag{38} \]We willen een uitdrukking voor \(\varepsilon\), de derde niet-nul wortel van:
\[ \frac{E^{2}/c^{4} - 1}{L^{2}/c^{2}} r^{4} + \frac{R_{s}}{L^2/c^2} r^{3} - r^{2} + R_{s} r = 0 \] \[ \frac{E^2/c^4-1}{L^2/c^2}\left[r^4+\frac{R_s}{E^2/c^4-1}r^3- \frac{L^2/c^2}{E^2/c^4-1}r^2+\frac{L^2/c^2}{E^2/c^4-1}R_sr \right]=0 \]Dit geeft dus de drie niet-nul wortels: A, P and \(\varepsilon\).
De volledige uitdrukking wordt:
\[ \frac{E^2/c^4-1}{L^2/c^2} (r-A)(r-P)(r-\varepsilon) r \]Laten we de vier factoren uitwerken:
\[ \frac{E^2/c^4-1}{L^2/c^2}\left[ r^{4} - (A+P+\varepsilon)\, r^{3} + \{AP + \varepsilon(A + P)\}\, r^{2} - \varepsilon AP\, r \right] \]We weten dat de som van de drie niet-nul wortels gelijk is aan \(\dfrac{R_{s}}{E^{2}/c^{4} - 1}\) (de coëfficiënt van \(r^{3}\) in de standaardvorm van het polynoom); daarom verkrijgen we:
\[ -(A+P+\varepsilon) = \frac{R_{s}}{E^{2}/c^{4} - 1} \]Dit stelt ons in staat om de relatie tussen de wortels A, P en \(\varepsilon\) verder te analyseren in termen van \(R_{s}\), de Schwarzschildstraal, en de energie- en impulsmomenttermen.
Uit bovenstaande weten we dat:
\[ \frac{E^2}{c^4}-1=\frac{R_s[-AP+(A+P)R_s]}{AP(A+P+R_s)-R_s(A+P)^2} \]Dus we vullen dit in de bovenstaande vergelijking:
\[ A + P + \varepsilon = \frac{R_{s}}{E^{2}/c^{4} - 1} \] \[ A + P + \varepsilon = R_s\frac{-AP(A+P+R_s)+R_s(A+P)^2}{R_s[-AP+(A+P)R_s]}=\frac{-AP(A+P+R_s)+R_s(A+P)^2}{-AP+(A+P)R_s} \] \[ \varepsilon=\frac{-AP(A+P+R_s)+R_s(A+P)^2}{-AP+(A+P)R_s}-(A+P) \] \[ =\frac{-AP(A+P+R_s)+R_s(A+P)^2+AP(A+P)-(A+P)^2R_s}{-AP+(A+P)R_s} \] \[ \varepsilon=\frac{-AP(A+P+R_s)+AP(A+P)}{-AP+(A+P)R_s}=\frac{-APR_s}{-AP+(A+P)R_s}= \frac{R_s}{1-\frac{(A+P)R_s}{AP}}=\frac{R_s}{1-\frac{R_s}{D}} \]Wat geeft:
\[ \varepsilon = R_{s}\left(1 - \frac{R_{s}}{D}\right) \tag{39} \]Nu kunnen we (35) benaderen door te schrijven
\[ \frac{E^2/c^4-1}{L^2/c^2}r^4 + \frac{R_s}{L^2/c^2}r^3-r^2+R_s r =\frac{E^2/c^4-1}{L^2/c^2} (r-A)(r-P)(r-\varepsilon) r \] \[ =\frac{1-E^2/c^4}{L^2/c^2} (A-r)(r-P)(r-\varepsilon) r \]We verkrijgen met behulp van vergelijking (35):
\[ \phi_{A} - \phi_{P} = \sqrt{\frac{L^{2}/c^{2}}{1 - E^{2}/c^{4}}} \int_{P}^{A} \frac{1}{\sqrt{r(A-r)(r-P)(r-\varepsilon)}}\,dr \] \[ = \sqrt{\frac{L^{2}/c^{2}}{1 - E^{2}/c^{4}}} \int_{P}^{A} \frac{1}{\sqrt{r^2(A-r)(r-P)(1-\frac{\varepsilon}{r})}}\,dr \] \[ = \sqrt{\frac{L^{2}/c^{2}}{1 - E^{2}/c^{4}}} \int_{P}^{A} \frac{1}{r\sqrt{(A-r)(r-P)}}(1-\frac{\varepsilon}{r})^{-1/2}\,dr \]Nu gebruiken we de Taylorreeksontwikkeling
\[ (1-\frac{\varepsilon}{ r})^{-1/2} \approx 1 + \frac{\varepsilon}{2 r}, \]met een fout \(\varepsilon\) begrensd door:
\[ |\varepsilon| \leq \frac{3}{8}(1-\frac{\varepsilon}{ r})^{-5/2}(\frac{\varepsilon}{ r})^{2} \leq \frac{3}{8}(1-\frac{\varepsilon}{ A})^{-5/2}(\frac{\varepsilon}{ P})^{2} \]wat produceert:
\[ \phi_{A} - \phi_{P} = \sqrt{\frac{L^{2}/c^{2}}{1 - E^{2}/c^{4}}} \int_{P}^{A}\left[\frac{1}{r\sqrt{(A-r)(r-P)}} +\frac{\varepsilon/2}{r^2\sqrt{(A-r)(r-P)}} \right]dr \tag{40} \]Opmerking:
In zijn artikel “The Precession of Mercury’s Perihelion” van Owen Biesel (25 januari 2008), op pagina 8,
bevat het linkerdeel van de integraal (40) in de teller \(1+\varepsilon\), maar wij zijn van mening dat het alleen \(1\) moet zijn en hebben de formule dienovereenkomstig aangepast.
De eerste integraal van (40) (uitwerking zie 4.4.6.1 en 4.4.6.3) in gesloten vorm:
\[ \int_{P}^{A} \frac{1}{r\sqrt{(A-r)(r-P)}}\,dr \] \[ =\frac{1}{\sqrt{AP}}\arctan{\left[ \frac{(A-r)(r-P)+r^2-AP}{2\sqrt{(A-r)(r-P)AP}} \right]_{P}^{A}} \] \[ \to \frac{1}{\sqrt{AP}} \left[ \arctan(+\infty) - \arctan(-\infty) \right] = \frac{1}{\sqrt{AP}} \left( \frac{\pi}{2} + \frac{\pi}{2} \right) = \frac{\pi}{\sqrt{AP}} \]De tweede integraal van (40) (uitwerking zie 4.4.6.2) is lastiger, maar kan in gesloten vorm worden geëvalueerd:
\[ \int_P^A \frac{\varepsilon/2}{r^2\sqrt{(A-r)(r-P)}}\,dr = \frac{\pi \varepsilon/2}{2\sqrt{AP}}\frac{A+P}{AP} = \frac{1}{\sqrt{AP}}\frac{\pi \varepsilon}{4D} \]Als we nu herkennen dat:
\[ \frac{L^{2}}{c^{2}}\frac{AP}{1 - E^{2}/c^{4}} = \frac{1}{1 - R_{s}/D} \]en:
\[ \varepsilon = \frac{R_{s}}{1 - R_{s}/D} \](zie (38) en (39) hierboven), dan vinden we dat:
\[ \phi_{A} - \phi_{P} = \frac{1}{\sqrt{AP}}\pi \sqrt{\frac{L^{2}/c^{2}}{1 - E^{2}/c^{4}}} + \frac{1}{\sqrt{AP}}\frac{\pi \varepsilon}{4D}\sqrt{\frac{L^{2}/c^{2}}{1 - E^{2}/c^{4}}} \] \[ \phi_{A} - \phi_{P} = \pi \sqrt{\frac{L^{2}/c^{2}}{AP(1 - E^{2}/c^{4})}} + \frac{\pi\varepsilon}{4D}\sqrt{\frac{L^{2}/c^{2}}{AP(1 - E^{2}/c^{4})}} \] \[ \phi_{A} - \phi_{P} = \pi \sqrt{\frac{1}{1 - R_{s}/D}} + \frac{\pi\varepsilon}{4D}\sqrt{\frac{1}{1 - R_{s}/D}} \] \[ = \frac{\pi}{\sqrt{1 - R_{s}/D}} \left( 1 + \frac{\varepsilon}{4D} \right) \] \[ = \frac{\pi}{\sqrt{1 - R_{s}/D}} \left( 1 + \frac{1}{4D}\frac{R_{s}}{1 - R_{s}/D} \right) \] \[ = \frac{\pi}{\sqrt{1 - R_{s}/D}} \left( 1 + \frac{1}{4}\frac{R_{s}/D}{1 - R_{s}/D} \right) \]Met de waargenomen waarden \(A\text{(aphelion)} = 69.8 \cdot 10^{6}\,\text{km}\), en \(P\text{(perihelion)} = 46.0 \cdot 10^{6}\,\text{km}\), verkrijgen we:
\[ D = 27.7 \cdot 10^{6}\,\text{km}, \qquad R_{s} = \frac{2GM}{c^{2}} = 2.95\,\text{km} \]En kunnen we de term als volgt benaderen:
\[ \frac{\pi}{\sqrt{1 - R_{s}/D}} \left( 1 + \frac{1}{4}\frac{R_{s}/D}{1 - R_{s}/D} \right) \approx \pi + 2.512 \cdot 10^{-7} \]Dit levert een betrouwbare schatting van \(\phi_{A} - \phi_{P}\) op (een halve omwenteling, in radialen).
Dit geeft:
\[ \Delta \phi = 2.512 \cdot 10^{-7} \text{ radialen (halve omwenteling)} \]En:
\[ \Delta \phi = 5.024 \cdot 10^{-7} \text{ radialen (hele omwenteling)} \]De omlooptijd van Mercurius is 87,969 dagen, dus Mercurius voltooit 415,2 omwentelingen per eeuw. Aangezien er \( 360 \cdot 60 \cdot 60/2\pi \) boogseconden per radiaal zijn, vinden we dat het perihelium van Mercurius verschuift met:
\[ \Delta \phi = 5.024 \cdot 10^{-7} \cdot \frac{360 \cdot 60 \cdot 60}{2\pi} \cdot 415.2 = 43.027 \text{ boogseconden per eeuw} \] \[ \Delta \phi = \mathbf{43.027\ boogseconden\ per\ eeuw.} \]Opmerking:
Volgens Asaf Pe'er, voor een kleine afbuigingshoek, geeft het resultaat (zie vergelijking 6 hoofdstuk 4.7):
\[ \delta \phi_{\text{prec}} = \frac{6\pi G M_{\text{sun}}}{c^{2} a (1 - \varepsilon^{2})} \tag{41} \]Waarbij voor Mercurius:
- \(a\) is de halve lange as: \(5.79 \times 10^{10}\,\text{m}\)
- \(\varepsilon\) is de excentriciteit: \(0.206\)
- \(M\) is de massa van de zon: \(1.989 \times 10^{30}\,\text{kg}\)
- \(G\) is de gravitatieconstante: \(6.674 \times 10^{-11}\,\text{Nm}^{2}\text{kg}^{-2}\)
- \(c\) is de lichtsnelheid: \(3 \times 10^{8}\,\text{m/s}\)
Om de precessie per eeuw te berekenen:
\[ \Delta \phi = 5.02 \times 10^{-7} \cdot 100 \cdot 365.2588 \cdot \frac{360 \cdot 60 \cdot 60}{2\pi} \] \[ \Delta \phi = \mathbf{43''} \text{ boogseconden per eeuw.} \]Wat dus tot hetzelfde resultaat leidt.
Dit geeft ons de exacte relatie voor de precessiehoek van de baan van Mercurius, zoals beschreven in het resultaat van 43.027 boogseconden per eeuw.
4.4.6 Conclusie
De afwijking van de baan van Mercurius als gevolg van algemene relativiteit wordt bepaald door de extra krommingstermen in vergelijking (35). De feitelijke precessie per omloop kan worden berekend door de afwijking van de integraal \(\Delta \phi\) ten opzichte van \(2\pi\). Deze theoretische voorspelling komt overeen met de waargenomen afwijking van ongeveer 43 boogseconden per eeuw, een effect dat niet door Newtoniaanse mechanica verklaard kan worden.
4.4.6.1 We controleren de eerste integraal
Controle van de integrand:
\[ \frac{d}{dr} \left[ \frac{1}{\sqrt{AP}} \arctan \left( \frac{(A - r)(r - P)+r^2-AP} {2\sqrt{(A-r)(r-P)AP}} \right) \right] \stackrel{?}{=} \frac{1}{r\sqrt{(A - r)(r - P)}} \]We weten dat:
\[ \frac{d}{dx} \arctan x = \frac{1}{1 + x^{2}} \]Daarom:
\[ \frac{1}{\sqrt{AP}}\frac{d}{dr} \left[ \arctan\left(\frac{(A-r)(r-P)+r^2-AP}{2\sqrt{(A-r)(r-P)AP}}\right) \right] \] \[ = \frac{1}{\sqrt{AP}} \frac{1}{1+\left(\frac{(A-r)(r-P)+r^2-AP}{2\sqrt{(A-r)(r-P)AP}}\right)^2} \frac{d}{dr} \left[\frac{(A-r)(r-P)+r^2-AP}{2\sqrt{(A-r)(r-P)AP}}\right] \] \[ = \frac{1}{\sqrt{AP}} \frac{4(A-r)(r-P)AP}{4(A-r)(r-P)AP+[(A-r)(r-P)+r^2-AP]^2} \frac{d}{dr} \left[\frac{(A-r)(r-P)+r^2-AP}{2\sqrt{(A-r)(r-P)AP}}\right] \] \[ \begin{aligned} &=\frac{1}{\sqrt{AP}} \frac{4(A-r)(r-P)AP}{4(A-r)(r-P)AP+[(A-r)(r-P)+r^2-AP]^2}\cdot \\[6pt] &\quad \left[\frac{-(r-P)+(A-r)+2r}{2\sqrt{(A-r)(r-P)AP}} -\frac{AP{(A-r)(r-P)+r^2-AP}{-(r-P)+(A-r)}}{4{(A-r)(r-P)AP}^{3/2}}\right] \end{aligned} \] \[ \begin{aligned} &=\frac{1}{\sqrt{AP}} \frac{4(A-r)(r-P)AP}{4(A-r)(r-P)AP+[(A-r)(r-P)+r^2-AP]^2}\cdot \\[6pt] &\quad \left[\frac{A+P}{2\sqrt{(A-r)(r-P)AP}} -\frac{AP{(A-r)(r-P)+r^2-AP}{-(r-P)+(A-r)}}{4{(A-r)(r-P)AP}^{3/2}}\right] \end{aligned} \] \[ \begin{aligned} &=\frac{1}{\sqrt{AP}} \frac{4(A-r)(r-P)AP}{4(A-r)(r-P)AP+[(A-r)(r-P)+r^2-AP]^2}\cdot \\[6pt] &\quad \left[\frac{A+P}{2\sqrt{(A-r)(r-P)AP}} -\frac{AP{(Ar-2AP+rP)(P+A-2r)}}{4[{(A-r)(r-P)AP}]^{3/2}}\right] \end{aligned} \] \[ \begin{aligned} &=\frac{1}{\sqrt{AP}} \frac{4(A-r)(r-P)AP}{4(A-r)(r-P)AP+[(A-r)(r-P)+r^2-AP]^2}\frac{1}{\sqrt{(A-r)(r-P)AP}}\cdot \\[6pt] &\quad \left[\frac{2(A+P)}{4} -\frac{AP{(Ar-2AP+rP)(P+A-2r)}}{4(A-r)(r-P)AP}\right] \end{aligned} \] \[ \begin{aligned} &=\frac{1}{\sqrt{AP}} \frac{4(A-r)(r-P)AP}{4(A-r)(r-P)AP+[(A-r)(r-P)+r^2-AP]^2}\frac{1}{\sqrt{(A-r)(r-P)AP}}\cdot \\[6pt] &\quad \left[\frac{2(A+P)(A-r)(r-P)AP-AP(Ar-2AP+rP)(P+A-2r)}{4(A-r)(r-P)AP} \right] \end{aligned} \] \[ =\frac{1}{\sqrt{AP}} \frac{2(A+P)(A-r)(r-P)AP-AP(Ar-2AP+rP)(P+A-2r)}{4(A-r)(r-P)AP+[(A-r)(r-P)+r^2-AP]^2} \frac{1}{\sqrt{(A-r)(r-P)AP}} \] \[ =\frac{1}{AP\sqrt{(A-r)(r-P)}} \frac{2(A+P)(A-r)(r-P)AP-AP(Ar-2AP+rP)(P+A-2r)}{4(A-r)(r-P)AP+[(A-r)(r-P)+r^2-AP]^2} \] \[ =\frac{1}{\sqrt{(A-r)(r-P)}} \frac{2(A+P)(A-r)(r-P)-(Ar-2AP+rP)(P+A-2r)}{4(A-r)(r-P)AP+[(A-r)(r-P)+r^2-AP]^2} \] \[ =\frac{1}{\sqrt{(A-r)(r-P)}} \frac{(2A^2-2Ar+2AP-2Pr)(r-P)-(APr-2AP^2+rP^2+A^2r-2A^2P+APr-2Ar^2+4APr-2Pr^2)} {4A^2Pr-4APr^2-4A^2P^2+4AP^2r+[Ar-r^2-AP+Pr+r^2-AP]^2} \] \[ =\frac{1}{\sqrt{(A-r)(r-P)}} \frac{(2A^2-2Ar+2AP-2Pr)(r-P)-(6APr-2AP^2+P^2r+A^2r-2A^2P-2Ar^2-2Pr^2)} {4A^2Pr-4APr^2-4A^2P^2+4AP^2r+[Ar-2AP+Pr]^2} \] \[ =\frac{1}{\sqrt{(A-r)(r-P)}} \frac{2A^2-2Ar+4APr-2Pr^2-2A^2P-2AP^2+2P^2r-6APr+2AP^2-P^2r-A^2r+2A^2P+2Ar^2+2Pr^2} {4A^2Pr-4APr^2-4A^2P^2+4AP^2r+[Ar-2AP+Pr]^2} \] \[ =\frac{1}{\sqrt{(A-r)(r-P)}} \frac{A^2r-2APr+P^2r} {4A^2Pr-4APr^2-4A^2P^2+4AP^2r+[Ar-2AP+Pr]^2} \] \[ =\frac{1}{\sqrt{(A-r)(r-P)}} \frac{r(A^2-2AP+P^2)} {4A^2Pr-4APr^2-4A^2P^2+4AP^2r+[Ar-2AP+Pr]^2} \] \[ =\frac{1}{\sqrt{(A-r)(r-P)}} \frac{r(A-P)^2} {4A^2Pr-4APr^2-4A^2P^2+4AP^2r+A^2r^2+4A^2P^2+P^2r^2-4A^2Pr+2APr^2-4AP^2r} \] \[ =\frac{1}{\sqrt{(A-r)(r-P)}} \frac{r(A-P)^2} {-2APr^2+A^2r^2+P^2r^2} =\frac{1}{\sqrt{(A-r)(r-P)}} \frac{r(A-P)^2} {r^2(-2AP+A^2+P^2)} \]Dit wordt uiteindelijk:
\[ =\frac{1}{\sqrt{(A-r)(r-P)}} \frac{r(A-P)^2} {r^2(A-P)^2} \]Wat resulteert in:
\[ =\frac{1}{r\sqrt{(A-r)(r-P)}} \]Daarom volgt, na expliciete uitwerking en vereenvoudiging, uiteindelijk dat:
\[ \frac{d}{dr} \left[ \frac{1}{\sqrt{AP}} \arctan \left( \frac{(A - r)(r - P)+r^2-AP} {2\sqrt{(A-r)(r-P)AP}} \right) \right] = \frac{1}{r\sqrt{(A - r)(r - P)}} \]Dit betekent dus dat deze vergelijking correct is.
4.4.6.2 Uitwerking van de tweede integraal
We hebben de uitdrukking voor de tweede integraal afgeleid:
De algemene vorm luidt:
\[ \int \frac{1}{x^{2}} \sqrt{a x^{2} + b x + c} \, dx = - \frac{\sqrt{a x^{2} + b x + c}}{c x} - \frac{b}{2c} \int \frac{dx}{\sqrt{a x^{2} + b x + c}} \](Zie ook het volgende hoofdstuk voor de uitwerking van de integraal aan de rechterkant.)
\[ \int \frac{1}{x^{2}} \sqrt{a x^{2} + b x + c} \, dx = - \frac{\sqrt{a x^{2} + b x + c}}{c x} - \frac{b}{2c\sqrt{-c}}\arcsin{\frac{bx+2c}{|x|\sqrt{b^{2} -4ac}}}\, ,(c<0) \]Nu met \[ a = -1, \quad b = A + P, \quad c = -AP \] geldt:
\[ \phi_A - \phi_P =\int_P^A \frac{\varepsilon/2}{r^2\sqrt{(A - r)(r - P)}} \, dr = \int_P^A \frac{\varepsilon/2}{r^2\sqrt{(-r^2+(A+P)r-AP}} \, dr \] \[ = -\varepsilon/2 \left[ \frac{\sqrt{-r^2+(A+P)r-AP}}{-APr} \right]_{P}^{A} +\varepsilon/2\frac{A+P}{2AP\sqrt{AP}} \left[ \arcsin \left( \frac{(A+P)r - 2AP} {|r| \sqrt{(A+P)^2 - 4AP}} \right) \right]_P^A \] \[ = 0 + \frac{\varepsilon}{2} \frac{A+P}{2AP\sqrt{AP}} \left[ \arcsin \left( \frac{(A+P)A - 2AP} {|A|\sqrt{(A+P)^2 - 4AP}} \right) - \arcsin \left( \frac{(A+P)P - 2AP} {|P| \sqrt{(A+P)^2 - 4AP}} \right) \right] \] \[ = \frac{\varepsilon}{2} \frac{A+P}{2AP\sqrt{AP}} \left[ \arcsin \left( \frac{(A-P)A}{|A|(A-P)} \right) - \arcsin \left( \frac{(P-A)P}{|P|(A-P)} \right) \right] \] \[ = \frac{\varepsilon}{2} \frac{A+P}{2AP\sqrt{AP}} \left[ \arcsin(1) - \arcsin(-1) \right] \] \[ = \frac{\varepsilon}{2} \frac{A+P}{2AP\sqrt{AP}} \left( \frac{\pi}{2} - \left(-\frac{\pi}{2}\right) \right) \] \[ = \frac{\varepsilon}{2} \frac{\pi(A+P)}{2AP\sqrt{AP}} = \frac{\pi \varepsilon}{4D\sqrt{AP}} \]Dus:
\[ \phi_{A} - \phi_{P} = \frac{\pi \varepsilon}{4D\sqrt{AP}} \]Dit komt exact overeen met de eerdere berekeningen.
4.4.6.3 Alternatieve oplossing voor integraal 1
Volgens de bekende integraalformules geldt:
\[ \int \frac{dx}{x \sqrt{a x^{2} + b x + c}} = \frac{1}{\sqrt{-c}} \arcsin \left( \frac{b x + 2c}{\sqrt{b^{2} - 4ac}} \right)+C, \qquad (c < 0) \]Dus:
\[ \phi_A - \phi_P =\int_P^A \frac{1}{r\sqrt{(A - r)(r - P)}} \, dr = \int_P^A \frac{1}{r\sqrt{(-r^2+(A+P)r-AP}} \, dr \] \[ \frac{1}{\sqrt{AP}}\arcsin\left[\frac{(A+P)r-2AP}{|r|\sqrt{(A+P)^2-4AP}}\right]_p^A \] \[ \frac{1}{\sqrt{AP}} \left[ \arcsin\frac{(A+P)A-2AP}{|A|\sqrt{(A+P)^2-4AP}} - \arcsin\frac{(A+P)P-2AP}{|P|\sqrt{(A+P)^2-4AP}} \right] \] \[ \frac{1}{\sqrt{AP}} \left[ \arcsin\frac{(A-P)A}{|A|(A-P)} - \arcsin\frac{(P-A)P}{|P|(A-P)} \right] \] \[ \frac{1}{\sqrt{AP}} \left[ \arcsin(1) - \arcsin(-1) \right] \] \[ \frac{1}{\sqrt{AP}} \left[ \frac{\pi}{2} - \left( \frac{-\pi}{2} \right) \right] =\frac{\pi}{\sqrt{AP}} \]Dus:
\[ \phi_{A} - \phi_{P} = =\frac{\pi}{\sqrt{AP}} \]4.4.6.4 Gedetailleerde berekening van de omlooptijd
Uit:
\[ L = r^{2} \frac{d\phi}{d\tau} \quad \Rightarrow \quad d\tau = \frac{r^{2}}{L} d\phi \]volgt voor de periode:
\[ T = \int d\tau = \int_{0}^{2\pi} \frac{r^{2}}{L} d\phi \]Gebruikmakend van vergelijking (40):
\[ d\phi = \sqrt{\frac{L^{2}/c^2}{1-E^2/c^4}} \left[ \frac{1}{r\sqrt{(A - r)(r - P)}} + \frac{\varepsilon/2}{r^2\sqrt{(A - r)(r - P)}} \right] dr \tag{40} \] \[ d\tau = \frac{r^2}{L} \sqrt{\frac{L^{2}/c^2}{1-E^2/c^4}} \left[ \frac{1}{r\sqrt{(A - r)(r - P)}} + \frac{\varepsilon/2}{r^2\sqrt{(A - r)(r - P)}} \right] dr \] \[ d\tau = \frac{1}{L} \sqrt{\frac{L^{2}/c^2}{1-E^2/c^4}} \left[ \frac{r}{\sqrt{(A - r)(r - P)}} + \frac{\varepsilon/2}{\sqrt{(A - r)(r - P)}} \right] dr \] \[ \Delta T =\int d\tau = \frac{2}{L} \sqrt{\frac{L^{2}/c^2}{1-E^2/c^4}} \int_P^A \left[ \frac{r}{\sqrt{(A - r)(r - P)}} + \frac{\varepsilon/2}{\sqrt{(A - r)(r - P)}} \right] dr \]Eerst de uitwerking van de linkerintegraal:
\[ \int_P^A \frac{r}{\sqrt{(A - r)(r - P)}}dr = \int_P^A \frac{r}{\sqrt{-r^2+(A+P)r-AP}} dr \tag{41} \]Volgens de lijst van integralen (Wikipedia): (https://nl.wikipedia.org/wiki/Lijst_van_integralen)
\[ \int \frac{x}{\sqrt{ax^2+bx+c}}dx=\frac{\sqrt{ax^2+bx+c}}{a}- \frac{b}{2a}\int \frac{1}{\sqrt{ax^2+bx+c}}dx \tag{42} \]En:)
\[ \int \frac{1}{\sqrt{ax^2+bx+c}}dx=\frac{1}{\sqrt{-a}}\arcsin\frac{-2ax-b}{\sqrt{b^2-4ac}}+C, \quad (a<0) \]Om de linkerintegraal om te zetten naar de integraalformule:
\[ \int_P^A \frac{r}{\sqrt{-r^{2} + (A + P)r-AP}} \, dr= \] \[ =\left[ \frac{\sqrt{-r^2+(A+P)r-AP}}{-1}\right]_P^A -\frac{A+P}{-2} \int_P^A \frac{1}{\sqrt{-r^{2} + (A + P)r-AP}} \, dr= \] \[ =-\sqrt{A^{2} + (A + P)A-AP}+\sqrt{-P^2+(A+P)P-AP}+\frac{A+P}{2} \int_P^A \frac{1}{\sqrt{-r^{2} + (A + P)r-AP}} \, dr= \] \[ =-0+0+ \frac{A+P}{-2} \int_P^A \frac{1}{\sqrt{-r^{2} + (A + P)r-AP}} \, dr \]Nu alleen de integraal:
\[ \int_P^A \frac{1}{\sqrt{-r^{2} + (A + P)r-AP}} \, dr =\left[\arcsin \frac{2r-(A+P)}{\sqrt{(A+P)^2-4AP}}+C \right]_P^A= \] \[ =\arcsin \frac{2A-(A+P)}{\sqrt{(A+P)^2-4AP}}+C-\arcsin \frac{2P-(A+P)}{\sqrt{(A+P)^2-4AP}}+C= \] \[ =arcsin \frac{A-P}{A-P}-\arcsin \frac{-A+P}{A-P} \] \[ \frac {\pi}{2}+\frac{\pi}{2}=\pi \]Dus, de linkerintegraal levert:
\[ \frac{(A+P)\pi}{2} \]De rechterintegraal levert:
\[ \pi\frac{\varepsilon}{2} \]De som is:
\[ \frac{\pi}{2}(A+P+\varepsilon) \]Dus, de totale integraal voor een volledige omwenteling is:
\[ \Delta T = \frac{2}{L} \sqrt{\frac{L^{2}/c^{2}}{1 - E^{2}/c^{4}}} \frac{\pi}{2}(A+P+\varepsilon) \]Met:
\[ \varepsilon = \frac{R_{s}}{1 - R_{s}/D} \] \[ \Delta T = \frac{2}{L} \sqrt{\frac{L^{2}/c^{2}}{1 - E^{2}/c^{4}}} \frac{\pi}{2} \left( A+P + \frac{R_{s}}{1 - R_{s}/D} \right) \] \[ \Delta T = 2\pi \frac{A+P}{2L} \sqrt{\frac{L^{2}/c^{2}}{1 - E^{2}/c^{4}}} \left( 1 + \frac{R_{s}}{(A+P)(1 - \frac{R_s}{D})} \right) \] \[ \Delta T = 2\pi \frac{A+P}{2L} \sqrt{\frac{AP}{1 - R_s/D}} \left( 1 + \frac{R_{s}}{(A+P)(1 - \frac{R_s}{D})} \right) \]Voor Mercurius:
- \(A = 6.98 \times 10^{10}\,\mathrm{m}\)
- \(P = 4.60 \times 10^{10}\,\mathrm{m}\)
- \(D = 2.77 \times 10^{10}\,\mathrm{m}\)
- \(R_{s(sun)} = 2953.25\,\mathrm{m}\)
De tijd voor één omwenteling is:
\[ \Delta T = 7598744\,\mathrm{s} \Rightarrow \frac{7598744}{24*3600}= 87.95\,\text{dagen} \]Afgeleid in hoofdstuk Schwarzschild-Benadering 4.8.2., vergelijking 𝟐𝒅, de instantane rotatiesnelheid van Mercurius als functie van \(\phi\):
\[ v=\left[\frac{GM_{sun}}{a(1-e^2)}(1+2e\cos[\phi(1-\epsilon)]+e^2)\right]^2 \tag{42a} \]4.4.7 Fysische betekenis
- Waarom precessie: Door de kromming van ruimte-tijd rond de zon is de baan van Mercurius geen perfecte ellips, maar een ellips die langzaam roteert.
- Geen Newtonse verklaring: Dit effect kan niet worden verklaard door klassieke mechanica of planetaire verstoringen alleen.
- Empirische bevestiging: De gemeten waarde van circa 43 boogseconden per eeuw was één van de eerste grote successen van de algemene relativiteitstheorie.
4.4.8 Kerninzicht
- De precessie van Mercurius’ perihelium is een direct en meetbaar gevolg van de kromming van ruimte-tijd zoals voorspeld door de Schwarzschild-metriek.
- De kwantitatieve overeenstemming tussen theorie en waarneming vormt een van de krachtigste bevestigingen van Einsteins algemene relativiteitstheorie.
4.5 Experiment 5 – Shapiro-Tijdvertraging
Inleiding en Fysisch Idee
De Shapiro-tijdvertraging is het effect waarbij een lichtsignaal (of radargolf) dat langs een massief object (zoals de zon) reist, langer onderweg is dan verwacht op basis van een rechte lijn in vlakke ruimte-tijd. Dit is een direct gevolg van de kromming van de ruimte-tijd door massa, zoals voorspeld door de algemene relativiteitstheorie.
Historie:
Het effect werd in 1964 voorspeld door Irwin Shapiro en sindsdien in vele experimenten
bevestigd, onder andere door radarsignalen naar Venus en Mercurius te sturen en
de retourtijd te meten.
In het Shapiro-experiment werden radarsignalen vanaf de aarde naar een planeet gestuurd, die op dat moment aan de andere kant van de zon stond. Deze signalen weerkaatsten terug naar de aarde. Volgens de algemene relativiteitstheorie zal het signaal, dat net langs de zon scheert, worden afgebogen door de zwaartekracht van de zon, of eigenlijk vervormt de massa van de zon de ruimte-tijd zodanig dat het signaal een “rechte gekromde” lijn volgt.
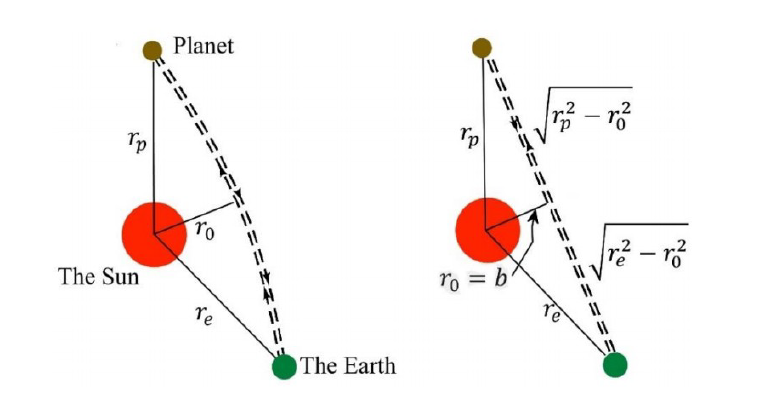
(Uit Tests of General Relativity: A Review door Estelle Asmodelle (Asmodelle, 2017))
Voor de berekening van de Shapiro-vertraging wordt de Schwarzschild-vergelijking toegepast:
\[
ds^{2}
=
c^{2} d\tau^{2}
=
\sigma^{2} c^{2} dt^{2}
-
\frac{dr^{2}}{\sigma^{2}}
-
r^{2} d\theta^{2}
-
r^{2}\sin^{2}\theta \, d\phi^{2}
\]
Waarbij:
en
4.5.1 Afleiding op basis van de Schwarzschild-metriek
We kiezen het referentiekader zodanig dat het overeenkomt met het equatoriale vlak, (\( \theta = \pi/2 \) )
Dan geldt:
\[ c^2 d\tau^2 = \sigma^2 c^2 dt^2 - \frac{dr^2}{\sigma^2} - r^2 d\phi^2 \]Voor fotonen of radar echo’s geldt \(d\tau = 0\), dus: \[ \sigma^2 c^2 dt^2 = \frac{dr^2}{\sigma^2} + r^2 d\phi^2 \]
Afleiding naar de affiene parameter \(\lambda\): \[ \sigma^2 c^2 \left(\frac{dt}{d\lambda}\right)^2 = \frac{1}{\sigma^2} \left(\frac{dr}{d\lambda}\right)^2 + r^2 \left(\frac{d\phi}{d\lambda}\right)^2 \]
Zoals afgeleid in formule 11 uit hoofdstuk 4.2 is het impulsmoment: \[ L = r^2 \frac{d\phi}{d\lambda} \] en \[\sigma^2 c^2 \left(\frac{dt}{d\lambda}\right)^2 = \frac{1}{\sigma^2} \left(\frac{dr}{d\lambda}\right)^2 + \frac{L^2}{r^2} \]
Vermenigvuldig met \(\sigma^2\): \[ \sigma^4 c^2 \left(\frac{dt}{d\lambda}\right)^2 = \left(\frac{dr}{d\lambda}\right)^2 + \frac{L^2}{r^2} \sigma^2 \]
Stel:
\[
k^2 = \sigma^4 \left(\frac{dt}{d\lambda}\right)^2
\]
Opmerking: Dit is ook \(k = E /c^2\) zoals te zien in formule 9a uit hoofdstuk 4.2.
Dan is:
\[\left(\frac{dr}{d\lambda}\right)^2 + \frac{L^2}{r^2} \sigma^2 = k^2 c^2\] De energievergelijking voor een fotonenbaan in de Schwarzschild-geometrie is dus: \[ \left(\frac{dr}{d\lambda}\right)^2 + \frac{L^2}{r^2} \left(1 - \frac{R_s}{r}\right) = k^2 c^2 \tag{42b} \]
Zoals eerder is afgeleid: \[ k^2 = \sigma^4 \left(\frac{dt}{d\lambda}\right)^2 \Rightarrow \left(\frac{dt}{d\lambda}\right)^2 = \frac{k^2}{\sigma^4} \]
Waarbij we gebruiken: \[ \left(\frac{dt}{d\lambda}\right)^2 = \frac{k^2}{\sigma^4} = \frac{k^2}{(1-R_s/r)^2} \]
Nu is: \[ \left(\frac{dr}{d\lambda}\right)^2 = \left(\frac{dr}{dt} \frac{dt}{d\lambda}\right)^2 = \frac{k^2}{(1-R_s/r)^2} \left(\frac{dr}{dt}\right)^2 \tag{42c} \]
We kunnen de energievergelijking (42b) herschrijven: \[ \left(\frac{dr}{d\lambda}\right)^2 +\frac{L^2}{r^2}\left(1-\frac{R_s}{r}\right)=k^2c^2 \] Vervang \(\left(\frac{dr}{d\lambda}\right)^2 \) door (42c): \[ \frac{k^2}{(1-R_s/r)^2} \left(\frac{dr}{dt}\right)^2 + \frac{L^2}{r^2} (1-R_s/r) = k^2 c^2 \] Deel door \((1-R_s/r)\): \[ \frac{k^2}{(1-R_s/r)^3} \left(\frac{dr}{dt}\right)^2 + \frac{L^2}{r^2} - \frac{k^2 c^2}{1-R_s/r} = 0 \]
Vervolgens delen we door \(k^2\): \[ \frac{1}{(1-R_s/r)^3} \left(\frac{dr}{dt}\right)^2 + \frac{L^2}{k^2r^2} - \frac{c^2}{1-R_s/r} = 0 \tag{43} \] Beschouw nu het pad van een foton van de Aarde naar een andere planeet (bijvoorbeeld Venus, met \(r_p=r_v\)), zoals weergegeven in Figuur 2. Het is duidelijk dat het pad van het foton zal worden afgebogen door het zwaartekrachtsveld van de Zon. Laat \(r_0\) de coördinatenafstand zijn van het dichtste punt waar het foton de Zon nadert; dan geldt: \[ \left(\frac{dr}{dt}\right)_{r_0}=0 \] Dan vinden we uit (43) de relatie tussen de constanten: \[ \frac{L^2}{k^2r^2} = \frac{c^2}{1-R_s/r} \] Na herschikking kunnen we (43) schrijven als: \[ \left(\frac{dr}{dt}\right)^2 =\left(1-R_s/r\right)^3\left(-\frac{L^2}{k^2r^2} + \frac{c^2}{1-R_s/r}\right) =\left(1-R_s/r\right)^3\left(\frac{c^2}{1-R_s/r}-\frac{L^2r_0^2}{k^2r_0^2r^2}\right) \] \[ =\left(1-R_s/r\right)^2\left(c^2-\frac{r_0^2c^2(1-R_s/r)}{r^2(1-R_s/r_0)}\right) =c^2\left(1-R_s/r\right)^2\left(1-\frac{r_0^2(1-R_s/r)}{r^2(1-R_s/r_0)}\right) \] \[ \Rightarrow \frac{dr}{dt}=c\left(1-R_s/r\right)\left[1-\frac{r_0^2(1-R_s/r)}{r^2(1-R_s/r_0)}\right]^{1/2} \]
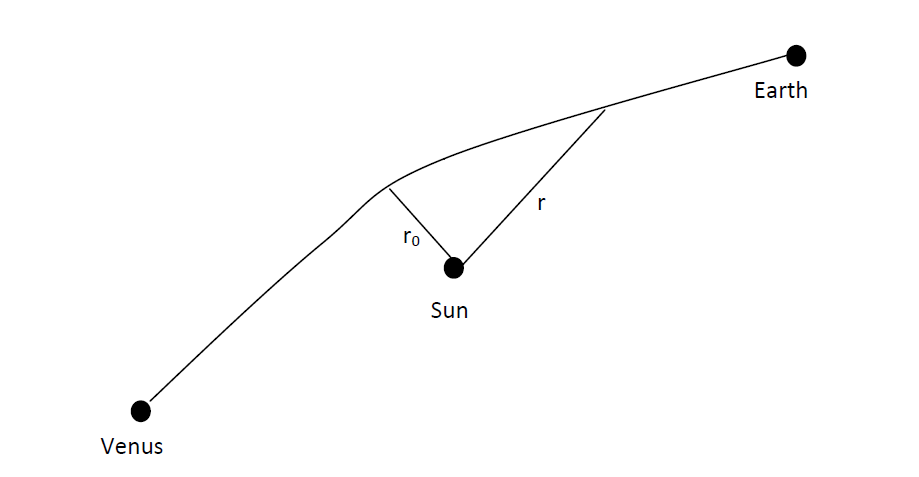
Dit kan worden geïntegreerd om de tijd te bepalen die nodig is om te reizen tussen punt \(r_0\) en \(r\): \[ t(r,r_0)=\int_{r_0}^{r} \frac{1}{c\left(1-R_s/r\right)\left[1-\frac{r_0^2(1-R_s/r)}{r^2(1-R_s/r_0)} \right]^{1/2}}\,dr \]
4.5.1.1 Eerste‑orde benadering
Omdat \(R_{s} \ll r_{0}\), kunnen we de eerste‑orde Taylor‑benadering nemen van:
\[ \frac{1 - \frac{R_{s}}{r}}{1 - \frac{R_{s}}{r_{0}}} \approx \left(1 - \frac{R_{s}}{r}\right) \left(1 + \frac{R_{s}}{r_{0}}\right) = 1 - \frac{R_{s}}{r} + \frac{R_{s}}{r_{0}} - \frac{R_{s}^{2}}{rr_{0}} \]Dus kan de integrand worden uitgebreid tot de eerste orde in \(R_{s}/r\):
\[ t(r,r_{0}) =\int_{r_0}^r \frac{1}{c(1-R_s/r)\left[1-\frac{r_0^2}{r^2} \left(1-\frac{R_s}{r}+\frac{R_s}{r_0}-\frac{R_s^2}{rr_0}\right)\right]^{1/2}}\, dr \]Vermenigvuldig de teller en de noemer met \(r\):
\[ t(r,r_{0}) =\int_{r_0}^r \frac{r}{c(1-R_s/r)\left[r^2-r_0^2 \left(1-\frac{R_s}{r}+\frac{R_s}{r_0}-\frac{R_s^2}{rr_0}\right)\right]^{1/2}}\, dr \] \[ t(r,r_{0}) =\int_{r_0}^r \frac{r}{c(1-R_s/r)\left[r^2-r_0^2-R_sr_0 +\frac{R_sr_0^2}{r}+\frac{R_s^2r_0}{r}\right]^{1/2}}\, dr \] \[ t(r,r_{0}) =\int_{r_0}^r \frac{r}{c\sqrt{r^2-r_0^2}(1-R_s/r)\left[1- \frac{R_sr_0\left(1-\frac{r_0}{r}-\frac{R_s}{r}\right)}{r^2-r_0^2}\right]^{1/2}}\, dr \] \[ t(r,r_{0}) =\int_{r_0}^r \frac{r}{c\sqrt{r^2-r_0^2}\left[\left(1-\frac{2R_s}{r}+\frac{R_s^2}{r^2}\right)\left(1- \frac{R_sr_0\left(1-\frac{r_0}{r}-\frac{R_s}{r}\right)}{r^2-r_0^2}\right)\right]^{1/2}}\, dr \]Eerst werken we de rechterkant van de teller uit:
\[ \left(1-\frac{2R_s}{r}+\frac{R_s^2}{r^2}\right)\left(1- \frac{R_sr_0\left(1-\frac{r_0}{r}-\frac{R_s}{r}\right)}{r^2-r_0^2}\right) \] \[ 1-\frac{2R_s}{r}+\frac{R_s^2}{r^2}-\frac{R_sr_0\left(1-\frac{r_0}{r}-\frac{R_s}{r}\right)}{r^2-r_0^2} +\frac{2R_s^2r_0\left(1-\frac{r_0}{r}-\frac{R_s}{r}\right)}{r(r^2-r_0^2)} -\frac{R_s^3r_0\left(1-\frac{r_0}{r}-\frac{R_s}{r}\right)}{r^2(r^2-r_0^2)} \]Na het negeren van de kleinste termen:
\[ \left(1-\frac{2R_s}{r}+\frac{R_s^2}{r^2}\right)\left(1- \frac{R_sr_0\left(1-\frac{r_0}{r}-\frac{R_s}{r}\right)}{r^2-r_0^2}\right) \approx 1-\frac{2R_s}{r}-\frac{R_sr_0\left(1-\frac{r_0}{r}\right)}{r^2-r_0^2} \] \[ \left(1-\frac{2R_s}{r}+\frac{R_s^2}{r^2}\right)\left(1- \frac{R_sr_0\left(1-\frac{r_0}{r}-\frac{R_s}{r}\right)}{r^2-r_0^2}\right) \approx 1-\frac{2R_s}{r}-\frac{R_sr_0\left(r-r_0\right)}{r(r+r_0)(r-r_0)} \] \[ \left(1-\frac{2R_s}{r}+\frac{R_s^2}{r^2}\right)\left(1- \frac{R_sr_0\left(1-\frac{r_0}{r}-\frac{R_s}{r}\right)}{r^2-r_0^2}\right) \approx 1-\frac{2R_s}{r}-\frac{R_sr_0}{r(r+r_0)} \]Vul de noemer in:
\[ t(r,r_{0}) =\int_{r_0}^r \frac{r}{c\sqrt{r^2-r_0^2}\left[1-\frac{2R_s}{r}-\frac{R_sr_0}{r(r+r_0)}\right]^{1/2}}\, dr \]Bij wederom een Taylor‑benadering van de eerste orde verkrijgen we:
\[ t(r,r_{0}) =\int_{r_0}^r \frac{r}{c\sqrt{r^2-r_0^2}}\left[1+\frac{R_s}{r}+\frac{R_sr_0}{2r(r+r_0)}\right]\, dr \]Dit kan worden herleid tot (zie controle hieronder):
\[ t(r,r_{0}) = \frac{\sqrt{r^{2}-r_{0}^{2}}}{c} + \frac{R_{s}}{c} \ln\!\left(\frac{ r + \sqrt{r^{2}-r_{0}^{2}}}{r_0} \right) + \frac{R_{s}}{2c} \left(\frac{r - r_{0}}{r + r_{0}}\right)^{1/2} \]Controleren van bovenstaande formule
We kunnen de bovenstaande formule controleren door de afgeleide te nemen; die moet gelijk zijn aan de integrand:
\[ \frac{dt(r,r_0)}{dr}=\frac{r}{c(r^2-r_0^2)^{1/2}}+ \frac{R_s}{c} \frac{\left( \frac{1}{r_0}+\frac{r}{r_0(r^2-r_0^2)^{1/2}}\right)}{\frac{r+(r^2-r_0^2){1/2}}{r_0}} +\frac{R_s}{4c}\frac{\left(\frac{1}{r+r_0}-\frac{r-r_0}{(r+r_0)^{2}} \right)}{\left( \frac{r-r_0}{r+r_0}\right)^{1/2}} \] \[ \frac{dt(r,r_0)}{dr}=\frac{r}{c(r^2-r_0^2)^{1/2}}+ \frac{R_s}{c} \frac{\left( 1+\frac{r}{(r^2-r_0^2)^{1/2}}\right)}{r+(r^2-r_0^2){1/2}} +\frac{R_s}{4c}\frac{\left(\frac{r+r_0-r+r_0}{(r+r_0)^{2}} \right)} {\left( \frac{r-r_0}{r+r_0}\right)^{1/2}} \] \[ \frac{dt(r,r_0)}{dr}=\frac{r}{c(r^2-r_0^2)^{1/2}}+ \frac{R_s}{c} \frac{\left[ r+(r^2-r_0^2)^{1/2}\right]}{\left[r+(r^2-r_0^2)^{1/2}\right](r^2-r_0^2)^{1/2}} +\frac{R_s}{4c} \frac{\left(r+r_0-r+r_0\right)} {\left( \frac{r-r_0}{r+r_0}\right)^{1/2}(r+r_0)^{2}} \] \[ \frac{dt(r,r_0)}{dr}=\frac{r}{c(r^2-r_0^2)^{1/2}}+ \frac{R_s}{c} \frac{1}{(r^2-r_0^2)^{1/2}} +\frac{R_s}{2c} \frac{r_0} {\left( \frac{r-r_0}{r+r_0}\right)^{1/2}(r+r_0)^{2}} \] \[ \frac{dt(r,r_0)}{dr}=\frac{r}{c(r^2-r_0^2)^{1/2}}+ \frac{R_s}{c} \frac{1}{(r^2-r_0^2)^{1/2}} +\frac{R_s}{2c} \frac{r_0} {(r-r_0)^{1/2}(r+r_0)} \] \[ \frac{dt(r,r_0)}{dr}=\frac{r}{c(r^2-r_0^2)^{1/2}} \left[ 1+ \frac{R_s}{r}+\frac{R_sr_0}{2r(r+r_0)} \right] \]Dus de formule is correct!
Dus:
\[ t(r,r_{0}) = \frac{\sqrt{r^{2}-r_{0}^{2}}}{c} + \frac{R_{s}}{c} \ln\!\left(\frac{ r + \sqrt{r^{2}-r_{0}^{2}}}{r_0} \right) + \frac{R_{s}}{2c} \left(\frac{r - r_{0}}{r + r_{0}}\right)^{1/2} \]De eerste term aan de rechterkant is precies wat we zouden verwachten als het licht in een rechte lijn zou reizen. De tweede en derde termen geven de extra coördinatietijd die nodig is voor het foton om langs het gekromde pad naar het punt \(r\) te reizen.
Zoals te zien in Figuur 2, als we een radarstraal naar Venus sturen en terug, dan is de extra coördinatietijd ten opzichte van een rechte lijn:
\[ \Delta t = 2\left[ t(r_{E},r_{0}) + t(r_{V},r_{0}) - \frac{\sqrt{r_{E}^{2}-r_{0}^{2}}}{c} - \frac{\sqrt{r_{V}^{2}-r_{0}^{2}}}{c} \right] \]Zoals eerder vermeld, vormen de eerste twee termen binnen deze haakjes de relativistische tijd van de Aarde naar Venus, en de twee termen aan de rechterkant vormen de tijd als het pad gewoon een rechte lijn zou zijn. De factor 2 is inbegrepen omdat het foton naar Venus moet gaan en terug naar de Aarde.
Aangezien \(r_{E} \gg r_{0}\) en \(r_{V} \gg r_{0}\) hebben we:
\[ t(r_{E},r_{0}) - \frac{\sqrt{r_{E}^{2}-r_{0}^{2}}}{c} \approx \frac{R_{s}}{c} \ln\!\left( \frac{r_{E} + r_{E}}{r_{0}} \right) + \frac{R_{s}}{2c} = \frac{R_{s}}{c} \ln\!\left( \frac{2r_{E}}{r_{0}} \right) + \frac{R_{s}}{2c} \] \[ t(r_{V},r_{0}) - \frac{\sqrt{r_{V}^{2}-r_{0}^{2}}}{c} \approx \frac{R_{s}}{c} \ln\!\left( \frac{r_{V} + r_{V}}{r_{0}} \right) + \frac{R_{s}}{2c} = \frac{R_{s}}{c} \ln\!\left( \frac{2r_{V}}{r_{0}} \right) + \frac{R_{s}}{2c} \]Sommatie:
\[ \frac{R_{s}}{c} \ln\!\left(\frac{2r_{E}}{r_{0}}\right) + \frac{R_{s}}{c} \ln\!\left(\frac{2r_{V}}{r_{0}}\right) + \frac{R_{s}}{c} = \frac{2GM}{c^{3}} \left[ \ln\!\left( \frac{4 r_{E} r_{V}}{r_{0}^{2}} \right) + 1 \right] \]Dus om naar Venus en terug te gaan, is de extra coördinaattijdvertraging:
\[ \Delta t \approx \frac{4GM_{\text{sun}}}{c^{3}} \left[ \ln\!\left( \frac{4 r_{E} r_{V}}{r_{0}^{2}} \right) + 1 \right] \]Hieruit blijkt ook dat de tijdvertraging groter wordt naarmate de impactparameter \(r_{0}\) (de afstand tot het zwaartekrachtscentrum) kleiner wordt.
Numerieke Waarden
- Voor Venus, tegenover de Aarde aan de andere kant van de Zon: \(\Delta t ≈ 252\, μs\)
- Voor Mercurius geldt: \(\Delta t ≈ 240\, μs\)
- Afstand Venus-Zon \(r_V : 108 × 10^9 \,m\)
- Afstand Zon-Aarde \(r_E : 150 × 10^9 \,m\)
- Totaal afstand Venus-Aarde: \(258 × 10^9 \,m\)
- Totale reistijd (Aarde → Zon → Venus → Aarde) zonder vertraging: \(1720\, s\)
De Shapiro‑vertraging is dus klein, maar een duidelijk meetbaar effect.
4.5.1.2 Eigentijd van Aarde versus coördinaattijd
Klokken op Aarde meten geen coördinaattijd, vanwege de rotatie van de Aarde om haar eigen
as en het effect van de rotatie van de Aarde rond de Zon.
Door de rotatie van de Aarde om haar eigen as wordt de overeenkomstige eigen tijd van het signaal
gegeven door:
\[\Delta \tau = \sqrt{1 - \frac{2 G M_E}{c^2 r_E}} \, \Delta t\]
Het effect is dus: \[ \Delta t -\Delta \tau =\Delta t \sqrt{1 - \frac{2 G M_E}{c^2 r_E}} \, \Delta t \] Dt geeft: \[ \Rightarrow 6.98*10^{-10} \Delta t \,\, voor \,\, 252 \, \mu s \Rightarrow 1.76* 10^{-13} seconden=0.176\,ps \] \[ p=10^{-12} \]
Aangezien \(r_E\,\gg\, GM/c^2\), en dus \(0.176\,ps \,\ll \,252\, \mu s\)
is dit effect verwaarloosbaar.
Het effect van de rotatie van de Aarde rond de Zon veroorzaakt een vertraging van
15 nanoseconden per seconde, zoals vermeld in hoofdstuk (4.6).
Voor de extra tijdvertraging \( \Delta t \approx 252\, \mu s\) vanaf Venus, veroorzaakt de rotatie van de
Aarde rond de Zon een klein effect van: \(252∗10^{−6}∗15∗10^{-9}=3.78∗10^{−12}\, 𝑠𝑒𝑐𝑜𝑛𝑑𝑒𝑛=3.78\, 𝑝𝑠\), wat
ook genegeerd kan worden.
4.5.2 Fysische Interpretatie
- De extra tijdsvertraging is een direct gevolg van de kromming van ruimte-tijd door de zon.
- Het effect is het grootst als het signaal dicht langs de zon gaat (kleine r0).
- Experimenten tonen aan dat de gemeten tijdsvertraging exact overeenkomt met de voorspellingen van de algemene relativiteitstheorie.
4.5.3 Praktisch belang
- Belangrijk voor nauwkeurige navigatie van ruimtemissies en het testen van alternatieve zwaartekrachtstheorieën.
- Wordt gebruikt in pulsar-timing en bij het interpreteren van signalen van ruimtevaartuigen.
4.5.4 Kerninzicht
De Shapiro-tijdvertraging is een van de vier klassieke experimenten die de algemene relativiteitstheorie bevestigen. Het effect is klein, maar meetbaar en volledig verklaarbaar met de Schwarzschild-metriek.
4.6 Tijdsrelatie tussen Waarnemer op Aarde en het Centrum van de Zon
Wanneer we de afbuiging van licht of de banen van planeten rond de Zon beschouwen, dan wordt een referentiekader gebruikt met het centrum in het midden van de Zon, terwijl wij het fenomeen vanaf de Aarde observeren en een rotatiesnelheid hebben ten opzichte van de Zon. In dit hoofdstuk onderzoeken we de tijdsrelatie tussen een waarnemer op de Aarde en het centrum van de Zon, met de bijbehorende correctiefactoren.
Het vertrekpunt is de Schwarzschild-metriek, die de ruimte-tijd rondom een sferisch symmetrisch massief object beschrijft. De metriek wordt gegeven door:
\[ ds^2 = \sigma^2 c^2 dt^2 - \frac{dr^2}{\sigma^2} - r^2 d\theta^2 - r^2 \sin^2\theta \, d\phi^2 \]waarbij:
\[ \sigma =\sqrt{ 1 - \frac{2 G M_{\text{sun}}}{c^2 r}}, \qquad R_s = \frac{2 G M_{\text{sun}}}{c^2} \]- G is de gravitatieconstante,
- Msun is de massa van de Zon,
- c is de lichtsnelheid,
- R is de afstand tot het centrum van de Zon.
De coördinaten \(\theta\) en \(\phi\) representeren de gebruikelijke bolvormige coördinaten. We beperken ons tot het equatorvlak van de Zon, zodat \(\theta\, =\, \pi /2\) en de straal \(r\) constant is.
4.6.1 Vergemakkelijking van de Schwarzschild-metriek
Voor een waarnemer op de Aarde nemen we aan dat de Aarde zich in een cirkelvormige baan rond de Zon bevindt. De tijdsmeting van de waarnemer op Aarde wordt beschreven door de eigen tijd dτ, terwijl dt de coördinaattijd is in het Zon-referentiekader.
De Schwarzschild-metriek reduceert dan tot:
\[ ds^2 = c^2 d\tau^2 = \sigma^2 c^2 dt^2 - r^2 d\phi^2 \]Dit kan herschreven worden als:
\[ d\tau^2 = \sigma^2 dt^2 - \frac{r^2}{c^2} \left( \frac{d\phi}{dt} \right)^2 dt^2 \]Invullen van \(\sigma\) levert:
\[ d\tau^2 = \left( 1 - \frac{R_s}{r} - \frac{r^2}{c^2} \left( \frac{d\phi}{dt} \right)^2 \right) dt^2 \]4.6.2 Tijdsvertraging door Zwaartekracht en Beweging van de Aarde
Voor een waarnemer op Aarde geldt:
\[ d\tau^2 = \left( 1 - \frac{R_s}{r} - \frac{v^2}{c^2} \right) dt^2 \] \[ d\tau = \sqrt{ 1 - \frac{R_s}{r} - \frac{v^2}{c^2} } \, dt \]waarbij \(R_s\) de Schwarzschildstraal van de Zon is, v de snelheid van de Aarde in haar baan, en \(r\) de afstand van de Aarde tot het centrum van de Zon. Dit is de algemene tijdsrelatie die rekening houdt met zowel de zwaartekracht van de Zon als de snelheid van de Aarde.
Numerieke waarden:
- \( R_s = 2950 \,\text{m} \)
- \( v =30.000 \,\text{m/s} \)
- \( r = 150 \times 10^{9} \,\text{m (de gemiddelde afstand van de Aarde tot de Zon).} \)
Door de waarden in te vullen en de uitdrukking voor \(d\tau\) uit te breiden met een Taylorreeks tot de eerste orde, krijgen we de volgende benadering:
\[ d\tau \approx \left( 1 - \frac{R_s}{2r} - \frac{v^2}{2c^2} \right) dt \]
De tweede term aan de rechterkant is het gevolg van de zwaartekracht van de Zon en de derde term
is het gevolg van de snelheid van de Aarde rond de Zon.
Substitutie van de numerieke waarden levert:
Dit betekent een tijdsvertraging van ongeveer 15 nanoseconden per seconde voor een waarnemer op Aarde ten opzichte van de Zon-coördinaattijd.
4.6.3 Correctiefactor voor de Zwaartekracht van de Aarde
De zwaartekracht van de Aarde zelf levert eveneens een bijdrage:
\[ d\tau = \sqrt{ 1 - \frac{2 G M_E}{c^2 r_E} } \, dt \]Met:
- \( M_E = 5.9742 \times 10^{24} \,\text{kg}\,\text{(massa van de aarde)} \)
- \( r_E = 6.381 \times 10^{6} \,\text{m}\, \text{(straal van de aarde)}\)
Dit geeft: \[ d\tau=\sqrt{1-1.3908*10^{-9}}dt \approx \left( 1 - 0.6954 \times 10^{-9} \right) dt \]
Voor een waarnemer op de evenaar is de rotatiesnelheid \(v_{rot}\) van de Aarde ook van belang. De hoeksnelheid \(d\phi/dt\) van de Aarde wordt gegeven door de rotatieperiode van de Aarde (siderische periode: \(86162.4 \text{ seconden}\)):
\[ \frac{d\phi}{dt} = \frac{2\pi}{T_{tot}} = \frac{2\pi}{86162.4} = 7.2923 \times 10^{-5} \,\text{rad/s} \]De aangepaste tijdsrelatie voor een waarnemer op de evenaar, inclusief de rotatie van de Aarde, wordt dan:
\[ d\tau=\sqrt{\left(1-\frac{R_E}{r^e}-\frac{v_E^2}{c^2}\right)}\,dt \]waarbij de tweede term de bijdrage van de rotatiesnelheid van de Aarde betreft. Door de juiste waarden in te vullen, krijgen we de uiteindelijke tijdsrelatie:
\[ d\tau = \sqrt{ 1 - 1.3908 \times 10^{-9} - 2.4059 \times 10^{-12}} dt \] \[ d\tau \approx \left( 1 - 0.6966 \times 10^{-9} \right) dt \]Waarbij:
- \( R_E = 0.008875 \,\text{m} \) (Schwarzschild-radius van de Aarde)
- \( r_e = 6{,}381{,}000 \,\text{m} \) (straal van de Aarde)
- \( v_E = 465 \,\text{m/s} \) (rotatie van de Aarde om haar as)
- \( c = 3 \cdot 10^{8} \,\text{m/s} \)
4.6.4 Conclusie
De tijdsrelatie tussen een waarnemer op Aarde en het centrum van de Zon wordt bepaald door drie effecten: de zwaartekracht van de Zon, de baansnelheid van de Aarde en de lokale zwaartekracht van de Aarde zelf. Samen veroorzaken zij een kleine maar meetbare tijdsvertraging.
4.6.5 Fysische Betekenis
- Klokken op Aarde lopen langzamer dan een hypothetische klok in het Zon-centrum.
- Deze correcties zijn essentieel voor GPS, ruimtevaart en precisietiming.
4.7 Alternatieve Afleiding van de Baanvergelijking
Volgens de eerste wet van Kepler zijn alle planeetbanen om de zon ellipsvormig. Zoals we in hoofdstuk 4.4 hebben gezien heeft de Algemene Relativiteitstheorie aangetoond dat er ook een relativistische correctie is op de ellipsvorm die de periheliumprecessie van bijvoorbeeld Mercurius verklaart.
We geven daarom hier een alternatieve afleiding van de baanvergelijking voor een massief deeltje in de Schwarzschild-geometrie die een oplossing geeft die ons dichter bij de oorspronkelijke formule van een ellips brengt.
Deze is: \[ r(\phi) = a\,\frac{1 - e^{2}}{1 + e \cos(\phi - \theta)} \]
Deze vergelijking wordt vergeleken met de relativistische uitkomst (zie vergelijking 3.5.5a) aan het einde van dit hoofdstuk: \[ r = a\,\frac{1 - e^{2}}{1 + e \cos(\phi - \epsilon \phi)} \]
Hier zien we dat \( \theta \) niet een constante is maar een functie van \( \phi \) en verandert met een factor \( \epsilon \).
Uit General Relativity: An Introduction for Physics door M. P. Hobson, G. Efstathiou en A. N. Lasenby, pag. 230 (Hobson, 2006).
We beperken ons tot het equatorvlak \( \theta = \pi/2 \), zodat de Schwarzschild-metriek voor een massief deeltje reduceert tot: \[ c^{2} d\tau^{2} = c^{2}\left(1 - \frac{2GM}{c^{2} r}\right) dt^{2} - \left(1 - \frac{2GM}{c^{2} r}\right)^{-1} dr^{2} - r^{2} d\phi^{2} \]
De metriekvergelijking wordt dan: \[ c^{2}\left(1 - \frac{2GM}{c^{2} r}\right) \left(\frac{dt}{d\tau}\right)^{2} - \left(1 - \frac{2GM}{c^{2} r}\right)^{-1} \left(\frac{dr}{d\tau}\right)^{2} - r^{2}\left(\frac{d\phi}{d\tau}\right)^{2} = c^{2} \]
Na vermenigvuldiging met \( 1 - \frac{2GM}{c^{2} r} \) volgt: \[ c^{2}\left(1 - \frac{2GM}{c^{2} r}\right)^{2} \left(\frac{dt}{d\tau}\right)^{2} - \left(\frac{dr}{d\tau}\right)^{2} - r^{2}\left(\frac{d\phi}{d\tau}\right)^{2} \left(1 - \frac{2GM}{c^{2} r}\right) = c^{2}\left(1 - \frac{2GM}{c^{2} r}\right) \]
Herschikking: \[ \left(\frac{dr}{d\tau}\right)^{2} + r^{2}\left(\frac{d\phi}{d\tau}\right)^{2} \left(1 - \frac{2GM}{c^{2} r}\right) - c^{2}\left(1 - \frac{2GM}{c^{2} r}\right)^{2} \left(\frac{dt}{d\tau}\right)^{2} = c^{2}\left(\frac{2GM}{c^{2} r} - 1\right) \]
We substitueren de behouden grootheden:
\[ \left(1 - \frac{2GM}{c^{2} r}\right)\frac{dt}{d\tau} = \frac{E}{c^{2}}, \qquad r^{2}\frac{d\phi}{d\tau} = L \]
We krijgen dan:
\[ \left(\frac{dr}{d\tau}\right)^{2} + \frac{L^{2}}{r^{2}}\left(1 - \frac{2GM}{c^{2} r}\right) - \frac{E^{2}}{c^{2}} = c^{2}\left(\frac{2GM}{c^{2} r} - 1\right) = \frac{2GM}{r} - c^{2} \]
\[ \left(\frac{dr}{d\tau}\right)^{2} + \frac{L^{2}}{r^{2}}\left(1 - \frac{2GM}{c^{2} r}\right) - \frac{2GM}{r} = c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right) \]
\[ \left(\frac{dr}{d\tau}\right)^{2} + \frac{L^{2}}{r^{2}} = c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right) + \frac{2GM}{r} + \frac{2GM L^{2}}{c^{2} r^{3}} \]
Nu: \[ \frac{dr}{d\tau} = \frac{dr}{d\phi}\frac{d\phi}{d\tau} = \frac{L}{r^{2}}\frac{dr}{d\phi} \]
Dit ingevuld in de vorige vergelijking:
\[ \left(\frac{L}{r^{2}}\frac{dr}{d\phi}\right)^{2} + \frac{L}{r^{2}} = c^{2}\left(\frac{E^{2}}{c^{4}} - 1\right) + 2GM r + \frac{2GM L^{2}}{c^{2} r^{3}} \]
Delen door \(L^{2}\):
\[ \left(\frac{1}{r^{2}}\frac{dr}{d\phi}\right)^{2} + \frac{1}{r^{2}} = \frac{c^{2}}{L^{2}}\left(\frac{E^{2}}{c^{4}} - 1\right) + \frac{2GM}{L^{2} r} + \frac{2GM}{c^{2} r^{3}} \]
Vervang nu door \(u = 1/r\): \[ \frac{du}{d\phi} = \frac{du}{dr}\frac{dr}{d\phi} = -\frac{1}{r^{2}}\frac{dr}{d\phi} \quad\Rightarrow\quad \frac{1}{r^{2}}\frac{dr}{d\phi} = -\frac{du}{d\phi} \]
Nu wordt de vergelijking:
\[ \left(\frac{du}{d\phi}\right)^{2} + u^{2} = \frac{c^{2}}{L^{2}}\left(\frac{E^{2}}{c^{4}} - 1\right) + \frac{2GM}{L^{2}}u + \frac{2GM}{c^{2}}u^{3} \]
We differentiëren deze vergelijking ten opzichte van \( \phi \) om vervolgens te verkrijgen: \[ 2\frac{du}{d\phi}\frac{d^{2}u}{d\phi^{2}} + 2u\frac{du}{d\phi} = \frac{2GM}{L^{2}}\frac{du}{d\phi} + 6\frac{GM}{c^{2}}u^{2}\frac{du}{d\phi} \]
We delen door \(2\,\frac{du}{d\phi}\) (ervan uitgaande dat \(\frac{du}{d\phi} \neq 0\)):
\[ \frac{d^{2}u}{d\phi^{2}} + u = \frac{GM}{L^{2}} + \frac{3GM}{c^{2}}u^{2} \tag{44} \]
Als we de laatste term voorlopig negeren, krijgen we de vergelijking volgens de Newtoniaanse theorie, waarvan de oplossing is: \[ u = \frac{GM}{L^{2}}\left(1 + e\cos\phi\right) \quad\text{of}\quad r = \frac{L^{2}}{GM}\,\frac{1}{1 + e\cos\phi} \tag{45} \]
Dit beschrijft een ellips, waarbij de parameter \(e\) de excentriciteit van de baan voorstelt. Zo kunnen we bijvoorbeeld de baan van een planeet om de zon tekenen. We kunnen de afstand tot het dichtstbijzijnde punt (perihelium) schrijven als \[ r_{1} = a(1 - e) \] en de afstand tot het verst verwijderde punt (aphelium) als \[ r_{2} = a(1 + e). \]
Afgeleid van (45) en wederom gesubstitueerd met \( r = 1/u \) geeft: \[ r = \frac{L^{2}}{GM}\,\frac{1}{1 + e\cos\phi} \quad\Rightarrow\quad r_{\max} = \frac{L^{2}}{GM}\,\frac{1}{1 - e}, \qquad r_{\min} = \frac{L^{2}}{GM}\,\frac{1}{1 + e}. \]
De halve lange as \(a\) wordt dan gegeven door: \[ a = \frac{r_{\max} + r_{\min}}{2} = \frac{L^{2}}{2GM} \left( \frac{1}{1 - e} + \frac{1}{1 + e} \right) = \frac{L^{2}}{2GM} \left( \frac{1 + e + 1 - e}{1 - e^{2}} \right) \]
Dus de bewegingsvergelijking vereist dan dat de halve lange as wordt gegeven door: \[ a = \frac{L^{2}}{GM}\,\frac{1}{1 - e^{2}} \tag{46} \]
Dus: \[ r_{\max} = \frac{L^{2}}{GM}\,\frac{1}{1 - e} = a(1 + e), \qquad r_{\min} = \frac{L^{2}}{GM}\,\frac{1}{1 + e} = a(1 - e). \]
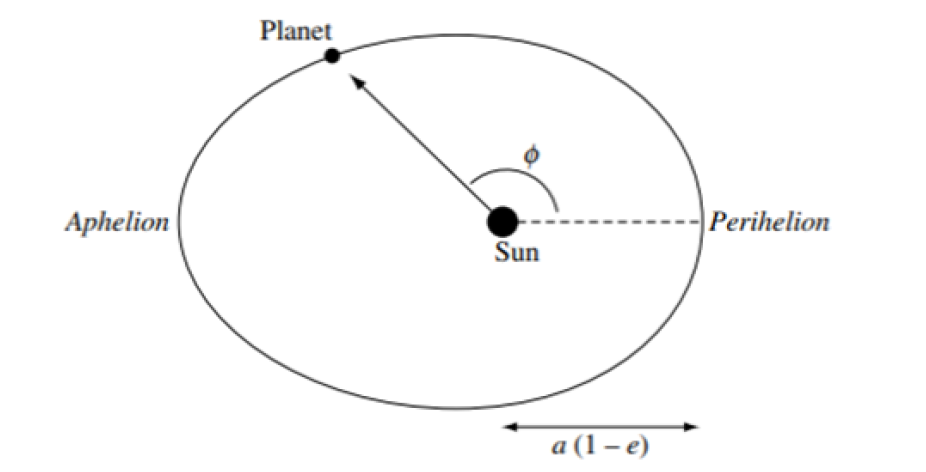
Nu, om de derde term (uit vergelijking 44) op te nemen, wordt de oplossing als volgt: \[ u = \frac{GM}{L^{2}}\left(1 + e\cos\phi\right) + \Delta u \tag{47} \]
\[ \frac{du}{d\phi} = -\frac{GM}{L^{2}}\,e\sin\phi + \frac{d\Delta u}{d\phi}, \qquad \frac{d^{2}u}{d\phi^{2}} = -\frac{GM}{L^{2}}\,e\cos\phi + \frac{d^{2}\Delta u}{d\phi^{2}} \]
Dit substitueren we in formule (44): \[ \frac{d^{2}u}{d\phi^{2}} + u = \frac{GM}{L^{2}} + \frac{3GM}{c^{2}}u^{2} \tag{44} \]
\[ \frac{d^{2}u}{d\phi^{2}} + u = \frac{GM}{L^{2}}\left(1 + e\cos\phi - e\cos\phi\right) + \frac{d^{2}\Delta u}{d\phi^{2}} + \Delta u = \frac{GM}{L^{2}} + \frac{d^{2}\Delta u}{d\phi^{2}} + \Delta u \]
\[ \frac{d^{2}\Delta u}{d\phi^{2}} + \Delta u = -\frac{GM}{L^{2}} + \frac{d^{2}u}{d\phi^{2}} + u = -\frac{GM}{L^{2}} + \frac{GM}{L^{2}} + \frac{3GM}{c^{2}}u^{2} = \frac{3GM}{c^{2}}u^{2} \]
\[ \begin{aligned} \frac{d^{2}\Delta u}{d\phi^{2}} + \Delta u &= \frac{3GM}{c^{2}} \left[ \left(\frac{GM}{L^{2}}\right)^{2} + \left(\frac{GM}{L^{2}} e\cos\phi\right)^2 +\left( \Delta u \right)^2 \right] \\[6pt] &\quad + \frac{3GM}{c^{2}} \left[ 2\left(\frac{GM}{L^{2}}\right)^2 e\cos\phi + 2\frac{GM}{L^{2}}\Delta u + 2\frac{GM}{L^{2}} e\cos\phi\cdot\Delta u \right] \end{aligned} \]We vinden dat, tot de eerste orde in \(\Delta u\): \[ \frac{d^{2}\Delta u}{d\phi^{2}} + \Delta u = \frac{3(GM)^3}{c^{2}L^{4}} \left[1 + \left(e\cos\phi\right)^{2}+2e \cos{\phi}\right] \]
Een bijzondere oplossing van de vergelijking is: \[ \Delta u = \frac{3(GM)^3}{c^{2}L^{4}} \left[1+ e^{2}\left(\frac{1}{2} - \frac{1}{6}\cos(2\phi)\right) + e\phi\sin\phi \right] \tag{48} \]
Dit kan worden gecontroleerd door directe differentiatie van (48): \[ \frac{d\Delta u}{d\phi} = \frac{3(GM)^3}{c^{2}L^{4}} \left[ \frac{1}{3}e^{2}\sin(2\phi) + e\sin\phi + e\phi\cos\phi \right] \]
\[ \frac{d^{2}\Delta u}{d\phi^{2}} = \frac{3(GM)^3}{c^{2}L^{4}} \left[ \frac{2}{3}e^{2}\cos(2\phi) + e\cos\phi + e\cos\phi - e\phi\sin\phi \right] \]
Invullen in (48): \[ \frac{d^{2}\Delta u}{d\phi^{2}} + \Delta u = \frac{3(GM)^3}{c^{2}L^{4}} \left[ \frac{2}{3}e^{2}\cos(2\phi) + 2e\cos\phi - e\phi\sin\phi+1+ e^2\left( \frac{1}{2}-\frac{1}{6}\cos(2\phi)\right) + e\phi\sin\phi \right] \]
\[ \frac{d^{2}\Delta u}{d\phi^{2}} + \Delta u = \frac{3(GM)^3}{c^{2}L^{4}} \left(1 + \tfrac{1}{2}e^{2} + \tfrac{1}{2}e^{2}\cos 2\phi + 2e\cos\phi\right) \]
\[ \frac{d^{2}\Delta u}{d\phi^{2}} + \Delta u = \frac{3(GM)^3}{c^{2}L^{4}} \left[1 + \frac{1}{2}e^{2}\left(1 + \cos 2\phi\right)+2e\cos\phi\right] \]
\[ \frac{d^{2}\Delta u}{d\phi^{2}} + \Delta u = \frac{3(GM)^3}{c^{2}L^{4}} \left[ 1 + \frac{1}{2}e^{2}\left(\sin^{2}\phi + \cos^{2}\phi + \cos^{2}\phi - \sin^{2}\phi\right) + 2e\cos\phi \right] \]
\[ \frac{d^{2}\Delta u}{d\phi^{2}} + \Delta u = \frac{3(GM)^3}{c^{2}L^{4}} \left(1 + e^{2}\cos^2\phi + 2e\cos\phi\right) \]
Dus, vergelijking (44) is correct.
Nu vullen we \(\Delta u\) in vergelijking (3) in: \[ u = \frac{GM}{L^{2}}\left(1 + e\cos\phi\right) + \Delta u \]
\[ u = \frac{GM}{L^{2}}\left(1 + e\cos\phi\right) + \frac{3(GM)^3}{c^{2}L^{4}} \left[1+e^{2}\left(\frac{1}{2}-\frac{1}{6}\cos{2\phi} \right)+e\phi\sin{\phi} \right] \]
\[ u = \frac{GM}{L^{2}}\left(1 + e\cos\phi\right) + \frac{3(GM)^3}{c^{2}L^{4}}\,e\,\phi\sin\phi + \frac{3(GM)^3}{c^{2}L^{4}} \left[1 + e^{2}\left(\frac{1}{2} - \frac{1}{6}\cos 2\phi\right) \right] \]
Aangezien de constante \[ \frac{3GM}{c^{2}L^{4}} \] erg klein is, kunnen de laatste drie termen aan de rechterkant worden verwaarloosd — ze zijn te klein om meetbare invloed te hebben.
Toch is de laatste term \[ e\,\frac{3(GM)^3}{c^{2}L^{4}}\,\phi\sin\phi \] een speciaal geval: hoewel klein, groeit hij langzaam met \(\phi\), omdat \(\phi\) zelf blijft toenemen. Het effect stapelt zich op en moet daarom behouden blijven.
\[ u = \frac{GM}{L^{2}}\left[1 + e\left(\cos\phi+ \frac{3(GM)^2}{c^{2}L^{2}}\, \phi\sin\phi\right)\right] + \frac{3(GM)^3}{c^{2}L^{4}}\left[1+e^2\left(\frac{1}{2}- \frac{1}{6}\cos 2\phi\right) \right] \]
Dus, onze benaderde oplossing is: \[ u = \frac{GM}{L^{2}}\left[ 1 + e\left(\cos\phi+\frac{3(GM)^2}{2c^{2}L^{2}}\,\phi\sin\phi\right) \right] \]
Met behulp van de relatie: \[ \cos\left[\phi(1 - \frac{3(GM)^2}{c^{2}L^{2}})\right] = \cos\left(\phi - \frac{3(GM)^2}{c^{2}L^{2}}\phi\right) =\cos{\phi}\cos{\frac{3(GM)^2}{c^{2}L^{2}}}\phi+\sin{\phi}\sin{\frac{3(GM)^2}{c^{2}L^{2}}}\phi \]
en de benadering \[ \cos(A - \epsilon A) \approx \cos A + \epsilon A \sin A \quad\text{voor}\quad \epsilon \ll 1, \] wordt het resultaat: \[ \approx\cos{\phi}+\frac{3(GM)^2}{c^{2}L^{2}}\phi\sin{\phi}\quad voor \quad \frac{3(GM)^2}{c^{2}L^{2}} \ll 1 \]
en kunnen we nu schrijven: \[ u \approx \frac{GM}{L^{2}}\left\{1+ecos{\left[\phi\left(1-\frac{3(GM)^2}{c^{2}L^{2}}\right)\right] }\right\} = \frac{GM}{L^{2}}\left\{ 1 + e\cos{\left[\phi(1 - \epsilon)\right]} \right\} \]
waarbij \[ \epsilon = \frac{3(GM)^2}{c^{2}L^{2}}. \]
Voor \( r = 1/u \) krijgen we: \[ r = \frac{L^{2}}{GM\,\left\{1 + e\cos{\left[\phi(1 - \epsilon)\right]}\right\}} \tag{5} \]
Uit deze uitdrukking blijkt dat de baan weliswaar periodiek is, maar met een periode \[ \frac{2\pi}{1 - \epsilon}. \] Dit betekent dat de waarden van \( r \) zich herhalen in een hoek die groter is dan \( 2\pi \). Hierdoor sluit de baan niet perfect zoals bij een klassieke ellips: de ellips draait langzaam rond het brandpunt. Dit verschijnsel noemen we precessie.
Na elke volledige omloop is de ellips iets verdraaid rond het focuspunt, en wel met een hoek: \[ \Delta\phi = \frac{2\pi}{1 - \epsilon} - 2\pi = \frac{2\pi\epsilon}{1 - \epsilon} \approx 2\pi\epsilon = \frac{6\pi (GM)^2}{c^{2}L^{2}}. \]
We vervangen \(L\) met behulp van vergelijking (2): \[ a = \frac{L^{2}}{GM}\,\frac{1}{1 - e^{2}} \tag{2} \]
Door deze uitdrukking te substitueren in vergelijking (5): \[ r = \frac{L^{2}}{GM\,\left\{1 + e\cos{\left[\phi(1 - \epsilon)\right]}\right\}} \tag{5} \] krijgen we voor het baantraject: \[ r = \frac{a(1 - e^{2})}{1 + e\cos\left[\phi(1-\epsilon)\right]} \tag{5a} \]
Met: \[ \epsilon = \frac{3(GM)^2}{c^{2}L^{2}} \qquad\text{of}\qquad \epsilon = \frac{3(GM)^2}{c^2GM\,a(1 - e^{2})} = \frac{3GM}{c^{2}a(1 - e^{2})}. \]
Afgeleid uit de derde wet van Kepler: \[ T^{2} = \frac{4\pi^{2}a^{3}}{G(M + m)} \approx \frac{4\pi^{2}a^{3}}{GM} \quad\Rightarrow\quad T = 2\pi\,a\,\sqrt{\frac{a}{GM}}. \]
Voor de snelheid \(v\): \[ v = \frac{L}{r\cos\alpha} = \frac{\sqrt{aGM(1 - e^{2})}}{a(1 - e^{2})}\, \,\frac{1 + e\cos\left[\phi(1-\epsilon)\right]}{\cos\alpha}\, \]
Dus: \[ v = \sqrt{\frac{GM}{a(1 - e^{2})}}\, \,\frac{1 + e\cos\left[\phi(1-\epsilon)\right]}{\cos\alpha}\, \]
waarbij: \[ \epsilon = \frac{3(GM)^2}{c^{2}L^{2}} =\frac{3(GM)^2}{c^2aGM(1 - e^{2})} = \frac{3GM}{c^{2}a(1 - e^{2})}. \]
Omdat: \[ L^{2} = aGM(1 - e^{2}), \]
ingevuld geeft: \[ \Delta\phi = \frac{6\pi (GM)^2}{c^{2}aGM(1 - e^{2})}. \]
Uiteindelijk krijgen we voor de precessiehoek: \[ \Delta\phi = \frac{6\pi GM}{a(1 - e^{2})c^{2}} \tag{6} \]
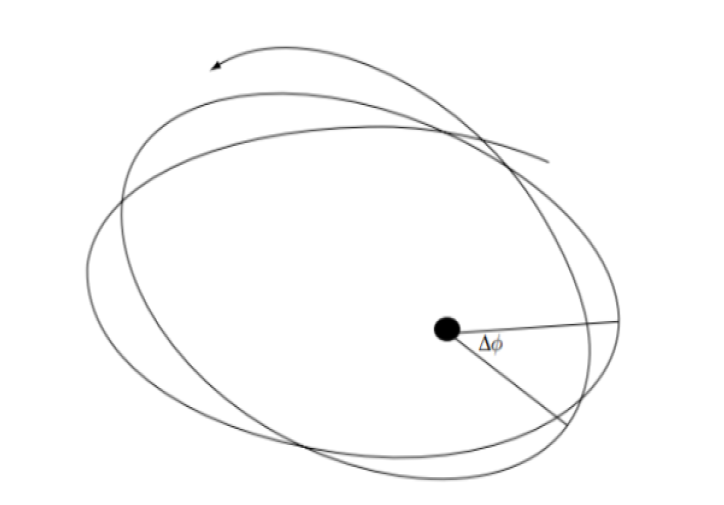
We passen vergelijking (6) toe op de baan van Mercurius, met de volgende parameters:
- periode = 88 dagen
- \( a = 5.8 \times 10^{10}\,\text{m} \)
- e = 0.2
- \(M_s = 2 \times 10^{30}\,\text{kg}\)
vinden we: \[ T = \sqrt{\frac{4\pi^{2} a^{3}}{GM}} = 87.95\ \text{dagen} \] \[ \Delta\phi = \frac{6\pi GM}{a(1 - e^{2})c^{2}} = 5.02 \times 10^{-7}\ \text{rad per omwenteling} \]
Om de precessie per eeuw te berekenen: \[ \Delta\phi = 5.02 \times 10^{-7} \times \left(100 \times \frac{365.25}{88}\right) \times \left(\frac{360 \times 60 \times 60}{2\pi}\right) \] \[ \Delta\phi = 43''\ \text{boogseconden per eeuw}. \]
In werkelijkheid is de gemeten precessie: \[ 5599''.7 \pm 0.4''\ \text{per eeuw}. \]
Het overgrote deel hiervan wordt veroorzaakt door gravitatie‑invloeden van andere planeten. Maar na correctie voor deze verstoringen blijft er een restafwijking over die verrassend goed overeenkomt met de voorspelling van de algemene relativiteitstheorie.
Voor andere hemellichamen vinden we vergelijkbare resultaten (in boogseconden per eeuw):
| Object | Waargenomen restprecessie | Voorspelde restprecessie |
|---|---|---|
| Mercurius | 43.1 ± 0.5 | 43.03 |
| Venus | 8 ± 5 | 8.6 |
| Aarde | 5 ± 1 | 3.8 |
| Icarus | 10 ± 1 | 10.3 |
De resultaten komen dus uitstekend overeen met de voorspellingen van de algemene relativiteitstheorie. Einstein voegde deze berekening voor Mercurius toe aan zijn artikel uit 1915 over de algemene relativiteitstheorie. Hiermee loste hij direct een van de grote openstaande problemen in de klassieke hemelmechanica op – een indrukwekkende eerste toets van zijn nieuwe, complexe theorie. Je kunt je voorstellen hoeveel vertrouwen dit hem gaf in de juistheid ervan.
4.8 Experiment 6 - Berekening van een Kogelbaan
Als oefening zijn we geïnteresseerd in het berekenen van de baan van een kogel met behulp van de regels van de algemene relativiteitstheorie, in tegenstelling tot de klassieke (Newtoniaanse) benadering.
Voor de benadering volgens de Algemene Relativiteit veronderstellen we dat de baan van de kogel door de massa van de Aarde gedwongen wordt om een elliptische vorm te volgen. Voor de berekening maken we gebruik van de Schwarzschild-vergelijking. Maar eerst beginnen we met de Newtoniaanse benadering.
4.8.1 Newtoniaanse Benadering
We beschouwen een kogel die onder een hoek wordt afgevuurd, met een horizontale afstand D tussen het startpunt en het doelwit, en een maximale hoogte h. De zwaartekrachtsversnelling is g, en de initiële snelheid van de kogel heeft componenten vx0 (horizontaal) en vy0 (verticaal).
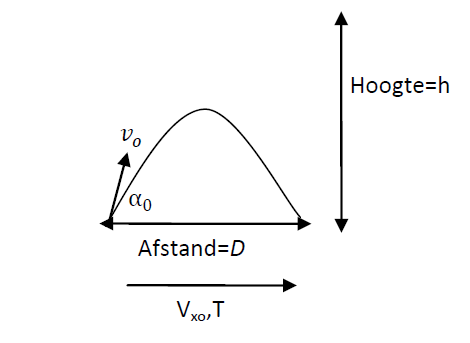
a) Tijd en snelheidscomponenten
De tijd die de kogel nodig heeft om de afstand D af te leggen met de constante horizontale snelheid vx0 is:
\[ v_{x0} = \frac{D}{T} \quad \Rightarrow \quad T = \frac{D}{v_{x0}} \]Om de afstand D af te leggen, heeft de kogel ook een opwaartse snelheid nodig, anders raakt hij te vroeg de grond. Dit vereist een initiële snelheidscomponent in de y-richting vy0. Deze snelheid wordt bepaald door de horizontale afstand D en de tijd T. Dus T is ook de tijd die het kost om vanaf de grond omhoog te gaan en weer terug naar de grond te vallen.
Omdat de beweging symmetrisch is, is de tijd om het hoogste punt te bereiken:
\[ T_{\text{omhoog}} = \frac{T}{2} \]Op dit punt is de verticale snelheid nul. Uit de bewegingsvergelijking volgt:
\[ v_y = v_{y0} - g t = 0 \quad \text{bij} \quad t = \frac{T}{2} \]Hieruit volgt:
\[ v_{y0} = g t = g \frac{T}{2} = g \frac{D}{2 v_{x0}} \]b) Hoogte en relatie met tijd
De maximale hoogte wordt bereikt op tijdstip T/2, dus:
\[ h = v_{y0} \frac{T}{2} - \frac{1}{2} g \left( \frac{T}{2} \right)^2 \] \[ h = \frac{g D}{2 v_{x0}} \cdot \frac{D}{2 v_{x0}} - \frac{1}{2} g \left( \frac{D}{2 v_{x0}} \right)^2 = \frac{g D^2}{8 v_{x0}^2} \]Omgekeerd geeft dit:
\[ v_{x0} = D \sqrt{\frac{g}{8h}} \]Wanneer de kogel van het hoogste punt h terugvalt, duurt het T/2 om de grond te bereiken.
c) Totale snelheid en baanparameters
Om het hoogste punt te bereiken geldt:
\[ v_{y0} = g \frac{T}{2} = g \sqrt{\frac{2h}{g}} = \sqrt{2 h g} \]De totale beginsnelheid is:
\[ v_0^2 = v_{x0}^2 + v_{y0}^2 = \frac{g D^2}{8 h} + 2 h g = g \frac{D^2 + 16 h^2}{8 h} \] \[ \Rightarrow v_0 = \sqrt{ g \frac{D^2 + 16 h^2}{8 h} } \]Verder geldt:
\[ v_{x0} = v_0 \cos \alpha_0 \]De hellingshoek α0 waaronder de kogel wordt afgevuurd volgt uit:
\[ \tan \alpha_0 = \frac{v_{y0}}{v_{x0}} = \frac{\sqrt{2 h g}}{D \sqrt{g/(8h)}} = \frac{4 h}{D} \] \[ \tan \alpha_0 = \frac{4 h}{D} \]d) Baanvergelijking
De y-positie als functie van de tijd:
\[ y(t) = v_{y0} t - \frac{1}{2} g t^2 = g \frac{T}{2} t - \frac{1}{2} g t^2 = \frac{1}{2} g t (T - t) \] \[ y(t) = \frac{1}{2} g t \left( \frac{D}{v_{x0}} - t \right) \]In termen van de x-positie:
\[ x = v_{x0} t \quad \Rightarrow \quad t = \frac{x}{v_{x0}} \] \[ y(x) = \frac{1}{2} g \frac{x}{v_{x0}} \left( \frac{D}{v_{x0}} - \frac{x}{v_{x0}} \right) = \frac{1}{2} \frac{g}{v_{x0}^2} x (D - x) \]De baan van de kogel is dus een parabool:
\[ y(x) = \frac{1}{2} \frac{g}{v_{x0}^2} x (D - x) \]Dit is dus een functie van de vereiste afstand D wanneer de initiële horizontale snelheidscomponent \(v_{x0}\) is.
e) Voorbeeldberekening
| D (m) | vx0 (m/s) | T (s) | h (m) | v0 (m/s) |
|---|---|---|---|---|
| 10 | 5 | 2 | 4.93 | 11.06 |
| 10 | 500 | 0.02 | 0.000493 | 500 |
| 100 | 5 | 20 | 493 | 99 |
| 100 | 50 | 2 | 4.93 | 51 |
(welke zijn berekend met g = 9,87 m/s²)
f) Volgende stap
Nu we de Newtoniaanse benadering volledig hebben uitgewerkt, kunnen we deze vergelijken met de berekening op basis van de Schwarzschild-geometrie binnen de algemene relativiteitstheorie. Deze vergelijking volgt in de volgende sectie.
4.8.2 Schwarzschild-Benadering
Voor deze benadering beschouwen we de kogelbaan als een deel van een ellips, waarbij het middelpunt van de aarde samenvalt met een van de brandpunten. We gebruiken de resultaten uit de Schwarzschild-vergelijking uit hoofdstuk 4.7, Alternatieve Afleiding van de Baanvergelijking.
Voor het baantraject geldt dat de semi-grote as:
\[ a = \frac{L^2}{G M} \frac{1}{1 - e^2} \tag{2} \]De parameter e is de excentriciteit van de kogelbaan. Het perihelium is:
\[ r_1 = a (1 - e) \]en het aphelium:
\[ r_2 = a (1 + e) \] \[ e = \sqrt{1 - b^2 c^2} = \frac{r_2 - r_1}{r_2 + r_1} \]Voor een cirkel geldt dus \(e = 0\,\, \text{en} \,\,r = r_1 = r_2 = a\).
Voor een ellips met het middelpunt van de aarde in de linker focus geldt:
\[ r(\phi) = \frac{a (1 - e^2)}{1 - e \cos\!\left[\phi(1-\epsilon)\right]} \tag{2a} \]Hoek tussen snelheid en straalvector
We bepalen nu de hoek \(α\) tussen de snelheid \(v\) (tangentaal aan de ellips) en de loodrechte component \(v_{per}\) om het impulsmoment te bepalen. In dit experiment is \(v\) de totale snelheid van de kogel langs de ellips, terwijl \(v_{per}\) de component van de snelheid 𝑣 is ten opzichte van het aardoppervlak en zoals vermeld loodrecht op \(r(\phi)\).
\[ \tan \alpha = \frac{1}{r} \frac{dr}{d\phi} \] \[ \tan \alpha =\frac{\{1-e\cos\left[\phi(1-\epsilon)\right]\}}{a(1-\epsilon^2)}\, \frac{\{a(1-e^2)(1-\epsilon)(e\sin{\left[\phi(1-\epsilon)\right])}\}} {\{1-e\cos\left[\phi(1-\epsilon)\right]\}^2} \] \[ \tan \alpha =\frac{dr}{rd\phi} =\frac{e(1-\epsilon)\sin{\left[\phi(1-\epsilon)\right]}}{1 - e \cos\left[\phi(1-\epsilon)\right]} \] \[ \alpha = \arctan\left(\frac{e(1-\epsilon)\sin{\left[\phi(1-\epsilon)\right]}} {1 - e \cos\left[\phi(1-\epsilon)\right]} \right) \]Met:
\[ \cos \alpha = \frac{1}{\sqrt{1 + \tan \alpha}} \]Dan krijgen we:
\[ cos{\alpha}=\left[1+ \left( \frac{e(1-\epsilon)\sin{\left[\phi(1-\epsilon)\right]}} {1 - e \cos\left[\phi(1-\epsilon)\right]} \right)^2\right]^{-1/2} \] \[ cos{\alpha}=\left[ \frac{ 1 - 2 e \cos\left[\phi(1-\epsilon)\right] + e^2 \cos^2\left[\phi(1-\epsilon)\right] + \{e(1-\epsilon)\sin\left[\phi(1-\epsilon)\right] \}^2 }{\{1 - e \cos\left[\phi(1-\epsilon)\right]\}^2} \right]^{-1/2} \]Vanwege het negatieve wortelteken draaien we de vergelijking om:
\[ cos{\alpha}= \frac{1 - e \cos\left[\phi(1-\epsilon)\right]}{\left[ 1 - 2 e \cos\left[\phi(1-\epsilon)\right] + e^2 \cos^2\left[\phi(1-\epsilon)\right] + (1-2\epsilon+\epsilon^2)e^2\sin^2\left[\phi(1-\epsilon)\right]\right]^{1/2}} \] \[ cos{\alpha}= \frac{1 - e \cos\left[\phi(1-\epsilon)\right]}{\left[ 1 - 2 e \cos\left[\phi(1-\epsilon)\right] + e^2 \cos^2\left[\phi(1-\epsilon)\right] +e^2\sin^2\left[\phi(1-\epsilon)\right]-\epsilon (2-\epsilon)e^2\sin^2\left[\phi(1-\epsilon)\right]\right]^{1/2}} \] \[ cos{\alpha}= \frac{1 - e \cos\left[\phi(1-\epsilon)\right]} {\left[ 1 - 2 e \cos\left[\phi(1-\epsilon)\right] +e^2(1-\epsilon (2-\epsilon)\sin^2\left[\phi(1-\epsilon)\right])\right]^{1/2}} \tag{2b} \]Impulsmoment
Het impulsmoment L is constant langs de ellips en wordt gegeven door:
\[ L = v_{per}\cdot r = v \cdot \cos \alpha \cdot \, r \]Op het startpunt aan het aardoppervlak geldt:
\[ L = v_{x0}\cdot R_{\text{earth}} \]Volgens de Schwarzschild-oplossing:
\[ L = \sqrt{a G M (1 - e^2)} \]Snelheid langs de ellips
\[ v = \frac{L}{r \cos \alpha} = \frac{\sqrt{aG M(1 - e^2)}}{a(1-e^2)\,\cos{\alpha}} (1-e\cos\left[\phi(1-\epsilon)\right]) \]Dit vereenvoudigt tot:
\[ v = \sqrt{\frac{G M}{a (1 - e^2)}}\, \frac{1 - e \cos\!\left[\phi(1-\epsilon)\right])} {\cos \alpha} \tag{2c} \]Vul \(\cos{\alpha}\) uit vergelijking (2b) in vergelijking (2c) in:
\[ v = \left(\frac{G M}{a (1 - e^2)}\right)^{1/2}\,\frac{1-e\cos\left[\phi(1-\epsilon)\right]}{1-e\cos\left[\phi(1-\epsilon)\right]} (1 - 2 e \cos\!\left[\phi(1-\epsilon)\right] + e^2\{1-\epsilon(2-\epsilon) \sin^2\!\left[\phi(1-\epsilon)\right]\})^{1/2} \]De ogenblikkelijke snelheid als functie van \(\phi\) is:
\[ v = \sqrt{\left(\frac{G M}{a (1 - e^2)}\right)\, (1 - 2 e \cos\!\left[\phi(1-\epsilon)\right] + e^2\{1-\epsilon(2-\epsilon) \sin^2\!\left[\phi(1-\epsilon)\right]\})} \tag{2d} \]Relativistische correctieparameter
Verkregen uit het vorige hoofdstuk \(\epsilon\):
\[ \epsilon = \frac{3 (G M)^2}{c^2 L^2} = \frac{3 (G M)^2}{c^2 aGM(1-e^2)} = \frac{3 G M}{c^2 a (1 - e^2)} \]Hier is:
\[ \epsilon = \frac{3 (G M)^2}{c^2 L^2} = \frac{3 (G M)^2}{c^2 (v_{x0}R_{earth})^2} = \frac{3c^2}{v_{x0}^2} \left( \frac{G M}{c^2 R_{earth}} \right)^2 \,\,\text{deze is dimensieloos} \tag{2e} \]Geometrische relaties
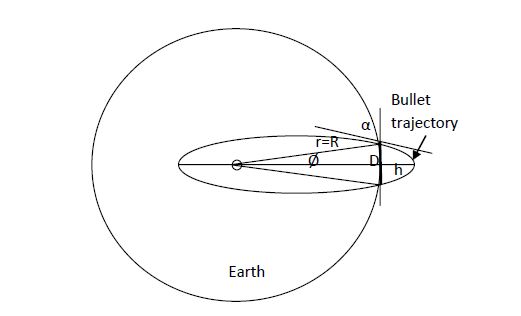
Om iets verder in te zoomen:
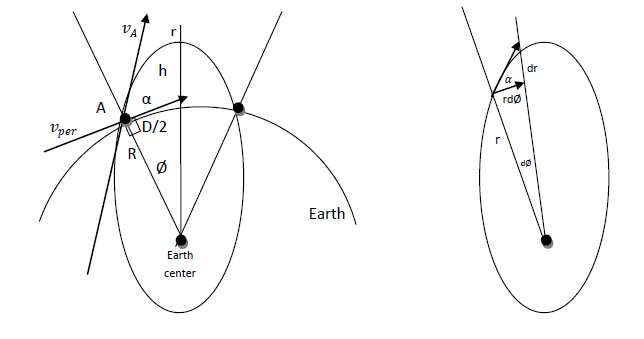
\[ \phi \cdot R=\frac{D}{2} \Rightarrow \phi=\frac{D}{2R} \] \[ v_{per} = v_{xA} = v\cos(\alpha) \,\,\text{en}\,\, v_{yA} = v\sin(\alpha) \]
Uit (2a): \[ a(1 - e^{2}) = r\{1 - e\cos\left[\phi\,(1 - \epsilon)\right]\} \]
Uit (2d):\[ v = \sqrt{\left(\frac{G M}{a (1 - e^2)}\right)\, (1 - 2 e \cos\!\left[\phi(1-\epsilon)\right] + e^2\{1-\epsilon(2-\epsilon) \sin^2\!\left[\phi(1-\epsilon)\right]\})} \] \[ v^2 = \left(\frac{G M}{a (1 - e^2)}\right)\, (1 - 2 e \cos\!\left[\phi(1-\epsilon)\right] + e^2\{1-\epsilon(2-\epsilon) \sin^2\!\left[\phi(1-\epsilon)\right]\}) \] \[ v^2 =GM \,\frac{ (1 - 2 e \cos\!\left[\phi(1-\epsilon)\right] + e^2\{1-\epsilon(2-\epsilon) \sin^2\!\left[\phi(1-\epsilon)\right]\}) }{r\{1 - e \cos\!\left[\phi(1-\epsilon)\right]\}} \] \[ \frac{v^2r}{GM}\,\{1 - e \cos\left[\phi(1-\epsilon)\right]\}= 1 - 2 e \cos\!\left[\phi(1-\epsilon)\right] + e^2\{1-\epsilon(2-\epsilon) \sin^2\!\left[\phi(1-\epsilon)\right]\} \] \[ e^2\{1-\epsilon(2-\epsilon) \sin^2\!\left[\phi(1-\epsilon)\right]\}- e \cos\left[\phi(1-\epsilon)\right]\left(2-\frac{v^2r}{GM}\right) +\left(1-\frac{v^2r}{GM}\right)=0 \] \[ e=\frac{\cos\left[\phi(1-\epsilon)\right]\left(2-\frac{v^2r}{GM}\right)\pm \sqrt{ \left[\cos \left[\phi(1-\epsilon)\right]\left(2-\frac{v^2r}{GM}\right)\right]^2-4\left(1-\frac{v^2r}{GM}\right) \{1-\epsilon(2-\epsilon) \sin^2\!\left[\phi(1-\epsilon)\right]\}\ }} {2\{1-\epsilon(2-\epsilon) \sin^2\!\left[\phi(1-\epsilon)\right]\}} \]
Voor het startpunt bij het snijpunt van de aarde en de baan geldt dat \(r=R\). (\(R\) is hier de
straal van de aarde) en \(\phi=\frac{D}{2R}\).
Uit (2a):
Of hier uit de vergelijkingen (2), (2e) en (3):
\[ R\left\{1 - e\cos\left[\frac{D}{2R}(1 - \epsilon)\right]\right\} = a(1 - e^{2}) = \frac{L^{2}}{GM} \]
\[ e=\frac{1-\frac{L^{2}}{RGM}}{\cos\left[\frac{D}{2R}(1 - \epsilon)\right]}= \frac{1-\frac{L^{2}}{RGM}}{\cos\left[\frac{D}{2R}\left(1 - \frac{3c^2}{v_{x0}^2}\left(\frac{GM} {c^2R_{earth}}\right)^2\right)\right]} = \frac{1-\frac{(v_{x0}R)^{2}}{RGM}}{\cos\left[\frac{D}{2R}\left(1 - \frac{3c^2}{v_{x0}^2}\left(\frac{GM} {c^2R_{earth}}\right)^2\right)\right]} \] \[ e= \frac{1-\frac{(v_{x0}R)^{2}}{RGM}}{\cos\left[\frac{D}{2R}\left(1 - \frac{3c^2}{v_{x0}^2}\left(\frac{GM} {c^2R_{earth}}\right)^2\right)\right]} \]De gegeven snelheid op het punt \( r = R \) is \( v \). Dus voor een gegeven snelheid zijn er twee oplossingen voor \( e \).
Hier is \( h \) het hoogste punt van de kogelbaan: \[ h = a(1 + e) - R \]
Samen met (3): \[ h = \frac{R\left\{1 - e\cos\left[\frac{D}{2R}\left(1 - \epsilon\right)\right]\right\}} {1 - e^{2}}(1 + e) - R= R\left\{\frac{1 - e\cos\left[\frac{D}{2R}\left(1 - \epsilon\right)\right]} {1 - e} - 1\right\} \] \[ h = R\left\{\frac{1 - e\cos\left[\frac{D}{2R}\left(1 - \epsilon\right)\right]-1+\epsilon} {1 - e}\right\} = R\frac{e\left(1 - e\cos\left[\frac{D}{2R}\left(1 - \epsilon\right)\right]\right)} {1 - e} \]
Hier is \( D \) de horizontale afstand van de kogel op aarde, \( v \) is de startsnelheid van de kogel en \( R \) is de aardstraal. Zoals hierboven gezien is: \[ \phi = \frac{D}{2R}. \]
Of pragmatisch gezien, in ons kogelvoorbeeld met \( v_{x0} \) en \( D \) als startpunten:
\[ h = a(1 + e) - R = a\frac{1 - e^{2}}{1 - e} - R = \frac{L^{2}}{GM}\frac{1}{1 - e} - R \]
\[ = \frac{v_{x0}^{2} R^{2}}{GM}\frac{1}{1 - e} - R \]
Waarbij: \[ e = \frac{1 - \frac{v_{x0}^{2} R}{GM}}{\cos\left[\frac{D}{2R} \left(1 - \frac{3c^{2}}{v_{x0}^{2}}\left(\frac{GM}{ c^{2} R}\right)^2\right)\right]} \]
Afleiding van de omtrek van een ellips
\[ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1, \qquad x = a\cos\beta,\quad y = b\sin\beta \]
\[ \text{Omtrek} = 4a \int_{0}^{\pi/2} \sqrt{ \left(\frac{dx}{d\beta}\right)^{2} + \left(\frac{dy}{d\beta}\right)^{2} } \, d\beta \]
\[ = 4a \int_{0}^{\pi/2} \sqrt{ a^{2}\sin^{2}\beta + b^{2}\cos^{2}\beta } \, d\beta \]
\[ = 4a \int_{0}^{\pi/2} \sqrt{ a^{2}(1-\cos^2\beta) + b^{2}\cos^{2}\beta } \, d\beta \]
\[ = 4a \int_{0}^{\pi/2} \sqrt{ a^{2} - (a^{2} - b^{2})\cos^{2}\beta } \, d\beta \]
\[ \text{Omtrek} = 4a \int_{0}^{\pi/2} \sqrt{ 1 - e^{2}\cos^{2}\beta } \, d\beta \]
Voor de omtrek van een ellips bestaat geen eenvoudige gesloten oplossing. Een bekende benadering is de Ramanujan‑formule:
\[ \text{Omtrek} \approx \pi a \left[ 3(1 + \sqrt{1 - e^{2}}) - \sqrt{10\sqrt{1 - e^{2}} + 3(2 - e^{2})} \right] \]
Samenvatting van gebruikte formules
De vertrekpunten voor deze afleiding zijn de snelheid van de kogel langs het aardoppervlak (\(v_{x0}=v_{per}\) loodrecht op \(𝑟\)) en de vereiste afstand \(D\). Dus, op het startpunt waar de kogel is gelanceerd, kennen we de positie en de impuls van de kogel en zouden we in staat moeten zijn om de baan te berekenen.
- \( L = v_{x0}\cdot R_{\text{Earth}} \hspace{13em}\text{dus}\,\,\epsilon\, \text{is L functie van }L\left(v_{x0}\right) \)
- \( \epsilon = \dfrac{3 (G )^2M}{2 c^2 L^2} \hspace{14em}\text{dus}\,\,\epsilon\left(v_{x0}\right) \)
- \( \phi = \dfrac{D}{2R} \hspace{16em}\text{dus}\,\,\phi\left(D\right)\)
- \( e = \dfrac{1 - \frac{L^{2}}{RGM}} {\cos\!\left[\phi(1 - \epsilon)\right]} \hspace{12em}\text{dus}\, \,e\left(v_{x0},D\right)\)
- \( \alpha = \arctan\!\left\{ \dfrac{e\,(1 - \epsilon)\sin\left[\phi(1 - \epsilon)\right]} {1 - e\,\cos\left[\phi(1 - \epsilon)\right]} \right\} \hspace{4em}\text{dus}\,\,e\left(v_{x0},D\right) \)
- \( a = \dfrac{L^2}{G M (1-e^2)} \hspace{12em}\text{dus}\,\,a\left(v_{x0},D\right) \)
- \( h = a(1+e) - R \hspace{12em} \text{dus}\,\,h\left(v_{x0},D\right) \)
Met deze formules kunnen, uitgaande van de startsnelheid en de vereiste afstand, de volledige baan en het hoogste punt van de kogel relativistisch worden berekend.
Gedetailleerde resultaten van berekeningen
Gedetailleerde resultaten van berekeningen voor het bovengenoemde voorbeeld. De startpunten zijn de (loodrecht op r) snelheid van de kogel en de af te leggen afstand.
| Newton | Schwarzschild | |||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | 5 m/s | 500 m/s | 500 m/s | 1000 m/s | 5 m/s | 500 m/s | 500 m/s | 1000 m/s |
| Afstand (m) | 10 | 10 | 2000 | 2000 | 10 | 10 | 2000 | 2000 |
| vr0 (m/s) | 9.87 | 0.10 | 19.73 | 9.87 | 9.76 | 0.10 | 19.66 | 9.71 |
| Snelheid (m/s) | 11 | 500 | 500 | 1000 | 11 | 500 | 500 | 1000 |
| \(\epsilon\) | - | - | - | - | 5.25×10-3 | 5×10-7 | 5.25×10-7 | 1×10-7 |
| e (excentriciteit) | – | – | – | – | 1.000 | 0.996 | 0.996 | 0.984 |
| a (m) | – | – | – | – | 3.18×106 | 3.18×106 | 3.18×106 | 3.20×106 |
| h (m) | 4.93 | 4.93×10-4 | 19.73 | 4.93 | 4.88 | 4.91×10-4 | 19.66 | 4.85 |
| α (rad) | 1.10 | 0.000 | 0.04 | 0.010 | 1.10 | 0.000 | 0.04 | 0.010 |
| α (deg) | 63.13 | 0.0113 | 2.26 | 0.565 | 62.88 | 0.0113 | 2.25 | 0.556 |
| Φ (rad) | – | – | – | – | 7.87×10-7 | 7.87×10-7 | 1.57×10-4 | 1.57×10-4 |
| L (impulsmoment) | 3.18×107 | 3.18×109 | 3.18×109 | 6.36×109 | 3.18×107 | 3.18×109 | 3.18×109 | 6.36×109 |
| cos(α) | 0.4520 | 1.0000 | 0.9992 | 1.0000 | 0.4558 | 1.0000 | 0.9992 | 1.0000 |
| cos(α + Φ) | – | – | – | – | 0.4558 | 1.000 | 0.9992 | 1.000 |
| Omtrek (km) | - | - | - | - | 12662 | 12894 | 12894 | 13346 |
3) Analyse van de resultaten
Hoogteverschillen
In het klassieke geval is de maximale hoogte van het projectiel \( h \approx 4.93 \,\text{m} \) bij lage snelheden. In de Schwarzschild-benadering is deze licht lager (bijvoorbeeld \( h \approx 4.88 \,\text{m} \)), wat wijst op een sterkere effectieve zwaartekracht.
Excentriciteit
Een excentriciteit van exact \( e = 1 \) impliceert de klassieke parabool. De Schwarzschild-benadering toont dat de banen licht elliptisch zijn met \( e < 1. \) Voor een horizontale snelheid van 500 m/s blijkt \( e \approx 0.996, \) terwijl bij 5 m/s \( e \approx 1, \) wat overeenkomt met een bijna-parabolische baan.
Richtingshoek
De afwijking in richtingshoek \( \Phi \) is zeer klein bij lage snelheden, maar meetbaar bij hogere energieën. Voor een projectiel van 500 m/s over 2 km bedraagt de afwijking \( \Phi \approx 1.57 \times 10^{-4} \,\text{rad}, \) wat overeenkomt met een precessie van de ellips-as.
Impulsmoment en cirkelomtrek
Het impulsmoment \( L \) neemt toe met de beginsnelheid. De bijbehorende (benaderde) omtrek van de elliptische baan toont eveneens een toename, wat de langere afgelegde weg van een krachtig projectiel weerspiegelt.
4.8.3 Conclusie
- Newtoniaanse ballistiek is een uitstekende benadering voor dagelijkse situaties.
- Relativistische correcties zijn subtiel, maar onmisbaar voor zeer nauwkeurige toepassingen en bij hoge snelheden.
- De Schwarzschild-benadering toont dat zelfs een simpele kogelbaan in principe beïnvloed wordt door de kromming van ruimte-tijd.