Deel III – Fysische Interpretaties

3 Schwarzschild-Metriek

Schwarzschild-Metriek

Het werken met de Einstein-veldvergelijkingen is in het algemeen vrij complex vanwege hun algemene en tensoriële aard. Gelukkig vond Karl Schwarzschild in 1915 een exacte oplossing voor deze vergelijkingen in een specifiek geval: dat van een stationair, sferisch symmetrisch zwaartekrachtsveld in vacuüm. (Zie hoofdstuk 6: Controle of de Schwarzschild Metriek voldoet aan de Einstein Veldvergelijkingen)

Einstein beschouwde in zijn theorie alle mogelijke verdelingen van massa en energie. Schwarzschild beperkte zich daarentegen tot de situatie in het vacuüm, dat wil zeggen: buiten de materie, waar de energie-impulstensor nul is (\(T_{\mu\nu}=0\). ). Hij onderzocht het effect van een centrale, niet-roterende, sferisch symmetrische massa op de omringende ruimte-tijd – bijvoorbeeld de invloed van de zon op passerende planeten of lichtstralen. (Voor een uitgebreider overzicht, zie hoofdstuk 5.11 en Schwarzschild’s: “On the Gravitational Field of a Mass Point According to Einstein’s Theory”.) Schwarzschild beperkte zich tot de situatie waarin de energie-impulstensor nul is \(T_{\mu\nu}=0\).

De door Schwarzschild gevonden metriek luidt:

\[ ds^2 = c^2 d\tau^2 = (1 - \frac{2GM}{c^2 r}) c^2 dt^2 - (1 - \frac{2GM}{c^2 r})^{-1} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta \, d\phi^2 \tag{8} \]

Deze metriek beschrijft de afstand tussen twee gebeurtenissen in een sferisch symmetrisch zwaartekrachtsveld in termen van de tijdcoördinaat \(t\), de radiale afstand \(r\), en de hoeken \(\theta\) en \(\phi\). In een oneindig klein lokaal gebied kunnen we een lokaal inertiaalstelsel construeren waarin de coördinaten \(c dt\), \(dr\), \(d\theta\) en \(d\phi\) zich gedragen als lineaire, orthogonale grootheden. De metrische coëfficiënten zijn in zo'n lokaal vlak constant, maar variëren in het algemeen met \(r\) en \(\theta\).

Voor verdere beschouwingen over deze oplossing zie het volgende hoofdstuk.

Voor de volledige oorspronkelijke afleiding van de Schwarzschild-metriek: zie Schwarzschild, On the Gravitational Field of a Point-Mass, According to Einstein’s Theory, 13 januari 1916, en het overzichtsartikel van Oas.

3.1 Besprekingen over de Schwarzschild-Metriek

3.1.1 Inleiding

De Schwarzschild-metriek is een exacte oplossing van de Einstein-veldvergelijkingen voor het geval van een sferisch symmetrische massa in vacuüm. Karl Schwarzschild publiceerde deze oplossing in 1915, kort na de formulering van de algemene relativiteitstheorie door Albert Einstein. Deze oplossing vormt een van de belangrijkste toepassingen van de theorie en beschrijft hoe massa de structuur van de ruimte-tijd beïnvloedt.

3.1.2 De Schwarzschild-metriek in polaire coördinaten

De Schwarzschild-vergelijking in polaire coördinaten luidt:

\[ ds^2 = c^2 d\tau^2= (1 - \frac{2GM}{c^2 r}) c^2 dt^2 - (1 - \frac{2GM}{c^2 r})^{-1} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta \, d\phi^2 \tag {1} \]

Hierin zijn:

\(G\) de gravitatieconstante,
\(M\) de massa,
\(c\) de lichtsnelheid,
\(t, r, \theta, \phi\) de tijd- en ruimtecoördinaten.

Deze metriek beschrijft de gekromde ruimte-tijd buiten een bolsymmetrische massa, waarbij aangenomen wordt dat er geen andere materie aanwezig is (vacuüm).

3.1.3 Dimensie-analyse

Op het eerste gezicht lijkt het alsof de dimensies van deze vergelijking niet kloppen. In werkelijkheid zijn de coëfficiënten dimensieloos, terwijl de coördinaten een lengte-afmeting hebben (in meter of \(m^2\) voor het kwadraat). De betekenis van formule (1) is dus dat:

\[ ds^2 = \left(1 - \frac{2GM}{c^2 r}\right) d\!\left(c^2 t^2\right) - \left(1 - \frac{2GM}{c^2 r}\right)^{-1} dr^2 - \frac{r^2}{ R_p^2} \, d\!\left(R_p^2 \theta^2\right) - \frac{r^2}{ R_p^2} \sin^2\theta \, d\!\left(R_p^2 \phi^2\right) \]

met \(R_p = 1\) meter. Hiermee wordt duidelijk dat de coördinaten \(r, \theta, \phi\) dimensioneel als lengtes behandeld worden, terwijl de bijhorende coëfficiënten dimensieloos blijven.

Om praktische redenen wordt meestal gewerkt met de oorspronkelijke vorm van vergelijking (1), maar het is belangrijk te beseffen dat \(d\theta\) en \(d\phi\) hier een lengte-dimensie krijgen via vermenigvuldiging met \(R_p\).

3.1.4 Kernpunten en Intuïtie

De Schwarzschild-oplossing werd in 1915 door Karl Schwarzschild gevonden als een exacte oplossing van de Einstein-veldvergelijkingen in het geval van een:

sferisch symmetrisch,
niet-roterend,
statisch massa-object in vacuüm \(T_{\mu\nu}=0\).

De metriek beschrijft hoe ruimte en tijd gekromd worden door een massa \(M\), zoals een ster of planeet, buiten de materie.

De metriek luidt:

\[ ds^2 = c^2 d\tau^2= (1 - \frac{2GM}{c^2 r}) c^2 dt^2 - (1 - \frac{2GM}{c^2 r})^{-1} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta \, d\phi^2 \]

Deze metriek is weergegeven in polaire coördinaten \((t, r, \theta, \phi)\), aangepast aan de sferische symmetrie van het probleem.

De karakteristieke schaal is de Schwarzschild-radius:

\[ r_s = \frac{2GM}{c^2} \]

Voor \(r \to \infty\) benadert de metriek de vlakke Minkowski-metriek, zoals vereist voor asymptotische vlakheid in afwezigheid van massa.

Nabij \(r = r_s\) treden effecten op als tijdsdilatatie, horizonvorming en extreme kromming.

Intuïtief

Stel je voor: een zware ster in de lege ruimte. In plaats van een krachtveld zoals bij Newton, zegt Einstein dat deze massa de ruimte-tijd zelf vervormt.

De Schwarzschild-metriek laat zien hoe sterk die vervorming is op verschillende afstanden:

Tijdsdilatatie: de klok tikt trager dichter bij de massa → bepaald door de factor:
\[ g_{00} =1 - \frac{r_s}{r} \quad \textit{(ook wel } g_{tt}\textit{)} \]
Radiale afstandsvervorming: het meten van een afstand in de \(r\)-richting kost meer “fysieke ruimte” dan je denkt → bepaald door:
\[ g_{11} = \left(1 - \frac{r_s}{r}\right)^{-1} \quad \textit{(ook wel } g_{rr}\textit{)} \]
Hoekcomponenten: \(g_{22}, g_{33}\) blijven klassiek: oppervlak van sferen met straal \(r\).

“De Schwarzschild-oplossing is dus geen abstracte formule, maar een concreet meetbare vervorming van ruimte en tijd – zichtbaar in de loop van klokken en het gedrag van licht en planeten.”

Tabeloverzicht

Grootheid	Betekenis
\(ds^2\)	Lijn-element: meetbare afstand tussen gebeurtenissen
\(g_{00}\)	Bepaalt tijdsdilatatie (hoe tijd verloopt in aanwezigheid van massa)
\(g_{11}\)	Bepaalt vervorming van radiale afstanden
\(r_s = \frac{2GM}{c^2}\)	Schwarzschild-radius (eventuele horizon voor zwart gat)
\(d\Omega^2 = d\theta^2 + \sin^2\theta \, d\phi^2\)	Sferisch oppervlakselement

3.2 Relatie van de Schwarzschild-metriek en Noether’s stelling

3.2.1 Inleiding

Eén van de grote ontdekkingen in de moderne natuurkunde is dat er een diep verband bestaat tussen symmetrieën van de natuurwetten en behoudswetten. Dit verband werd in 1918 wiskundig vastgelegd door Emmy Noether. Haar stelling zegt dat iedere continue symmetrie van een fysisch systeem correspondeert met een behouden grootheid.

De Schwarzschild-oplossing van Einsteins veldvergelijkingen vormt een ideaal laboratorium om dit principe te illustreren. Zij beschrijft de ruimtetijd rond een sferisch symmetrische, niet-roterende massa (zoals een ideaal zwart gat of een niet-roterende ster).

3.2.2 De Schwarzschild-metriek

De ruimtetijd wordt beschreven door de metriek:

\[ ds^2 = (1 - \frac{2GM}{c^2 r}) c^2 dt^2 - (1 - \frac{2GM}{c^2 r})^{-1} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta \, d\phi^2 \]

We zien direct dat deze metriek (d.w.z. de coëfficiënten):

niet expliciet afhangt van \(t\) (tijdsonafhankelijk),
niet expliciet afhangt van \(\phi \) (rotatiesymmetrie),
volledig sferisch symmetrisch is (invariant onder willekeurige ruimtelijke rotaties).

3.2.3 Symmetrieën en Killing-vectoren

In de algemene relativiteit worden symmetrieën van de metriek weergegeven door Killing-vectoren \( \xi^{\mu} \), die voldoen aan de Killing-vergelijking:

\[ \nabla_{\mu}\,\xi_{\nu} \;+\; \nabla_{\nu}\,\xi_{\mu} \;=\; 0 \]

Hierbij betekent \( \nabla_{\mu} \) de covariante afgeleide naar coördinaat \( x^{\mu} \). Deze houdt rekening met de kromming van de ruimtetijd en verschilt van de gewone partiële afgeleide \( \partial_{\mu} \).

Voor een vectorveld geldt bijvoorbeeld:

\[ \nabla_{\mu} V_{\nu}= \partial_{\mu} V_{\nu}+ \Gamma_{\mu\nu}^{\ \ \lambda} \, V_{\lambda} \]

waar \( \Gamma_{\nu\mu}^{\ \ \lambda} \) de Christoffel-symbolen zijn.

De grootheid \( \xi^{\mu} \) stelt een Killing-vectorveld voor: een richting in de ruimtetijd langs welke de metriek niet verandert. Dit is de wiskundige manier om een symmetrie te beschrijven, bijvoorbeeld een tijdstranslatie of een rotatie.

Voor elke Killing-vector geldt langs de geodeet van een testdeeltje:

\[ u^{\mu}\,\xi_{\mu} = \textit{constante} \]

waar \( u^{\mu} \) de viersnelheid van het deeltje is. Dit is de relativistische vorm van Noether’s stelling.

Een lineair verband tussen twee grootheden betekent niet automatisch dat er sprake is van een symmetrie. Een symmetrie houdt in dat de natuurwetten dezelfde vorm behouden wanneer je een bepaalde transformatie uitvoert, zoals een verschuiving in de tijd of een rotatie in de ruimte. Volgens Noether’s stelling hoort bij elk zo'n symmetrie een behouden grootheid. Zo hangt de Schwarzschild‑metriek niet expliciet af van \(t\) , waardoor tijdstranslatie een symmetrie is; dit leidt tot behoud van energie langs de baan van een deeltje. Op dezelfde manier wijst de onafhankelijkheid van \( \phi \) op rotatiesymmetrie, wat resulteert in behoud van impulsmoment. De lineaire relaties waarin deze behouden grootheden vaak verschijnen zijn dus een gevolg van de onderliggende symmetrie — niet de symmetrie zelf.

3.2.4 Toepassing op de Schwarzschild-metriek

a) Tijdstranslatie

De Killing-vector:

\[ \xi^{\mu} = (1,\,0,\,0,\,0) \]

komt overeen met tijdsinvariantie. De bijbehorende constante is de energie per eenheid massa:

\[ E = \left(1 - \frac{2GM}{c^{2} r}\right) c^{2}\, \frac{dt}{d\tau} \]

Hier is \( \frac{dt}{d\tau} \neq 0 \); het deeltje beweegt gewoon in de tijd. Wat behouden blijft, is de combinatie \( g_{00}\,\frac{cdt}{d\tau} \). De behouden grootheid is dus de coëfficiënt van de afgeleide, niet het coördinaat zelf.

b) Rotaties

Er bestaan drie Killing-vectoren die samen de volledige rotatiesymmetrie beschrijven. Een eenvoudige keuze voor de rotatiesymmetrie is de azimutale Killing-vector:

De Killing-vector

\[ \xi^{\mu} = (0,\,0,\,0,\,1) \]

De constante die hieruit volgt is de impulsmomentcomponent:

\[ L = r^{2}\sin^{2}\theta\, \frac{d\phi}{d\tau} \]

Gezamenlijk leiden de drie rotatiesymmetrieën tot behoud van de volledige impulsmomentvector \( (L_x,\,L_y,\,L_z) \). Ook hier is de behouden grootheid de coëfficiënt die de combinatie van afgeleide en metriekcomponent representeert.

3.2.5 Fysische betekenis

Energiebehoud bepaalt hoe een deeltje radiaal invalt of ontsnapt.
Impulsmomentbehoud bepaalt of een baan gesloten is en verklaart fenomenen zoals de periheliumprecessie van Mercurius en de afbuiging van licht.

Zo vertalen symmetrieën van de ruimtetijd zich in meetbare effecten in de astrofysica, waarbij de behoudswetten altijd de coëfficiënten van de afgeleiden langs de geodeet zijn.

3.2.6 Grenzen van Noether in de GR-context

In vlakke ruimte zijn energie en impulsmoment universeel gedefinieerd. In kromme ruimtetijd bestaat niet altijd een wereldwijde tijdsymmetrie.

De Schwarzschild-oplossing is stationair en asymptotisch vlak, waardoor energie- en impulsmomentbehoud geldig en bruikbaar zijn. In dynamische kosmologische ruimtetijden is zo’n globale definitie vaak onmogelijk.

3.2.7 Conclusie

De Schwarzschild-metriek laat zien hoe krachtig Noether’s idee is, ook in de algemene relativiteit. De symmetrieën van de metriek leiden via Killing-vectoren tot behoud van energie en impulsmoment.

Deze behouden grootheden zijn de coëfficiënten van de afgeleiden langs de geodeet, niet de coördinaten zelf. Dit inzicht is essentieel voor het begrijpen van de beweging van deeltjes en licht in zwaartekrachtvelden en vormt de brug tussen de wiskundige structuur van de theorie en de waarneembare fysische fenomenen.

3.3 Fysische interpretatie van de Schwarzschild-metriek

Laten we nu bekijken wat formule (1) fysisch betekent. Stel dat zich in de ruimte een object bevindt met massa \( M \), dat we beschouwen als een puntmassa. In de klassieke Newtoniaanse mechanica veroorzaakt zo’n massa een zwaartekrachtveld – een kracht die werkt op andere massa’s in de buurt.

In de algemene relativiteitstheorie is dit idee fundamenteel anders: volgens Einstein en Schwarzschild genereert de massa \( M \) geen kracht, maar vervormt zij de structuur van de ruimte-tijd. Er is dus geen sprake meer van een kracht in de klassieke zin, maar van een geometrisch effect.

We kiezen een coördinatenstelsel waarin \( M \) zich in het middelpunt bevindt. Wanneer een testdeeltje (met verwaarloosbare massa) zich in rust bevindt ten opzichte van deze massa, ondervindt het in Newtoniaanse zin een zwaartekracht. Laten we dit deeltje los, dan zou het versnellen richting \( M \), net zoals Newton voorspelt.

Toch voelt het deeltje zelf geen kracht. In zijn eigen (meebewegend) referentiekader ervaart het niets bijzonders – het volgt eenvoudig het natuurlijke pad dat de ruimte-tijd zelf voorschrijft. In Einsteins theorie is dit pad geen rechte lijn, maar een geodeet: de kortste of ‘rechtste’ weg in een gekromde ruimte-tijd.

Vector illustratie:

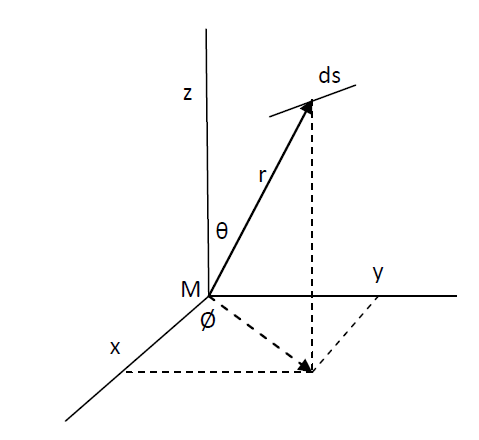
3.3.1 Het gekozen coördinatenstelsel en de lokale structuur van de ruimte

We werken hier met een Euclidisch coördinatenstelsel, dat kan worden opgevat als een Cartesisch systeem (\(t, x, y, z \)) of – zoals in de Schwarzschild-oplossing – een polair systeem (\(t, r, θ, ∅ \)). In het polaire geval hangt het pad dat een deeltje volgt af van alle vier de coördinaten.

De Schwarzschild-metriek schrijft aan elke differentiaal een coëfficiënt toe, die een functie is van \(r\) en \(θ\), maar onafhankelijk is van \(t\) en \(∅\). Dit weerspiegelt de sferische symmetrie rond de massa \(M\): een rotatie om het centrum verandert niets aan de fysische situatie.

Belangrijk om te beseffen is dat deze coördinaten hypothetisch zijn: ze worden gedefinieerd alsof ze zich in een vlakke, niet-gekromde ruimte-tijd bevinden. Schwarzschild vond een expliciete formule die de ruimte-tijd-kromming rond een puntmassa beschrijft. Deze formule relateert het elementaire lijnstuk \(ds\) (de afstand in ruimte-tijd tussen twee naburige gebeurtenissen) aan het gekozen coördinatenstelsel.

Hoewel de ruimte-tijd gekromd is, kunnen we deze lokaal – in een infinitesimaal klein gebied – beschouwen als vlak. Binnen zo’n klein gebied mogen we de coördinaten \(c dt\), \(dr\), \(dθ\), en \(d∅\), behandelen als zijnde onderling loodrecht en rechtlijnig. De coëfficiënten in de metriek kunnen daar als constant worden beschouwd. Verplaatsen we ons naar een andere locatie, dan blijven deze eigenschappen lokaal geldig, maar met gewijzigde coëfficiënten als gevolg van veranderingen in \(r\) en \(θ\).

Door vervolgens over \(ds\) te integreren langs een pad – dat wil zeggen, over alle infinitesimale stapjes samen – verkrijgen we het volledige traject van het deeltje in de gekromde ruimte-tijd.

3.3.2 De Schwarzschild-metriek en de rol van eigen tijd

Zoals eerder besproken, heeft de Schwarzschild-metriek in polaire coördinaten de vorm:

\[ d s^2 = c^2 d\tau^2 = \left(1 - \frac{2GM}{c^2 r}\right)c^2 dt^2 - \left(1 - \frac{2GM}{c^2 r}\right)^{-1} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta\, d\phi^2 \tag{1} \]

Hierin beschrijft \( d s^2 \) het vierkante interval in de ruimte-tijd tussen twee naburige gebeurtenissen.

Voor meer compactheid introduceren we de functie:

\[ \sigma = \sqrt{\,1 - \frac{2GM}{c^2 r}\,} \]

waardoor de metriek elegant herschreven kan worden als:

\[ d s^2 = c^2 d\tau^2 = \sigma^2 c^2 dt^2 - \sigma^{-2} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta\, d\phi^2 \tag{1a} \]

Hierbij is \( d\tau \) de eigen tijd: de tijd die gemeten wordt door een klok die met het object meebeweegt. Dit is de werkelijke tijdsduur die een waarnemer langs zijn eigen wereldlijn ervaart.

De coördinatentijd \( dt \) daarentegen behoort tot een hypothetisch stelsel waarin zich geen massa bevindt - een ideaal “vlak” referentiekader. Strikt genomen is \( dt \) niet direct meetbaar, behalve in de limiet \( r \to \infty \), waar \( \sigma \to 1 \) en de ruimte-tijd vlak wordt.

Lokaal, op een vaste waarde van \( r \), relateert de Schwarzschild-metriek de coördinatentijd en eigen tijd via een eenvoudige relatie:

\[ \Delta t_{\text{coördinaat}} = \sigma\, d t \]

waarin \( \sigma \) afhankelijk is van de positie \( r \).

3.3.3 Afgelegde afstand, snelheid en het verband met de Schwarzschild-metriek

In de Schwarzschild-ruimte-tijd wordt de infinitesimale ruimtelijke afstand Δafstand tussen twee gebeurtenissen gegeven door:

\[ \Delta \textit{afstand} =\sqrt{ \sigma^{-2} dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta\, d\phi^2 }\]

Waarbij, zoals eerder vermeld:

\[ \sigma = \sqrt{\,1 - \tfrac{2GM}{c^2 r}\,} \]

De bijbehorende tijdsduur in coördinatentijd is:

\[ \Delta \textit{tijd} = \sigma\, dt \]

Daaruit volgt voor de (plaatselijke) snelheid \( v \) van een deeltje in het frame:

\[ \frac{v^2}{c^2} = \frac{1}{c^2} \left(\frac{\Delta \textit{afstand}}{\Delta \textit{tijd}} \right)^2 = \frac{\sigma^{-2} dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta\, d\phi^2}{\sigma^2 c^2 dt^2} \]

Hierbij wordt dus rekening gehouden met de kromming van de ruimte-tijd.

Substitueren we deze uitdrukking terug in de compacte vorm van de Schwarzschild-metriek (vergelijking (1a)), dan vinden we:

\[ ds^2 = c^2 d\tau^2 = \sigma^2 c^2 dt^2 - \frac{\sigma^{-2} dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta\, d\phi^2}{\sigma^2 c^2 dt^2}\, \sigma^2 c^2 dt^2 \tag{2} \]

wat vereenvoudigt tot:

\[ c^2 d\tau^2 = \sigma^2 c^2 dt^2 \left[ 1 - \frac{\sigma^{-4}}{c^2}\left(\frac{dr}{dt}\right)^2 - \frac{\sigma^{-2} r^2}{c^2}\left(\frac{d\theta}{dt}\right)^2 - \frac{\sigma^{-2} r^2 \sin^2\theta}{c^2}\left(\frac{d\phi}{dt}\right)^2 \right] \tag{3} \]

of nog compacter geschreven:

\[ c^2 d\tau^2 = \sigma^2 c^2 dt^2 \left(1 - \frac{v^2}{c^2}\right) \]

waarbij:

\[ v^2 = \sigma^{-4}\left(\frac{dr}{dt}\right)^2 + \sigma^{-2} r^2\left(\frac{d\theta}{dt}\right)^2 + \sigma^{-2} r^2 \sin^2\theta\left(\frac{d\phi}{dt}\right)^2 \tag{3a} \]

Deze afleiding laat zien hoe zowel de ruimtelijke als de temporele kromming samen de dynamiek van een bewegend deeltje bepalen.

3.3.4 Verband tussen eigen tijd en coördinatentijd dt

Uit de vorige afleiding (vergelijking (3)) volgt direct de relatie tussen de eigen tijd \( d\tau \) en de coördinatentijd \( dt \):

\[ d\tau = \frac{\sigma}{\gamma} \, dt \]

Waarbij:

\[ \sigma = \sqrt{\,1 - \frac{2GM}{c^2 r}\,}, \qquad \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \tag{4} \]

Hierbij is \(\sigma\) een maat voor de zwaartekrachtsvertraging (door de massa \(M\)) en \(\gamma\) de Lorentzfactor, afkomstig uit de speciale relativiteitstheorie.

Omdat \(\gamma \ge 1\) (immers, \(v \le c\)) en \(\sigma \le 1\) (want \( r \ge 2GM/c^2 \)), volgt hieruit:

\[ d\tau \le dt \tag{5} \]

Dit betekent dat de eigen tijd van het bewegende object altijd langzamer verloopt dan de coördinatentijd in het referentiekader.

Aangezien zowel \(\sigma\) als \(\gamma\) constant zijn tijdens het beschouwde interval (ze zijn slechts functie van \( r \) en \( v \), niet van \( t \)), kunnen we deze relatie eenvoudig integreren:

\[ \tau = \frac{\sigma}{\gamma} \, t \tag{5a} \]

waarbij \(\tau\) de verstreken eigen tijd is en \( t \) de verstreken coördinatentijd.

Hier is dus:

\(t\) is de coördinatentijd van een externe waarnemer (bijvoorbeeld iemand ver weg van het zwaarteveld).
\(\tau\) is de eigentijd van het deeltje zelf.

En:

\(\frac{dt}{d\tau}\) = snelheid waarmee de coördinatentijd verstrijkt ten opzichte van de eigen tijd van het deeltje.
\(\frac{dt}{d\tau}\) is niet een snelheid in meters per seconde zoals \(\frac{dr}{dt}\), maar een relatieve “tijd-snelheid” tussen de coördinatentijd van de waarnemer en de eigentijd van het deeltje.
Het speelt wél dezelfde rol in de Lagrangiaan als een kinetische term: het kwadraat \(dt^2\) komt in de energie-achtige behouden grootheid.

3.3.5 Gedrag van een foton in de Schwarzschild-metriek

Voor een foton geldt dat de eigen tijd \( d\tau \) nul is, omdat een foton altijd met de lichtsnelheid beweegt:

\[ 0 = \sigma^2 c^2 dt^2 - \sigma^{-2} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta \, d\phi^2 \tag{6} \]

Hieruit volgt dat de ruimtelijke afstand die het foton aflegt wordt gegeven door:

\[ \left(\Delta \textit{afstand}\right)^2 = \sigma^{-2} dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta \, d\phi^2 \tag{6b} \]

De effectieve lichtsnelheid \( v \) ten opzichte van het gekozen coördinatensysteem kunnen we nu bepalen:

\[ c^2 = \left(\frac{\Delta \textit{afstand}^2}{\Delta \textit{tijd}} \right)^2 = \frac{\sigma^{-2} dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta \, d\phi^2}{\sigma^2 dt^2} = v^2 \tag{6c} \]

Hierbij is \(\Delta \textit{tijd} = \sigma dt\), zoals eerder besproken.

3.3.6 Interpretatie

In de teller vinden we de 'normale' ruimtelijke afstand die het foton aflegt.
In de noemer zien we dat de *tijd* door een factor \(\sigma\) wordt beïnvloed: de klok op een gegeven locatie tikt trager vanwege de zwaartekrachtsinvloed.

Hieruit blijkt dat, gemeten in de coördinatentijd \( dt \), de lichtsnelheid effectief lager is dan \( c \) in de aanwezigheid van zwaartekracht. In het lokale (meebewegende) frame beweegt het foton natuurlijk nog steeds met de constante snelheid \( c \).

3.3.7 Alternatieve beschrijving van de fotonbeweging

We kunnen de relatie tussen afgelegde afstand en verstreken tijd ook anders herschrijven:

\[ c^2 =\left(\frac{\Delta \textit{afstand}}{\Delta \textit{tijd}} \right)^2= = \frac{\sigma^{-2}\left(\sigma^{-2} dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta \, d\phi^2\right)}{dt^2} \tag{6d} \]

Hierbij merken we op:

De ruimtelijke afstand wordt vergroot met een factor \(\sigma^{-2}\) (aangezien \(\sigma \le 1\)).
Tegelijkertijd blijft de coördinatentijd \( dt \) onveranderd.

3.3.8 Gevolg

Door deze vergrote afstand in de teller, maar een onveranderde tijd in de noemer, lijkt de lichtsnelheid in het coördinatenstelsel kleiner dan de universele lichtsnelheid \( c \).

3.3.9 Samenvattend beeld

Vanuit het standpunt van het 'universele' coördinatenstelsel:

Een foton beweegt langs een kromme in de gekromde ruimte-tijd, en
De effectieve snelheid van het foton tussen twee coördinatiepunten (bijvoorbeeld van A naar B) is kleiner dan \( c \).

In vergelijking:

\[ \sigma^2 c^2 = \frac{\sigma^{-2} dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta\, d\phi^2}{dt^2} \tag{6e} \]

is te zien dat de lichtsnelheid effectief wordt gemodificeerd door de factor \(\sigma^2\).

3.3.10 Gedrag

Dit betekent fysisch dat:

De eigen snelheid van het foton blijft \( c \) langs zijn wereldlijn.
Maar de projectie van zijn beweging op het coördinatenstelsel ziet eruit als een lagere snelheid vanwege de kromming van de ruimte-tijd.

Met andere woorden:

\[ v = \frac{\textit{afstand}}{\textit{t}} = \frac{\textit{afstand}}{\textit{padlengte/c}} =\frac{\textit{afstand}}{\textit{padlengte}}c \]

Omdat de padlengte groter is dan de 'rechte afstand', is \( v < c \) als gemeten in coördinatentijd.

3.3.11 Relatie tussen lokale tijd op Aarde en de universele frametijd

Zoals eerder opgemerkt, is de coördinatentijd \( dt \) een hypothetische tijd, gedefinieerd in een massaloze omgeving of op oneindige afstand \( r = \infty \). Aangezien we onze metingen uitvoeren vanaf de Aarde, moeten we een verband leggen tussen:

de eigen tijd \( d\tau_{\textit{aarde}} \) zoals gemeten door een klok op Aarde, en
de coördinatentijd \( dt \) uit het universele referentiekader.

Zoals eerder afgeleid (zie ook formule (5a)), geldt:

\[ d\tau_{\text{aarde}} = \frac{\sigma_{\textit{aarde}}}{\gamma_{\textit{aarde}}} \, dt \]

Of, omgekeerd:

\[ dt = \frac{\gamma_{\textit{aarde}}}{\sigma_{\textit{aarde}}} \, d\tau_{\textit{aarde}} \]

waarbij:

\(\sigma_{\textit{aarde}} =\sqrt{ 1 - \frac{2GM}{c^2 r_{\textit{aarde}}}}\) de gravitationele tijdsdilatatiefactor is,
\(\gamma_{\textit{aarde}} = \frac{1}{\sqrt{1 - v_{\textit{aarde}}^2 / c^2}}\) de speciale relativistische Lorentzfactor is (wegens de rotatie van de Aarde).

3.3.12 Interpretatie

De tijd op Aarde vertraagt dus relatief gezien vanwege twee effecten:

de zwaartekracht (gravitational time dilation, via \(\sigma\)),
de beweging van de Aarde (speciale relativiteit, via \(\gamma\)).

Voor een waarnemer die meebeweegt met de Aarde blijft zijn eigen *tijd* \( d\tau_{\textit{aarde}} \) natuurlijk normaal verlopen – elke seconde blijft een seconde. Echter, ten opzichte van de universele frametijd \( dt \) lopen de lokale seconden iets trager.

3.3.13 Samenvatting

Op Aarde: eigen klok verloopt normaal (d.w.z. volgens \( d\tau \)).
Ten opzichte van het universele frame: eigen klok loopt vertraagd door zwaartekrachts- en bewegingsinvloeden.

3.3.14 Gedrag van een foton in de Schwarzschild-metriek

Een bijzonder geval treedt op wanneer we een foton beschouwen. Omdat een foton zich altijd met de lichtsnelheid \( c \) voortbeweegt en geen rustmassa heeft, is de eigen tijd \( d\tau \) langs zijn wereldlijn gelijk aan nul:

\[ d\tau = 0 \]

Dit volgt ook direct uit de Schwarzschild-metriek:

\[ 0 = \sigma^2 c^2 dt^2 - \sigma^{-2} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta\, d\phi^2 \tag{6} \]

Hieruit kunnen we afleiden dat de ruimte-afgelegde afstand \( \Delta \textit{afstand} \) is:

\[ (\Delta \textit{afstand})^2 = \sigma^{-2} dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta\, d\phi^2 \tag{6b} \]

en de snelheid van het foton is:

\[ c^2 =\left (\frac{\Delta \textit{afstand}}{\Delta \textit{tijd}}\right)^2 = \frac{\sigma^{-2} dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta\, d\phi^2}{\sigma^2 dt^2} \tag{6c} \]

3.3.15 Opmerking

Hoewel een foton in zijn eigen (niet bestaande) rustframe een "afstand nul" zou hebben, ziet een externe waarnemer wél een afgelegde afstand over een krom pad in de ruimte-tijd.

3.3.16 Speciale gevallen

Radiale beweging van het foton (alleen r-richting, \( d\tau = d\theta = d\phi = 0 \))
Dan vereenvoudigt de vorige vergelijking tot:
\[ c^2 = \sigma^{-4} \left(\frac{dr}{dt}\right)^2 \quad \]

oftewel

Cirkelbeweging in het equatoriale vlak \(\left( \theta = \pi/2 \right)\)
Als het foton zich in een cirkelbaan rond de massa \( M \) bevindt (\( d\tau = dr = d\theta = 0 \)), dan volgt: \[ v = c = \frac{r d\phi}{\sigma dt} \] Hieruit blijkt dat de rotatiesnelheid \( d\phi/dt \) afhankelijk is van de afstand \( r \) en de krommingsfactor \(\sigma\).

3.3.17 Op grote afstand

Als \( r = \infty \), dan geldt \[ \sigma \to 1 \] en dus: \[ d\tau = dt \] De tijd gemeten langs het pad van het foton en de coördinatentijd vallen dan samen – precies zoals we verwachten in een gebied zonder zwaartekracht (vlakke ruimte-tijd).

3.3.18 Samenvattend

Voor een foton geldt altijd \( d\tau = 0 \).
De relatie tussen ruimte en tijd is volledig bepaald door de krommingsfactor \(\sigma\).
In sterk gekromde ruimte-tijd (dicht bij massa) wijkt het gedrag van een foton significant af van wat we intuïtief verwachten in vlakke ruimte-tijd.

In het algemeen is de beweging op oneindige afstand rechtlijnig en uniform, en zo wordt de vergelijking:

\[ ds^2 = c^2 d\tau^2 = c^2 dt^2 - dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta\, d\phi^2 \tag{8} \]

3.3.19 Transformatie naar Cartesiaanse Coördinaten

De oorspronkelijke benadering van Schwarzschild was niet in polaire, maar in Cartesiaanse coördinaten. De transformatie resulteert in:

\[ ds^2 = c^2 d\tau^2 = \sigma^2 c^2 dt^2 - dx^2 - dy^2 - dz^2 - \frac{1-\sigma^2}{\sigma^2 r^2} (x dx + y dy + z dz)^2 \tag{9} \]

Waarbij:

\(\sigma =\sqrt{ 1 - \frac{2GM}{c^2 r}}\)
\( r = \sqrt{x^2 + y^2 + z^2} \) de gebruikelijke radiale afstand is.

3.3.20 Uitleg

De eerste term \( \sigma^2 c^2 dt^2 \) beschrijft de tijdcomponent afhankelijk van de zwaartekracht. De tweede term \( dx^2 + dy^2 + dz^2 \) komt overeen met vlakke ruimte-tijd. De derde term corrigeert voor het feit dat de tijdsvertraging ook ruimte-componenten beïnvloedt, afhankelijk van de richting waarin we bewegen ten opzichte van de massa \( M \).

3.3.21 Opmerking over differentiëren naar t of τ

Tijd \( t \) is de coördinatentijd, gemeten door een waarnemer op oneindige afstand (of in een gebied zonder massa).
Tijd \( \tau \) is de eigentijd, gemeten langs de wereldlijn van het bewegende object.

\[ ds^2 = c^2 d\tau^2 = \sigma^2 c^2 dt^2 - \sigma^{-2} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta\, d\phi^2 \tag{1a} \]

Voor het vlak \( \theta = \pi/2 \) en delen door \( c^2 d\tau^2 \):

\[ 1 = \sigma^2 \left(\frac{dt}{d\tau}\right)^2 - \sigma^{-2} \left(\frac{dr}{c d\tau}\right)^2 - r^2 \left(\frac{d\phi}{c d\tau}\right)^2 \tag{10} \]

of, door om te schrijven met partiële afgeleiden naar \(t\):

\[ 1 = \sigma^2 \left(\frac{dt}{d\tau}\right)^2 - \sigma^{-2} \left(\frac{dr}{c dt} \frac{dt}{d\tau}\right )^2 - r^2 \left(\frac{d\phi}{c dt} \frac{dt}{d\tau}\right)^2 \tag{10} \]

Dan:

\[ 1 = \sigma^2 \left(\frac{dt}{d\tau}\right)^2 \left[ 1 - \frac{1}{\sigma^4} \left(\frac{dr}{cdt}\right)^2 - \frac{r^2}{\sigma^2} \left(\frac{d\phi}{cdt}\right)^2 \right] \tag{11} \]

Hieruit volgt hoe bewegingen (snelheden) en tijdsvertragingen in gekromde ruimte-tijd samenhangen.

3.3.22 Snelheid ten opzichte van lokale en universele tijd

De snelheid ten opzichte van de eigentijd 𝜏 is: \[ v_{\textit{co}}^2 = \frac{\sigma^{-2} dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta\, d\phi^2}{d\tau^2} \]

en de Schwarzschild-metriek kan in termen van \( v_{\textit{co}} \) worden geschreven:

\[ c^2 \, d\tau^2 = \sigma^2 c^2 d t^2 - \frac{\sigma^{-2} dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta\, d\phi^2}{d \tau^2} \, d\tau^2 = \sigma^2 c^2 d t^2 - v_{co}^2 d\tau^2 \]

Of herschreven:

\[ c^2 d\tau^2 + v_{co}^2 d\tau^2 = \sigma^2 c^2 d t^2 \]

Benadering voor kleine snelheden \( (v_{co} \ll c) \) via een Taylor-reeks:

\[ d\tau^2 =\frac{ \sigma^2 }{ 1 +\left( \dfrac{v_{co}}{c}\right)^2} d t^2 \, \approx \, \sigma^2 \left( 1 - \dfrac{v_{co}^2}{c^2} \right) d t^2 \]

\[ d\tau \approx \sigma \sqrt{1 - \frac{v_{\textit{co}}^2}{c^2}} dt \quad\Rightarrow\quad d\tau =\frac {\sigma}{ \gamma_{\textit{co}}} dt \]

Met \( \gamma_{co} = \dfrac{1}{\sqrt{1 - \dfrac{v_{co}^2}{c^2}}} \).

3.3.23 Samenvatting

Schwarzschild werkte oorspronkelijk in Cartesiaanse coördinaten.
De Schwarzschild-metriek kan worden herleid naar zowel bol- als Cartesiaanse vorm.
Bij interpretaties van beweging is het essentieel om onderscheid te maken tussen coördinatentijd \( t \) en eigentijd \( \tau \).
Voor kleine snelheden is de invloed van ruimte-tijdkromming op de tijd klein, maar meetbaar.

Over het algemeen speelt een traject zich af in één vlak. Dan kan het polaire systeem zo gekozen worden dat het evenaarsvlak samenvalt met het trajectvlak (\( \theta = \pi/2 \)). Als het traject een cirkel is (\( r \) constant), dan is \( dr = 0 \) en wordt:

\[ c^2 d\tau^2 = \sigma^2 c^2 dt^2 - r^2 d\phi^2 \]

Hierna volgen een aanvullende overpeinzingen:

3.3.24 Aanvulling 1: Interpretatie van ds als Lijnsegment in de Ruimte-tijd

Misschien is het nuttig om ds te beschouwen als een oneindig klein lijnsegment in de ruimte-tijd, waarvan de lengte in meters kan worden gemeten door de reistijd van een foton over dat segment te vermenigvuldigen met de lichtsnelheid c. Het lijnsegment ds bevindt zich in de oorsprong van zijn eigen meebewegend referentiekader. Binnen dat kader is tijd de enige fysische grootheid die direct kan worden gemeten. De afstand wordt gemeten via de reistijd van het foton.

Dus:

\[ ds = c\,d\tau \]

waarbij \( d\tau \) de eigen tijd is die op een meebewegende klok wordt geregistreerd.

Nu introduceren we een tweede referentiekader, bijvoorbeeld het Schwarzschild-kader, waarin zich een centrale massa M bevindt. In dit kader kunnen we de afstand tussen het lijnsegment en de oorsprong bepalen door gebruik te maken van externe meetinstrumenten (zoals lasers, staven, enzovoort).

Belangrijk:
De tijdsbepaling in dit externe kader is indirect: ze is afhankelijk van de relatie die wordt gegeven door de Schwarzschild-metriek, en kan niet direct worden gemeten met een klok ter plaatse.

Volgens de Schwarzschild-metriek geldt:

\( c^{2}d\tau^{2} = \left(c\Delta T\right)^{2} - \left( \Delta X \right)^{2} \)

\( \left(c\Delta T\right)^{2} = \left(1 - \dfrac{2GM}{c^{2}r}\right)c^{2}dt^{2} =c^{2}d\tau^{2} - \left( \Delta X \right)^{2} \)

waarbij \( \Delta X \) de ruimtelijke component is:

\( \left( \Delta X \right)^{2} = \dfrac{1}{1 - \dfrac{2GM}{c^{2}r}}\,dr^{2} + r^{2}d\theta^{2} + r^{2}\sin^{2}\theta\,d\phi^{2} \)

Hieruit volgt:

\( c^{2}dt^{2} = \dfrac{\left(c\Delta T\right)^{2}}{1 - \dfrac{2GM}{c^{2}r}} \)

De relatie tussen de theoretische tijd dt en de eigen tijd \( d\tau \) kan alleen via deze formule worden bepaald.

3.3.25 Aanvulling 2: Wereldlijn van een Deeltje in een Meebewegend Referentiekader

Beschouwen we een deeltje in een meebewegend (lokaal) referentiekader, dan is het deeltje in rust ten opzichte van dat kader. Het enige pad dat het deeltje volgt in de ruimte-tijd is langs zijn eigen τ-as: de eigen tijd.

We kunnen echter de beweging van het deeltje beschrijven ten opzichte van een extern (mogelijk bewegend) referentiekader. In dat geval drukken we de positie van het deeltje uit in coördinaten \((t, x, y, z)\) van dat andere kader.

De wereldlijn van het deeltje — het pad dat het deeltje volgt door de ruimte-tijd — is dan volledig een functie van \(\tau\):

\[ t(\tau), x(\tau), y(\tau), z(\tau) \]

De vier coördinaten zijn dus functies van de eigen tijd \(\tau\).

3.3.26 Voorbeeld: Tijdsverschil tussen de Polen en de Evenaar

We berekenen het tijdsverschil aan het aardoppervlak tussen de tijd bij de polen en aan de evenaar, veroorzaakt door relativistische effecten.

Uitgaande van de Schwarzschild-metriek:

\[ c^2 d\tau^2 = \sigma^2 c^2 dt^2 - \sigma^{-2} dr^2 - r^2 d\theta^2 - r^2 \sin^2\theta\, d\phi^2 \]

3.3.27 Bij de Polen

Aan de polen geldt:

\(dr = 0\) (geen radiale beweging),
\(θ = 0\),
\(dθ = 0\),
\(sin θ = 0\).

Dan wordt de Schwarzschild-metriek: \[ c^2 d\tau^2_{\textit{polen}} = \sigma^2 c^2 dt^2 \] waaruit volgt: \[ d\tau_{\textit{polen}} = \sigma dt \]

3.3.28 Bij de Evenaar

Aan de evenaar geldt:

\(dr = 0\),
\(θ = π/2\),
\(dθ = 0\),
\(sinθ = 1\)

Dan wordt de metriek: \[ c^2 d\tau^2_{\textit{evenaar}} = \sigma^2 c^2 dt^2-r^2 d\phi^2 \] waarbij \(dφ\) de draaiing om de rotatie-as van de Aarde beschrijft.

We herschrijven dit: \[ c^2 d\tau^2_{\textit{evenaar}} = c^2 d\tau^2_{polen}-r^2 d\phi^2 \] Of: \[ c^2 d\tau^2_{\textit{evenaar}} = c^2 d\tau^2_{polen} \left(1-\frac{r^2}{c^2} \left(\frac{d\phi}{d\tau_{polen}}\right)^2\right) \] De draaisnelheid \(v_{evenaar}\) aan de evenaar is: \[ v_{evenaar}=r\frac{d\phi}{d\tau_{polen}} \]

Dus: \[ c^2 d\tau^2_{\textit{evenaar}} = c^2 d\tau^2_{polen} \left(1-\frac{v^2_{evenaar}}{c^2} \right) \] en \[ d\tau_{evenaar}=d\tau_{polen}\sqrt{1-\frac{v^2_{evenaar}}{c^2}} \]

Voor kleine snelheden \(v ≪ c\) kunnen we dit benaderen via een Taylor-reeks: \[ d\tau_{evenaar}\approx d\tau_{polen}\left(1-\frac{1}{2}\frac{v^2_{evenaar}}{c^2}\right) \]

3.3.29 Praktische Berekening

De rotatiesnelheid aan de evenaar is ongeveer:
\[≈ 1672 km/h \quad of \quad 465 m/s\] Dit resulteert in: \[ \frac{v^2_{evenaar}}{c^2} \approx 2.4 \cdot 10^{-12} \] Daarmee geldt: \[ d\tau_{evenaar}= d\tau_{polen} \sqrt {1-2.4 \cdot 10^{-12}} \]

3.3.30 Interpretatie

Een klok aan de evenaar tikt iets trager dan een klok aan de polen. Over een periode van 100 jaar zou het verschil oplopen tot ongeveer:

100 jaar * 1.2·10⁻¹² ≈ 3,75 milliseconden

3.3.31 Conclusie

Een persoon die 100 jaar op de Noordpool heeft geleefd, zou (theoretisch) 3,75 milliseconden ouder zijn dan iemand die aan de evenaar verbleef, als alle andere omstandigheden gelijk zijn gebleven.

3.3.32 Aanvulling 3: De Schwarzschild-coëfficiënt en de Ontsnappingssnelheid

Laten we speciale aandacht besteden aan de factor: \[ 1-\frac{2GM}{c^2r} \]

Deze uitdrukking doet denken aan de bekende formule voor de ontsnappingssnelheid, die bepaalt welke minimale snelheid een massa moet hebben om een andere massa (bijvoorbeeld de aarde) te kunnen verlaten.

3.3.33 Berekening van de Minimale Ontsnappingssnelheid

Beschouwen we een massa m die wordt weggeschoten van een object met massa M (bijvoorbeeld de aarde), dan is:

De kinetische energie van m: \[E_{\text{kin}} = \frac{1}{2} m v^2\]
De gravitatiekracht die m ondervindt: \[F = \frac{G M m}{r^2}\]

waarbij r de afstand tot het centrum van massa M is.

Het werk dat verricht moet worden om de massa m van r naar oneindig te brengen(waarbij de zwaartekrachtsinvloed nul is), is: \[ W = \int_r^\infty F \, ds =\int_r^\infty \frac{G M m}{s^2} \, ds =-G\frac{M m}{s}\int_r^\infty \, ds \] \[ = G M m \left(\frac{1}{r}-\frac{1}{\infty}\right)=G\frac{M m}{r} \]

Om te kunnen ontsnappen, moet de kinetische energie gelijk zijn aan dit werk: \[ \frac{1}{2} m v^2 = \frac{G M m}{r} \] Waaruit volgt: \[ v^2 = \frac{2 G M}{r} \] \[ v = \sqrt{\frac{2 G M}{r}} \] Of omgekeerd:

\[ r = \frac{2 G M}{v^2} \]

3.3.34 De Maximale Snelheid: Licht

De maximale snelheid die een object kan bereiken is de lichtsnelheid c. Indien v = c, dan wordt de bijbehorende afstand: \[ r = \frac{2 G M}{c^2} \] Dit is de zogeheten Schwarzschild-radius: \[ r = R_s = \frac{2 G M}{c^2} \] Wanneer een object zich binnen deze straal bevindt, is het onmogelijk om eraan te ontsnappen - zelfs licht kan niet ontsnappen. In dat geval spreken we van een zwart gat.

3.3.35 Verband met de Schwarzschild-metriek

In de Schwarzschild-metriek verschijnt deze straal in de factor:

\[ 1 - \frac{2 G M}{c^2 r} \]

Normaal gesproken ligt deze factor tussen 1 en 0:

Voor grote afstanden \(r → ∞\) nadert de factor 1.
Nabij de Schwarzschild-radius \(r = R_s\) wordt de factor 0.

Wanneer \(1 - 2GM/(c² r) = 0\), bevindt het object zich precies op de Schwarzschild-radius, oftewel op de gebeurtenishorizon van een zwart gat.

3.3.36 Opmerking

Als \(r\) kleiner wordt dan \(R_s\), zou de factor negatief worden. Wat dit fysiek betekent, vereist diepere analyse binnen de relativistische theorie van zwarte gaten, en gaat verder dan wat hier wordt behandeld.

3.3.37 Kernpunten en Intuïtie

In de algemene relativiteit vervangt geometrie de kracht: massa kromt ruimte-tijd in plaats van een krachtveld te genereren.
De Schwarzschild-metriek beschrijft deze kromming rondom een sferisch symmetrische massa en geldt buiten de massa, waar \(T_{\mu \nu}=0\).
Een testdeeltje dat beweegt in dit veld voelt geen kracht, maar volgt een geodeet - het 'rechtste' pad in gekromde ruimte-tijd.
De metriek in bolcoördinaten: \[ ds^2 = c^2 d\tau^2 = \sigma^2 c^2 dt^2 − \sigma^{-2} dr^2 − r^2 d\theta^2 − r^2 sin^2 \theta \, d\phi^2 \] met \[ \sigma = 1 - \frac{2GM}{c^2 r}\]
De coördinatentijd dt geldt in het asymptotisch vlakke (hypothetische) kader op \(r → ∞\); de eigen tijd \(dτ\) wordt gemeten door een klok die meebeweegt met het object.

Intuïtief: Einstein stelt: een massa beïnvloedt de meetstructuur van ruimte en tijd zelf. Een vrij vallend object beweegt niet “door een kracht”, maar volgt het pad dat de geometrie van de ruimte-tijd oplegt - vergelijkbaar met een kiezelsteen die rolt in een krom oppervlak.

De tijd verloopt langzamer dichter bij een massa (via \(σ < 1)\).
De ruimte is uitgerekt in de radiale richting.
Voor een bewegend object relateert de metriek dτ aan dt én zijn snelheid ν:
\(dτ = σ\, γ\, dt,\) met \(\, γ = 1 / \sqrt{1 - v²/c²}\)

Tabel: Begrippen en fysische grootheden uit de Schwarzschild-metriek

Grootheid	Fysische interpretatie
σ = 1 - 2GM/(c² r)	Gravitationele tijdsdilatatiefactor
dτ	Eigen tijd: gemeten door een lokale klok
dt	Coördinatentijd: gemeten in asymptotisch vlak referentiekader
v	Lokale snelheid, afgeleid uit ruimtelijke coördinaten en dt
ds² = c² dτ²	Vierdimensionaal interval (invariant): tijds- en ruimte-element
R_s = 2GM/c²	Schwarzschild-radius: waar σ = 0, gebeurtenishorizon

3.3.38 Specifieke gevallen en effecten

Fotonen:
- Volgen een traject met \(dτ = 0\): ze ervaren geen eigen tijd.
- De effectieve lichtsnelheid in coördinatentijd is kleiner dan \(c\) (maar lokaal blijft \(v = c)\).
Object in rust bij massa:
- Tijdsdilatatie via \(dτ = \frac{σ}{γ} dt\): hoe kleiner \(r\), hoe langzamer de klok.
Object in beweging (bijv. cirkelbaan):
- Zowel gravitationele als kinematische tijdsdilatatie spelen een rol.
- Vergelijking voor snelheid in Schwarzschild-coördinaten:
  \[ v² = σ^{-4} (\frac {dr}{dt})^2 + σ^{-2} r^2 (\frac {dθ}{dt})^2 + σ^{-2} r^2 sin^2θ (\frac {d\phi}{dt})^2 \tag{3a}\]

3.3.39 Toepassing: Tijd op Aarde vs. Tijd op oneindige afstand

Tijd op Aarde vertraagt ten opzichte van de universele coördinatentijd, zowel door:
- zwaartekracht (via \( σ \) ),
- rotatie van de Aarde (via \( γ \) ).
Resultaat: over 100 jaar is een klok aan de polen ≈ 3,75 ms voor op een klok aan de evenaar (bij benadering).

3.3.40 Zwarte gaten en ontsnappingssnelheid

Uit Newtons mechanica volgt:
\( ν_{\text{ontsnapping}} = \sqrt{\frac{2 G M}{r}} ⟹ R_s = \frac{2 G M}{c^2} \)
Bij \( r = R_{s} \) wordt \( σ → 0 \) (gebeurtenishorizon): niets kan ontsnappen.
De Schwarzschild-metriek bevat deze grens expliciet.

3.3.41 Slotinzicht

De Schwarzschild-metriek levert direct meetbare voorspellingen:

Tijdsdilatatie (o.a. GPS-correcties)
Lichtafbuiging (zoals gemeten tijdens zonsverduisteringen)
Periheliumprecessie van Mercurius
Voorwaarden voor het ontstaan van zwarte gaten

De Schwarzschild-metriek is dus geen abstract wiskundig object, maar een fysische machine die ons vertelt hoe klokken lopen, hoe licht buigt, en hoe massa’s bewegen - puur op basis van de geometrie van ruimte en tijd.

3.4 Experimenten: Bevestiging van de Algemene Relativiteit

De algemene relativiteitstheorie is niet alleen een elegante wiskundige theorie, maar wordt ook krachtig ondersteund door experimenten en waarnemingen. Veel van deze experimenten maken gebruik van de Schwarzschild-oplossing als basis voor hun theoretische voorspellingen. De volgende experimenten worden in dit werk besproken:

Hafele-Keating-experiment (1971) (zie hoofdstuk 4.1)
- Beschrijving: Atoomklokken werden in vliegtuigen rond de aarde gevlogen, zowel oostwaarts als westwaarts, en vergeleken met klokken op de grond.
- Resultaat: De gemeten tijdsverschillen kwamen exact overeen met de voorspellingen van de algemene relativiteit (zwaartekrachts-tijdsdilatatie én bewegings-tijdsdilatatie).
- Relatie tot Schwarzschild-metriek: De tijdsdilatatie door zwaartekracht wordt direct uit de Schwarzschild-oplossing afgeleid.

Beweging van deeltjes in een zwaartekrachtveld (zie hoofdstuk 4.2)
- Beschrijving: De banen van satellieten, planeten en andere objecten worden nauwkeurig gevolgd.
- Resultaat: De waargenomen banen komen overeen met de voorspellingen uit de Schwarzschild-geometrie, inclusief kleine afwijkingen van de klassieke (Newtonse) voorspellingen.

Afbuiging van licht nabij massa’s (zie hoofdstuk 4.3)
- Beschrijving: Tijdens zonsverduisteringen werd gemeten hoe het licht van sterren wordt afgebogen door de zwaartekracht van de zon.
- Resultaat: De gemeten afbuiging (door Eddington in 1919 en vele latere experimenten) komt exact overeen met de waarde voorspeld door de Schwarzschild-metriek.
- Fysisch belang: Bewijst dat licht zelf wordt beïnvloed door de kromming van ruimte-tijd.

Precessie van de periheliën (Mercurius) (zie hoofdstuk 4.4)
- Beschrijving: De baan van Mercurius draait langzaam rond de zon; deze precessie kan niet volledig door Newtonse zwaartekracht verklaard worden.
- Resultaat: De resterende precessie wordt exact verklaard door de Schwarzschild-oplossing.
- Historisch belang: Dit was een van de eerste grote successen van de algemene relativiteit.

Shapiro-tijdvertraging (zie hoofdstuk 4.5)
- Beschrijving: Radiogolven die langs de zon reizen, doen er langer over dan verwacht in vlakke ruimte-tijd.
- Resultaat: De extra tijdsvertraging komt overeen met de voorspelling van de Schwarzschild-metriek.
- Toepassing: Wordt gebruikt in radar- en communicatiesatellieten.

Baan van een kogel in een sterk zwaartekrachtsveld (zie hoofdstuk 4.8)
- Beschrijving: Simulaties en metingen van objecten die zich met hoge snelheid in de buurt van massieve objecten bewegen.
- Resultaat: De banen wijken af van Newtonse voorspellingen, maar komen overeen met de Schwarzschild-voorspellingen.

Conclusie

In al deze experimenten zijn de resultaten in uitstekende overeenstemming met de voorspellingen van de algemene relativiteitstheorie, zoals afgeleid uit de Schwarzschild-metriek. Dit vormt een krachtige bevestiging van de juistheid van Einsteins theorie.

Kernpunt

De algemene relativiteitstheorie is niet alleen een wiskundig elegante theorie, maar wordt ook experimenteel bevestigd tot op hoge precisie. De Schwarzschild-metriek vormt daarbij de sleutel tot het begrijpen van de meeste klassieke tests van de zwaartekracht.