Appendix 9 — Speciale Relativiteitstheorie
In de Speciale Relativiteitstheorie beschouwde Einstein alleen coördinatenstelsels die uniform bewogen, dus met constante snelheid ten opzichte van elkaar. De invloed van massa’s, en dus zwaartekracht, werd niet meegenomen.
De aannames waarop de Speciale Relativiteitstheorie (SR) is gebaseerd, zijn:
- De maximaal mogelijke snelheid, in elk coördinatenstelsel, is de lichtsnelheid \(c = 299\,792\,458\ \text{m/s}\).
- De natuurwetten zijn geldig in elk uniform bewegend coördinatenstelsel.
In de benadering van Newton waren de tijdsintervallen gelijk in het “ruststelsel” en in het bewegende stelsel. Echter, via de Speciale Relativiteitstheorie werd aangetoond dat:
- de tijdsintervallen in een bewegend stelsel kleiner zijn dan in een ruststelsel (tijdsvertraging),
- de lengte van een object afneemt in de bewegingsrichting (lengtecontractie).
Beide effecten volgen uit de waarneming dat de lichtsnelheid in vacuüm altijd hetzelfde is in elk stelsel, ongeacht de snelheid van het stelsel.
In dit hoofdstuk vatten we een aantal punten samen die vaak worden gebruikt in de SR en die relevant zijn voor toepassingen in de algemene relativiteitstheorie (GR).
We beginnen met het vaststellen van de relatie tussen twee coördinatenstelsels die met een constante snelheid ten opzichte van elkaar bewegen. Deze relatie staat bekend als de Lorentztransformatie.
Appendix 9.1 — Eenvoudige Afleiding van de Lorentztransformatie
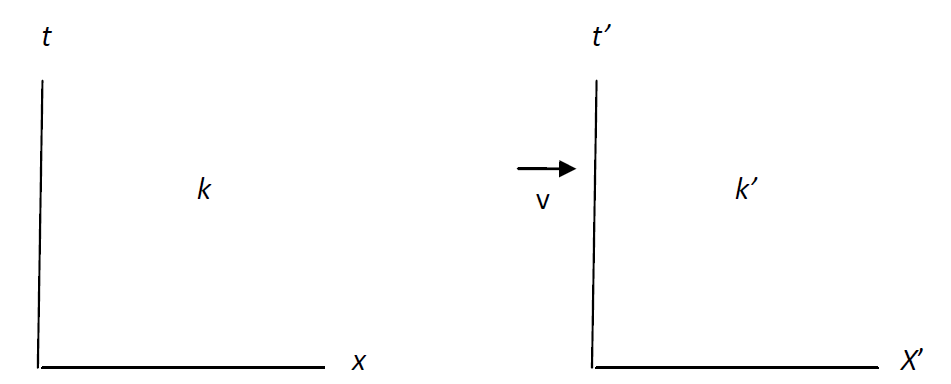
Coördinaat systeem k’ beweegt uniform met een snelheid v ten
opzichte van coördinaat systeem k.
We nemen twee coördinatensystemen waarvan de oorsprongen zich met een constante snelheid \(v\) ten opzichte van elkaar bewegen, respectievelijk in de \(x\)- en \(x'\)-richting.
Hoewel de coördinatenstelsels vierdimensionaal zijn \((t, x, y, z)\), worden alleen de \(t\)- en \(x\)-assen getekend omwille van de eenvoud, omdat er geen beweging is in de \(y\)- en \(z\)-richtingen.
Een lichtsignaal dat op tijd \(t = t' = 0\) wordt uitgezonden in de positieve \(x\)-richting, voldoet in het stelsel \(k\) aan:
\[ x = ct \quad\Rightarrow\quad x - ct = 0. \tag{1} \]
Aangezien hetzelfde lichtsignaal zich ook met snelheid \(c\) voortplant in het stelsel \(k'\), geldt daar:
\[ x' = ct' \quad\Rightarrow\quad x' - ct' = 0. \tag{2} \]
Alle ruimte‑tijdpunten (gebeurtenissen) die aan (1) voldoen, moeten ook aan (2) voldoen. Dit is gegarandeerd wanneer:
\[ x' - ct' = \lambda (x - ct), \tag{3} \]
waarbij \(\lambda\) een constante is. Als \(x - ct = 0\), dan volgt automatisch \(x' - ct' = 0\), ongeacht de waarde van \(\lambda\).
Lichtsignaal in de negatieve richting
Voor een lichtsignaal dat langs de negatieve \(x\)-as beweegt, geldt in \(k\):
\[ x + ct = 0, \]
en in \(k'\):
\[ x' + ct' = 0. \]
Daarom moet gelden:
\[ x' + ct' = \mu (x + ct), \tag{4} \]
met \(\mu\) een tweede constante.
Lineaire combinatie van de twee voorwaarden
Door (3) en (4) op te tellen en af te trekken, en de constanten
\[ a = \frac{\lambda + \mu}{2}, \qquad b = \frac{\lambda - \mu}{2}, \]
in te voeren, verkrijgen we:
\[ x' = a x - b c t, \qquad ct' = a ct - b x. \tag{5} \]
Dit is de algemene lineaire vorm van de Lorentztransformatie, waarbij de constanten \(a\) en \(b\) nog moeten worden bepaald.
Bepaling van de constante verhouding \(b/a\)
Voor de oorsprong van \(k'\) geldt permanent:
\[ x' = 0. \]
Invullen in de eerste vergelijking van (5) geeft:
\[ 0 = a x - b c t \quad\Rightarrow\quad x = \frac{b c}{a}\, t. \]
De oorsprong van \(k'\) beweegt dus in \(k\) met snelheid:
\[ v = \frac{b c}{a}. \tag{6} \]
Deze waarde \(v\) is de relatieve snelheid van de twee stelsels. Dezelfde waarde volgt wanneer men de snelheid van een willekeurig ander punt van \(k'\) ten opzichte van \(k\) berekent, of omgekeerd.
Het relativiteitsprincipe leert ons dat — zoals beoordeeld vanuit \(k\) — de lengte van een meetlat die in rust is ten opzichte van \(k'\), precies gelijk moet zijn aan de lengte van een meetlat die in rust is ten opzichte van \(k\), zoals beoordeeld vanuit \(k'\).
Om te zien hoe de punten op de \(x'\)-as er vanuit \(k\) uitzien, maken we een momentopname van \(k'\) vanuit \(k\). Dit betekent dat we een vaste waarde van \(t\) kiezen, bijvoorbeeld:
\[ t = 0. \]
Voor deze waarde volgt uit de eerste vergelijking van (5):
\[ x' = a x. \]
Twee punten op de \(x'\)-as die in \(k'\) gescheiden zijn door een afstand \(x' = L\), zijn in onze momentopname gescheiden door:
\[ \Delta x = \frac{L}{a}. \tag{7} \]
Momentopname vanuit \(k'\): \(t' = 0\)
Als de momentopname wordt gemaakt vanuit \(k'\), dus bij \(t' = 0\), dan volgt uit de tweede vergelijking van (5):
\[ 0 = a c t - b x \quad\Rightarrow\quad t = \frac{b}{a c} x. \]
Invullen in de eerste vergelijking van (5):
\[ x' = a x - b c t = a x - b c \left(\frac{b}{a c} x\right) = a x \left(1 - \frac{b^{2}}{a^{2}}\right). \]
Uit vergelijking (6): \[ \frac{b}{a} = \frac{v}{c}, \] dus:
\[ x' = a \left(1 - \frac{v^{2}}{c^{2}}\right) x. \tag{7a} \]
Daarom worden twee punten op de \(x\)-as, gescheiden door afstand \(L\) in \(k\), in de momentopname vanuit \(k'\) weergegeven door:
\[ \Delta x' = a\left(1 - \frac{v^{2}}{c^{2}}\right) L. \tag{7b} \]
Gelijkheid van de twee momentopnamen
Volgens het relativiteitsprincipe moeten beide momentopnamen identiek zijn:
\[ \Delta x = \Delta x'. \]
Dus volgens de vergelijkingen (7) en (7b):
\[ \frac{L}{a} = a\left(1 - \frac{v^{2}}{c^{2}}\right) L. \]
Na vereenvoudigen:
\[ \frac{1}{a} = a\left(1 - \frac{v^{2}}{c^{2}}\right) \quad\Rightarrow\quad a^{2} = \frac{1}{1 - v^{2}/c^{2}}. \tag{7c} \]
Daarmee:
\[ a = \gamma = \frac{1}{\sqrt{1 - v^{2}/c^{2}}}, \qquad b = \gamma \frac{v}{c}. \]
De Lorentztransformatie
Door deze waarden van \(a\) en \(b\) in (5) te substitueren, verkrijgen we:
\[ x' = a x - b c t = \gamma x - \gamma v t = \gamma (x - v t). \]
En:
\[ ct' = a c t - b x = \gamma c t - \gamma \frac{v}{c} x = \gamma\left(ct - \frac{v}{c} x\right). \]
Dus de volledige Lorentztransformatie luidt:
\[ \boxed{ \begin{aligned} x' &= \gamma (x - vt), \\ t' &= \gamma\left(t - \frac{v}{c^{2}}x\right). \end{aligned} } \]
Lorentztransformatie voor gebeurtenissen op de x-as
Uit de eerdere afleiding volgt de Lorentztransformatie:
\[ x' = \frac{x - vt}{\sqrt{1 - v^{2}/c^{2}}}, \qquad t' = \frac{t - \frac{v}{c^{2}}x}{\sqrt{1 - v^{2}/c^{2}}}. \tag{8} \]
Deze transformatie voldoet aan de invariantie van het ruimte‑tijd‑interval:
\[ x'^{2} - c^{2}t'^{2} = x^{2} - c^{2}t^{2}. \tag{8a} \]
Uitbreiding naar gebeurtenissen buiten de x-as
Voor beweging uitsluitend langs de x‑as blijven de transformaties voor de andere coördinaten onveranderd:
\[ y' = y, \qquad z' = z. \tag{9} \]
Met (8) en (9) voldoen we aan het postulaat dat de lichtsnelheid in vacuüm in elk inertiaalstelsel dezelfde waarde heeft.
Controle met een lichtsignaal
Een lichtsignaal dat vanuit de oorsprong van \(k\) wordt uitgezonden op tijd \(t = 0\), voldoet aan:
\[ r = \sqrt{x^{2} + y^{2} + z^{2}} = ct. \]
Kwadrateren geeft:
\[ x^{2} + y^{2} + z^{2} - c^{2}t^{2} = 0. \tag{10} \]
Volgens het relativiteitsprincipe moet hetzelfde signaal in \(k'\) voldoen aan:
\[ x'^{2} + y'^{2} + z'^{2} - c^{2}t'^{2} = 0. \tag{10a} \]
Om (10a) een gevolg te laten zijn van (10), moet gelden:
\[ x'^{2} + y'^{2} + z'^{2} - c^{2}t'^{2} = \zeta\, \left( x^{2} + y^{2} + z^{2} - c^{2}t^{2} \right). \tag{11} \]
Maar voor punten op de x‑as geldt reeds (8a), dus:
\[ \zeta = 1. \]
Daarmee is aangetoond dat de Lorentztransformatie (8)–(9) de lichtsnelheid invariant laat.
Algemene vorm van de Lorentztransformatie
De Lorentztransformatie zoals hierboven afgeleid geldt voor het geval waarin:
- de assen van \(k\) en \(k'\) parallel zijn,
- de relatieve snelheid \(v\) langs de x‑as ligt.
Maar dit is geen beperking. In het algemeen kunnen we elke Lorentztransformatie construeren uit:
- een Lorentztransformatie in de specifieke zin (translatie langs één as),
- gevolgd door een zuiver ruimtelijke rotatie van het coördinatenstelsel.
Dit komt overeen met het vervangen van het rechthoekige coördinatenstelsel door een nieuw stelsel waarvan de assen in andere richtingen wijzen.
Zo verkrijgen we de volledige Lorentzgroep, bestaande uit alle combinaties van translaties en rotaties.
De gegeneraliseerde Lorentztransformatie
Wiskundig kunnen we de gegeneraliseerde Lorentztransformatie als volgt karakteriseren: zij drukt \(x', y', z', t'\) uit in termen van lineaire homogene functies van \(x, y, z, t\), zodanig dat de relatie
\[ x'^2 + y'^2 + z'^2 - c^2 t'^2 = x^2 + y^2 + z^2 - c^2 t^2 \tag{11a} \]
identiek wordt voldaan. Dat wil zeggen: wanneer we de uitdrukkingen voor \(x', y', z', t'\) in termen van \(x, y, z, t\) substitueren in de linkerkant, dan wordt deze identiek aan de rechterkant.
Gebruik van een imaginaire tijdscoördinaat
We kunnen de Lorentztransformatie nog eenvoudiger karakteriseren door de imaginaire grootheid \(i\) te introduceren, waarbij \(i\) staat voor \(\sqrt{-1}\). Definieer:
\[ x_1 = x,\qquad x_2 = y,\qquad x_3 = z,\qquad x_4 = i\,ct. \]
En analoog voor het geaccentueerde systeem \(k'\). Dan wordt de transformatievoorwaarde:
\[ x_1'^2 + x_2'^2 + x_3'^2 + x_4'^2 = x_1^2 + x_2^2 + x_3^2 + x_4^2. \tag{12} \]
Met deze keuze van “coördinaten” wordt vergelijking (11a) omgezet in (12).
We zien dat de imaginaire tijdscoördinaat \(x_4\) in de transformatievoorwaarde op exact dezelfde manier voorkomt als de ruimtelijke coördinaten \(x_1, x_2, x_3\). Dit weerspiegelt het relativistische inzicht dat tijd en ruimte op gelijke voet staan in de natuurwetten.
Minkowski‑ruimte
Een vierdimensionaal continuüm beschreven door de coördinaten \((x_1, x_2, x_3, x_4)\) werd door Minkowski de wereld genoemd. Een puntgebeurtenis heet een wereldpunt.
De vierdimensionale “wereld” vertoont een sterke analogie met de driedimensionale Euclidische ruimte. In de Euclidische meetkunde geldt voor een rotatie:
\[ x_1'^2 + x_2'^2 + x_3'^2 = x_1^2 + x_2^2 + x_3^2. \]
De analogie met (12) is compleet: de Lorentztransformatie komt overeen met een “rotatie” in de vierdimensionale Minkowski‑ruimte, waarbij de tijdscoördinaat imaginaire component draagt.
Appendix 9.2 — Alternatieve afleiding van tijddilatatie en lengtecontractie
We leiden nu de relatie af tussen de tijd \(t\) in ons coördinatenstelsel en de tijd \(t'\) in een systeem dat met snelheid \(v\) beweegt.
We nemen de oorsprongen van beide stelsels samen op tijdstip:
\[ t = t' = 0. \]
Zoals Einstein stelde, is de snelheid van het licht in elk inertiaalstelsel dezelfde. Daarom moet een lichtsignaal dat in ons stelsel met snelheid \(c\) beweegt, ook in het bewegende stelsel met snelheid \(c\) bewegen.
Tijddilatatie via een lichtflits loodrecht op de bewegingsrichting
We beschouwen een persoon in een snel bewegend object, bijvoorbeeld een raket, die een lichtflits aanzet in een richting loodrecht op de bewegingsrichting van de raket.
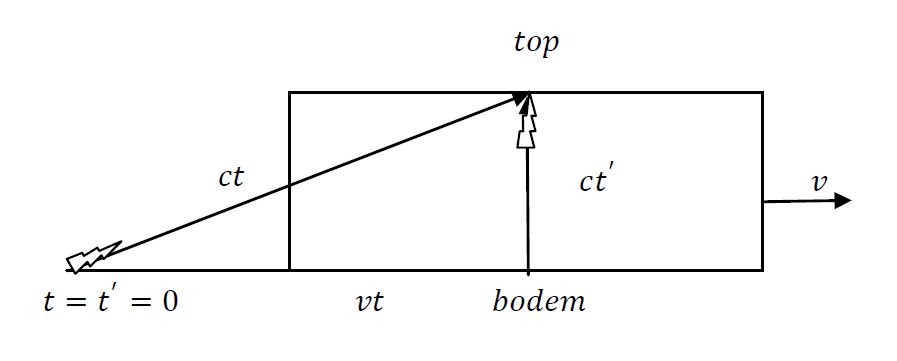
De tijd in ons (stilstaand) stelsel wordt aangeduid met \(t\), en de tijd in de bewegende raket met \(t'\).
In de raket gaat de lichtflits recht omhoog. De afgelegde verticale afstand in de raket is:
\[ c t'. \]
Vanuit ons stilstaande stelsel beweegt de raket horizontaal met snelheid \(v\). Daarom beweegt de lichtflits — terwijl hij omhoog gaat — ook horizontaal mee.
We vergelijken nu de afgelegde afstanden in beide stelsels.
In ons stelsel legt de lichtflits een schuine afstand af:
\[ c t. \]
De horizontale verplaatsing van de raket (en dus van de lichtflits) is:
\[ v t. \]
Daarom geldt volgens de stelling van Pythagoras:
\[ c^{2} t^{2} = c^{2} t'^{2} + v^{2} t^{2}. \]
Herschrijven geeft:
\[ c^{2} t^{2} - v^{2} t^{2} = c^{2} t'^{2}, \] \[ t^{2}(c^{2} - v^{2}) = c^{2} t'^{2}, \] \[ t^{2}\left(1 - \frac{v^{2}}{c^{2}}\right) = t'^{2}. \]
Dus:
\[ \boxed{ t' = t \sqrt{1 - \frac{v^{2}}{c^{2}}} } \]
Dit toont aan dat de tijd \(t'\) in de raket altijd korter is dan de tijd \(t\) in ons stilstaande stelsel: tijddilatatie.
Lengtecontractie via een lichtflits in de bewegingsrichting
Nu sturen we een lichtflits in de horizontale richting, dus in de richting van de beweging.
Omdat de raket horizontaal beweegt, is er geen verticale beweging. De verticale richting wordt dus niet beïnvloed door de snelheid.
De horizontale richting wél, omdat de lichtflits en de raket beide horizontaal bewegen.
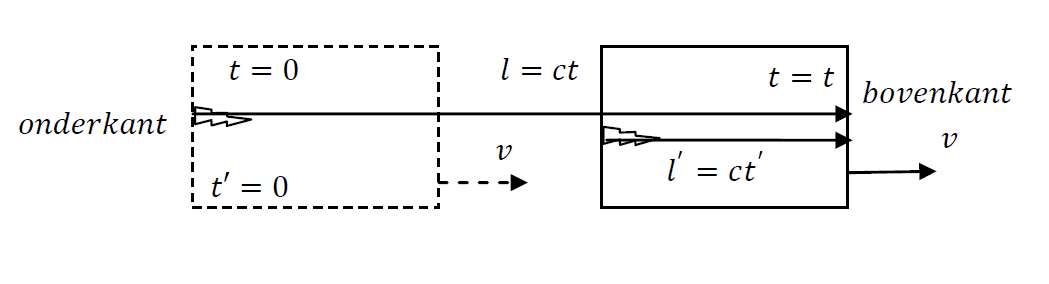
We beschouwen de afstand die de flits aflegt vanaf het moment dat deze begint aan de linkerkant van de raket tot het moment dat deze de rechterkant bereikt.
In ons stelsel is de afgelegde afstand:
\[ \ell = c t. \]
In de raket is de afgelegde afstand:
\[ \ell' = c t'. \]
Omdat we hierboven hebben gevonden dat:
\[ t' = t \sqrt{1 - \frac{v^{2}}{c^{2}}}, \]
volgt:
\[ \ell' = c t' = c t \sqrt{1 - \frac{v^{2}}{c^{2}}} = \ell \sqrt{1 - \frac{v^{2}}{c^{2}}}. \]
Dus:
\[ \boxed{ \ell' = \ell \sqrt{1 - \frac{v^{2}}{c^{2}}} } \]
Dit toont aan dat de lengte van een object dat met snelheid \(v\) beweegt, korter wordt in de bewegingsrichting: lengtecontractie.
Conclusie van tijddilatatie en lengtecontractie
De lichtsnelheid in ons stelsel is gelijk aan de lichtsnelheid in de raket, zoals gezien vanuit ons gezichtspunt:
\[ c = \frac{\ell}{t} = \frac{\ell'}{t'}. \]
Uit het eerste deel weten we dat:
\[ t' = t \sqrt{1 - \frac{v^{2}}{c^{2}}}. \]
Daarom:
\[ \frac{\ell}{t} = \frac{\ell'}{t'} = \frac{\ell'}{t \sqrt{1 - v^{2}/c^{2}}}, \]
dus:
\[ \ell = \frac{\ell'}{\sqrt{1 - v^{2}/c^{2}}}, \qquad \ell' = \ell \sqrt{1 - \frac{v^{2}}{c^{2}}}. \]
De resulterende relaties zijn:
\[ \boxed{ t' = t \sqrt{1 - \frac{v^{2}}{c^{2}}} } \qquad\text{(tijddilatatie)} \]
\[ \boxed{ \ell' = \ell \sqrt{1 - \frac{v^{2}}{c^{2}}} } \qquad\text{(lengtecontractie)} \]
Dus, gezien vanuit ons referentiekader, is de tijd in het raketstelsel korter dan onze tijd en is de lengte van de raket korter in de bewegingsrichting.
Appendix 9.3 Symmetrie in de beïnvloeding van ruimtetijd door Lorentz-transformaties
Hoewel de \(y\)- en \(z\)-coördinaten zelf numeriek constant blijven, verandert de tijdscomponent \(t\) wél onder de Lorentz-transformatie. Hierdoor verlopen processen die zich afspelen in de \(y\)- of \(z\)-richting volgens een veranderde tijdsbasis.
\[ x'=\gamma(x-vt) \] \[ t'=\gamma\left(t-\frac{v}{c^2}x\right) \] \[ y'=y \] \[ z'=z \]Een klok die zich op een vaste \(y\)-positie bevindt, tikt langzamer voor een waarnemer in rust, precies zoals een klok op een vaste \(x\)-positie dat doet. Hetzelfde geldt voor gebeurtenissen in het \(y\)-\(t\)- of \(z\)-\(t\)-vlak: hoewel de ruimtelijke component niet verandert, is de tijdscomponent wel getransformeerd.
Omgekeerd geldt voor de vlakken \(y\)-\(x\) en \(z\)-\(x\): hoewel de \(y\)- en \(z\)-coördinaten constant blijven, verandert de \(x\)-coördinaat door de Lorentz-transformatie. Ook deze vlakken worden dus beïnvloed, al is dat in veel toepassingen minder direct zichtbaar.
Deze overweging leidt tot een belangrijk inzicht: de invloed van een Lorentz-transformatie is niet beperkt tot het vlak waarin de snelheid zich manifesteert (het \(x\)-\(t\)-vlak), maar werkt structureel door in de gehele ruimtetijd. Elk vlak waarin een van de getransformeerde coördinaten \(x\) of \(t\) voorkomt, wordt mede bepaald door deze transformatie.
Vanuit dit perspectief ontstaat een vorm van structurele symmetrie: ook al veranderen \(y\) en \(z\) zelf niet, toch zijn processen in die richtingen afhankelijk van een getransformeerde tijd- of ruimtecomponent. De volledige ruimtetijd wordt hergestructureerd, en daarmee alle fysische beschrijvingen binnen dat stelsel.
Appendix 9.4 Goniometrische Hulpmiddelen
Omdat goniometrische formules vaak worden gebruikt in de speciale relativiteitstheorie, geven we een kort overzicht van een aantal ervan en hoe ze gemakkelijk kunnen worden afgeleid.
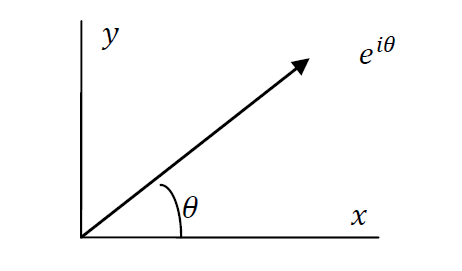
Per definitie:
\[ e^{i\theta} = \cos\theta + i\sin\theta \tag{1} \]
Waarbij: \[ i=\sqrt{-1} \]
Onderbouwing van deze vergelijking:
We beschouwen eerst een functie:
\[ F(x) = e^{\alpha x}. \]
De afgeleide hiervan is:
\[ \frac{dF(x)}{dx} = \alpha F(x). \]
Dus de afgeleide van een exponentiële functie is een factor \(\alpha\) maal die functie.
Complexe goniometrische functie
Beschouw nu de functie:
\[ F(x) = \cos(\alpha x) + i\sin(\alpha x). \]
De afgeleide hiervan is:
\[ \frac{d}{dx}\left[\cos(\alpha x) + i\sin(\alpha x)\right] = -\alpha\sin(\alpha x) + i\alpha\cos(\alpha x) = i\alpha\left[\cos(\alpha x) + i\sin(\alpha x)\right]. \]
Dus:
\[ \frac{dF(x)}{dx} = i\alpha F(x). \]
Hieruit volgt dat:
\[ F(x) = e^{i\alpha x} = \cos(\alpha x) + i\sin(\alpha x). \]
Voor \(\alpha = 1\) krijgen we de bekende Euler‑vergelijking:
\[ \boxed{ e^{i\theta} = \cos\theta + i\sin\theta } \tag{1} \]
Afgeleide goniometrische formules
Uit (1) volgt direct:
\[ e^{-i\theta} = \cos\theta - i\sin\theta. \tag{2} \]
Door (1) en (2) op te tellen:
\[ \cos\theta = \frac{e^{i\theta} + e^{-i\theta}}{2}. \]
Door (1) en (2) van elkaar af te trekken:
\[ \sin\theta = \frac{e^{i\theta} - e^{-i\theta}}{2i}. \]
Verder:
\[ e^{i\theta} \cdot e^{-i\theta} = e^{i\theta - i\theta} = e^{0} = 1, \]
en:
\[ (\cos\theta + i\sin\theta)(\cos\theta - i\sin\theta) = \cos^{2}\theta + \sin^{2}\theta = 1. \]
Hyperbolische functies
We definiëren:
\[ \cosh x = \frac{e^{x} + e^{-x}}{2}, \qquad \sinh x = \frac{e^{x} - e^{-x}}{2}. \]
Hieruit volgt:
\[ \cosh(x) = \cosh(-x), \qquad \sinh(x) = -\sinh(-x). \]
Verder geldt:
\[ \cosh(ix) = \cos x, \qquad \sinh(ix) = i\sin x. \]
Dus:
\[ \boxed{ \cosh(ix) = \cos x,\qquad \sinh(ix) = i\sin x. } \]
Deze relaties vormen de basis voor het gebruik van hyperbolische functies in de speciale relativiteitstheorie, met name bij het beschrijven van Lorentz‑boosts via rapiditeit.
Appendix 9.5 — Optelling van snelheden
We beschouwen twee coördinatensystemen \(A\) en \(B\) die met een constante snelheid \(v\) ten opzichte van elkaar bewegen. De assen zijn zo gekozen dat de relatieve beweging langs de \(x\)-assen plaatsvindt.
In systeem \(A\) beweegt een object met snelheid \(V'_x, V'_y, V'_z\). We willen nu de snelheid van dit object bepalen ten opzichte van systeem \(B\).
Volgens Newton zou de snelheid in de \(x\)-richting eenvoudig zijn: \[ V_x = V'_x + v. \] Maar volgens de speciale relativiteitstheorie is dit niet correct.
Lorentz-transformatie
We beginnen met de Lorentz-transformaties:
\[ ct' = \gamma(ct - \beta x), \tag{1} \] \[ x' = \gamma(x - \beta ct), \tag{2} \] \[ y' = y,\qquad z' = z, \]
waar: \[ \gamma = \frac{1}{\sqrt{1 - v^{2}/c^{2}}},\qquad \beta = \frac{v}{c}. \]
De inverse transformatie luidt:
\[ ct = \gamma(ct' + \beta x'), \tag{1a} \] \[ x = \gamma(x' + \beta ct'), \tag{2a} \] \[ y = y',\qquad z = z'. \]
Snelheid in de \(x'\)-richting
Neem de afgeleide van (2):
\[ V'_x = \frac{dx'}{dt'} = \gamma\frac{dx}{dt}\frac{dt}{dt'} - \beta c \frac{dt}{dt'} = \gamma(V_x - \beta c)\frac{dt}{dt'}. \tag{3} \]
Neem nu de afgeleide van (1):
\[ c = \gamma\left(c\frac{dt}{dt'} - \beta \frac{dx}{dt}\frac{dt}{dt'}\right) = \gamma\left(c - \beta V_x\right)\frac{dt}{dt'}. \]
Dus:
\[ \frac{dt}{dt'} = \frac{1}{\gamma\left(1 - \beta\frac{V_x}{c}\right)}. \tag{4} \]
Vul (4) in in (3):
\[ V'_x = \gamma(V_x - \beta c) \cdot \frac{1}{\gamma\left(1 - \beta\frac{V_x}{c}\right)} = \frac{V_x - v}{1 - \frac{v V_x}{c^{2}}}. \tag{5} \]
Dit is de relativistische snelheidsoptelling in de \(x\)-richting.
Resultaat
\[ \boxed{ V'_x = \frac{V_x - v}{1 - \frac{v V_x}{c^{2}}} } \]
Dit vervangt de Newtoniaanse optelling \(V'_x = V_x - v\).
De snelheden in de andere richtingen worden:
\[ V'_y = \frac{V_y}{\gamma\left(1 - \frac{v V_x}{c^{2}}\right)}, \qquad V'_z = \frac{V_z}{\gamma\left(1 - \frac{v V_x}{c^{2}}\right)}. \tag{6} \]
Deze formules tonen dat snelheden niet eenvoudig optellen in de relativiteitstheorie, maar worden beïnvloed door zowel de Lorentz-factor als de projectie van de snelheid op de bewegingsrichting.
Uit vergelijking (5) hadden we reeds:
\[ V'_x = \frac{\gamma(V_x - \beta c)}{\gamma\left(1 - \beta \frac{V_x}{c}\right)} = \frac{V_x - \beta c}{1 - \beta \frac{V_x}{c}} = \frac{V_x - v}{1 - \frac{v V_x}{c^{2}}}. \tag{5} \]
Snelheid in de \(y'\)-richting
\[ V'_y = \frac{\partial y'}{\partial t'} = \frac{\partial y}{\partial t'} = \frac{\partial y}{\partial t}\frac{dt}{dt'} = V_y \frac{dt}{dt'}. \]
Uit vergelijking (4):
\[ \frac{dt}{dt'} = \gamma\left(1 - \beta\frac{V_x}{c}\right), \]
dus:
\[ V'_y = \frac{V_y}{\gamma\left(1 - \beta\frac{V_x}{c}\right)}. \tag{6} \]
Snelheid in de \(z'\)-richting
Op identieke wijze volgt:
\[ V'_z = \frac{V_z}{\gamma\left(1 - \beta\frac{V_x}{c}\right)}. \tag{7} \]
Interpretatie van vergelijking (4)
Uit (4):
\[ \frac{dt}{dt'} = \frac{1}{\gamma\left(1 - \beta\frac{V_x}{c}\right)} = \frac{1 - v^{2}/c^{2}}{1 - \frac{v V_x}{c^{2}}}. \]
In het speciale geval waarin \(V'_x = 0\), geldt \(V_x = v\). Dan wordt:
\[ \frac{dt}{dt'} = \frac{1 - v^{2}/c^{2}}{1 - v^{2}/c^{2}} = \frac{1}{1 - v^{2}/c^{2}} = \gamma^{2}. \]
Dus:
\[ dt' = \sqrt{1 - \frac{v^{2}}{c^{2}}}\, dt, \]
en dus:
\[ dt' \ll dt. \]
Dit is opnieuw de tijddilatatie.
Terug naar het algemene geval
Uit (5):
\[ V'_x = \frac{V_x - v}{1 - \frac{v V_x}{c^{2}}}. \]
Oplossen naar \(V_x\) geeft:
\[ V_x = \frac{V'_x + v}{1 + \frac{v V'_x}{c^{2}}}. \]
Dit is de inverse relativistische snelheidsoptelling.
In compacte vorm:
\[ \boxed{ V_x = \frac{V'_x + v}{1 + \beta \frac{V'_x}{c}} } \tag{5a} \]
Voor de andere componenten volgt op analoge wijze:
\[ V_y = \frac{V'_y}{\gamma\left(1 + \beta\frac{V'_x}{c}\right)}, \tag{6a} \]
en:
\[ V_z = \frac{V'_z}{\gamma\left(1 + \beta\frac{V'_x}{c}\right)}. \tag{7a} \]
Samenvatting
De relativistische snelheidsoptelling luidt:
\[ \boxed{ V'_x = \frac{V_x - v}{1 - \frac{v V_x}{c^{2}}} } \]
\[ \boxed{ V'_y = \frac{V_y}{\gamma\left(1 - \frac{v V_x}{c^{2}}\right)} } \]
\[ \boxed{ V'_z = \frac{V_z}{\gamma\left(1 - \frac{v V_x}{c^{2}}\right)} } \]
en de inverse transformatie:
\[ \boxed{ V_x = \frac{V'_x + v}{1 + \frac{v V'_x}{c^{2}}} } \]
\[ \boxed{ V_y = \frac{V'_y}{\gamma\left(1 + \frac{v V'_x}{c^{2}}\right)} } \]
\[ \boxed{ V_z = \frac{V'_z}{\gamma\left(1 + \frac{v V'_x}{c^{2}}\right)} } \]
Voor de \(z\)-component volgt op dezelfde manier:
\[ V'_z = \frac{V_z}{\gamma\left(1 + \beta \frac{V'_x}{c}\right)}. \tag{7a} \]
Volgens Newton zouden we in de \(x\)-richting eenvoudig een toegevoegde snelheid hebben:
\[ V_x = V'_x + v. \]
Maar volgens de speciale relativiteitstheorie wordt dit gecorrigeerd tot:
\[ V_x = \frac{V'_x + v}{1 + \frac{v V'_x}{c^{2}}}. \]
In het algemeen, wanneer de term \(\frac{v V'_x}{c^{2}}\) zeer klein is, kan men het relativistische resultaat benaderen door het Newton-resultaat:
\[ V_x \approx V'_x + v. \]
Appendix 9.6 Botsingen
Stel een perfect elastische botsing voor tussen twee identieke deeltjes; een elastische botsing is een botsing zonder verlies van kinetische energie. De beginsnelheden van de deeltjes zijn respectievelijk \(\vec{u_1}\) en \(\vec{u_2}\) en na de botsing \(\vec{v_1}\) en \(\vec{v_2}\). Vanwege de impulsbehoud geldt: \[ m_{1u}u_1+m_{2u}u_2=m_{1v}v_1+m_{2v}v_2 \] Hier zijn \(m_{1u}\) en \(m_{2u}\) de massa’s vóór de botsing en \(m_{1v}\) en \(m_{2v}\) de massa’s na de botsing.
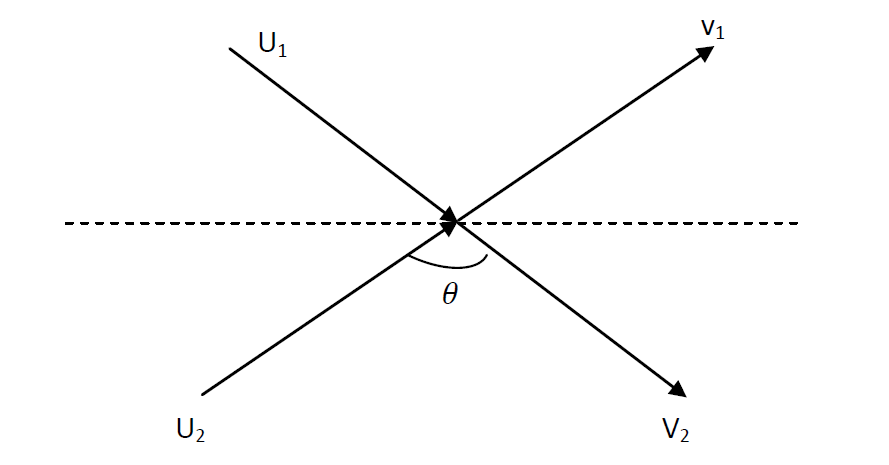
Eerst beschouwen we de botsing vanuit een coördinatensysteem dat beweegt met deeltje één. Dan beweegt deeltje 1 naar boven met snelheid \(w_1\) en naar beneden met \(w_2\). Deze snelheden zijn gelijk, maar tegengesteld. Deeltje 2 heeft snelheid 𝑉 met een x-component u en een y-component v.
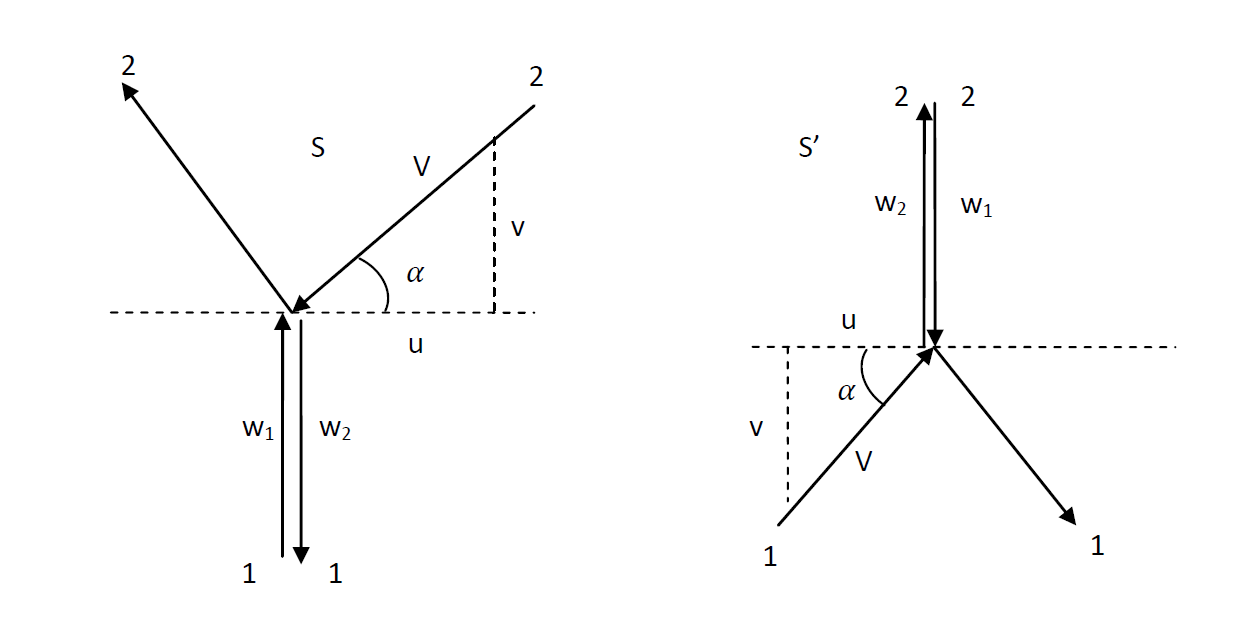
Relatie tussen de y‑componenten van de impuls
We willen nu de relatie vinden tussen de y‑componenten van de impuls van de deeltjes 1 en 2 in systeem \(S\), dus tussen \(w\) en \(v\).
In het vorige hoofdstuk vonden we de relatie:
\[ V'_y = \frac{V_y}{\gamma\left(1 - \beta \frac{V_x}{c}\right)}. \]
Aangezien in dit geval: \[ V_y = w,\qquad V_x = 0, \] krijgen we:
\[ v = \frac{w}{\gamma} \]
Vanwege de symmetrie is \(w\) de snelheid van deeltje 1 in systeem \(S\) en de snelheid van deeltje 2 in systeem \(S'\). Omgekeerd is \(v\) de y‑component van deeltje 2 in \(S\) en van deeltje 1 in \(S'\).
Totale snelheid
De totale snelheid van het bewegende deeltje in \(S\) en in \(S'\) is dezelfde:
\[ V = \sqrt{v^{2} + u^{2}}. \]
Impulsbehoud in de y‑richting
Het impulsbehoud in de y‑richting geeft:
\[ m_w w - m_V v = -m_w w + m_V v. \]
Hieruit volgt:
\[ m_w w = m_V v. \]
Dus:
\[ \frac{m_V}{m_w} = \frac{w}{v} = \frac{w}{w/\gamma} = \gamma. \tag{1} \]
Dit resultaat laat zien dat de Lorentz‑factor \(\gamma\) rechtstreeks voortkomt uit impulsbehoud in een botsing die symmetrisch wordt bekeken vanuit twee inertiaalstelsels.
Limiet van kleine snelheden
Stel nu dat de snelheid \(w\) zeer klein is. In deze limiet geldt:
\[ \lim_{w \to 0} v = 0, \qquad \lim_{w \to 0} V = u. \]
In dat geval kunnen de relativistische effecten worden verwaarloosd en kan de klassieke uitdrukking voor impuls worden teruggevonden.
Omdat: \[ \lim_{w \to 0} m_w = m, \] vullen we dit in in vergelijking (1):
\[ \lim_{w \to 0} m_V = \gamma m = \frac{m}{\sqrt{1 - \frac{u^{2}}{c^{2}}}}. \]
Vanwege impulsbehoud moet de definitie van impuls worden aangepast. De relativistische impuls wordt daarom:
\[ \boxed{ \vec{p} = \gamma m \vec{v} } \]
Appendix 9.7— De Energie van een Bewegend Object
Met het gedachte-experiment toonde Einstein aan dat energie en massa equivalent zijn via de relatie \(𝐸=𝑚𝑐^2\). We hebben laten zien dat voor een object dat met een snelheid beweegt, de impuls moet worden aangepast aan de relativistische beschrijving: \[ \vec{p}=\gamma m \vec{v} \] Dus kan worden gesteld dat de energie van een object gelijk is aan: \[ E=\gamma m c^2 \] Dus: \[ E=\frac{mc^2}{\sqrt{1-\frac{u^2}{c^2}}} \] Met de Taylorreeksontwikkeling: \[ E=\gamma m c^2 \approx mc^2\left(1+\frac{v^2}{2c^2}-\frac{3v^4}{8c^4}\text{.....} \right) \] Als 𝑣 veel kleiner is dan 𝑐, kunnen de derde en volgende termen binnen de haakjes worden verwaarloosd. Dit leidt tot: \[ E\approx mc^2+\frac{1}{2}mv^2 \] Dus dit is de kinetische energie \(\frac{1}{2}mv^2\) plus een constante \(𝑚𝑐^2\).
Appendix 9.8— Energie‑Impulsvector
Zoals gevonden door Minkowski, is het interval in de ruimtetijd:
\[ c^{2} d\tau^{2} = c^{2} dt^{2} - dx^{2} - dy^{2} - dz^{2}. \tag{1} \]
We schrijven dit als:
\[ c^{2} d\tau^{2} = c^{2} dt^{2} \left( 1 - \frac{dx^{2} + dy^{2} + dz^{2}}{c^{2} dt^{2}} \right) = c^2dt^{2}\left(1 - \frac{v^{2}}{c^{2}}\right). \]
Aangezien: \[ \gamma = \frac{1}{\sqrt{1 - v^{2}/c^{2}}}, \] volgt:
\[ 1 - \frac{v^{2}}{c^{2}} = \frac{1}{\gamma^{2}}, \qquad d\tau^{2} = \frac{dt^{2}}{\gamma^{2}}, \qquad \gamma = \frac{dt}{d\tau}. \]
Afleiding van de energie‑impulsrelatie
Begin opnieuw bij (1):
\[ c^{2} = c^{2}\left(\frac{dt}{d\tau}\right)^{2} - \left(\frac{dx}{dt}\right)^{2}\left(\frac{dt}{d\tau}\right)^{2} - \left(\frac{dy}{dt}\right)^{2}\left(\frac{dt}{d\tau}\right)^{2} - \left(\frac{dz}{dt}\right)^{2}\left(\frac{dt}{d\tau}\right)^{2} \]
Vermenigvuldig met de rustmassa \(m_{0}^{2}\):
\[ m_{0}^{2} c^{2} = m_{0}^{2} c^{2}\left(\frac{dt}{d\tau}\right)^{2} - m_{0}^{2}\left(\frac{dx}{dt}\right)^{2}\left(\frac{dt}{d\tau}\right)^{2} - m_{0}^{2}\left(\frac{dy}{dt}\right)^{2}\left(\frac{dt}{d\tau}\right)^{2} - m_{0}^{2}\left(\frac{dz}{dt}\right)^{2}\left(\frac{dt}{d\tau}\right)^{2} \]
Omdat: \[ \frac{dt}{d\tau} = \gamma, \] krijgen we:
\[ m_{0}^{2} c^{2} = \gamma^{2} m_{0}^{2} c^{2} - \gamma^{2} m_{0}^{2} v_x^{2} - \gamma^{2} m_{0}^{2} v_y^{2} - \gamma^{2} m_{0}^{2} v_z^{2}. \]
Definieer nu de vier‑impuls:
\[ p_{0} = \frac{E}{c}, \qquad p_{1} = p_x, \qquad p_{2} = p_y, \qquad p_{3} = p_z, \]
met: \[ p_i = \gamma m_0 v_i. \]
Dan wordt de Minkowski‑norm:
\[ p_{tau}^{2} = \left(\frac{E}{c}\right)^{2} - p_x^{2} - p_y^{2} - p_z^{2} = m_{0}^{2} c^{2}. \]
Of compacter:
\[ E^{2} - c^{2} |\vec{p}|^{2} = m_{0}^{2} c^{4}. \]
Dus:
\[ \boxed{ E^{2} = m_{0}^{2} c^{4} + c^{2} p^{2} } \]
en voor positieve energie:
\[ \boxed{ E = +\sqrt{m_{0}^{2} c^{4} + c^{2} p^{2}}. } \]
We hadden gevonden dat: \[ p = \gamma m_0 v = \frac{m_0 v}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}, \] waarbij \(m_0\) de rustmassa is (de massa bij snelheid nul).
Uit de relatie: \[ E = \frac{m_0 c^{2}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \] volgt:
\[ E^{2} = \frac{m_0^{2} c^{4}}{1 - \frac{v^{2}}{c^{2}}}. \]
Na verder delen:
\[ E^{2} = m_0^{2} c^{4} + \frac{m_0^{2} c^{4} \frac{v^{2}}{c^{2}}}{1 - \frac{v^{2}}{c^{2}}} = m_0^{2} c^{4} + \frac{m_0^{2} v^{2} c^{2}}{1 - \frac{v^{2}}{c^{2}}}. \]
Maar: \[ p = \frac{m_0 v}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \quad\Rightarrow\quad p^{2} = \frac{m_0^{2} v^{2}}{1 - \frac{v^{2}}{c^{2}}}. \]
Dus: \[ E^{2} = m_0^{2} c^{4} + p^{2} c^{2}. \]
Of zoals men gebruikelijk schrijft:
\[ \boxed{ E^{2} = p^{2} c^{2} + m_{0}^{2} c^{4} } \tag{2} \]
waarbij dus: \[ p = \frac{m_0 v}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}. \]
Appendix 9.8.1 Alternatieve afleiding van de Energie-Impuls-Massa relatie
We hadden: \[ p=mv \] \[ p=\gamma m_0 v=\gamma m_0 c^2 \frac{v}{c^2} \] \[ pc=\gamma m_0 c^2\frac{v}{c}=\beta \gamma m_0 c^2 \]
Hier is:
\[ \gamma=\frac{1}{\sqrt{1-\beta^2}} \quad \text{en} \quad \beta=\frac{v}{c} \]Nu, met gebruik van bovenstaande, bekijken we wat er gebeurt:
\[ \left( pc \right)^2+\left(m_0c^2 \right)^2=\left(\beta \gamma m_0 c^2 \right)^2+\left(m_0c^2 \right)^2 \] \[ \left( pc \right)^2+\left(m_0c^2 \right)^2=\left(m_0 c^2 \right)^2\left(\beta^2\gamma^2+1\right)^2 \] \[ \left( pc \right)^2+\left(m_0c^2 \right)^2=\left(m_0 c^2 \right)^2\left(1+\beta^2 \frac{1}{1-\beta^2}\right)^2 \] \[ \left( pc \right)^2+\left(m_0c^2 \right)^2 =\left(m_0 c^2 \right)^2\left(\frac{1-\beta^2+\beta^2}{1-\beta^2}\right)^2 =\left(m_0 c^2 \right)^2\left(1+\beta^2 \frac{1}{1-\beta^2}\right)^2=\left(m_0 c^2\right)^2 \gamma^2 \] \[ \left( pc \right)^2+\left(m_0c^2 \right)^2=\left(m_0 c^2\right)^2 \gamma^2 =\left(\gamma m_0 c^2\right)^2=E^2 \]Dus:
\[ \boxed{ E^{2} = p^{2} c^{2} + m_{0}^{2} c^{4} } \]Appendix 9.8.2 — Klassiek Bewijs van Energieconservatie
De totale mechanische energie van een deeltje is de som van de kinetische energie \(K\) en de potentiële energie \(U\):
\[ E = \frac{1}{2} m v^{2} + U(x). \]Neem de tijdsafgeleide (ééndimensionale beweging):
\[ \frac{dE}{dt} = m v \frac{dv}{dt} + \frac{dU}{dx}\frac{dx}{dt} = m v a + v \frac{dU}{dx}. \]De kracht die hoort bij een potentiële energie \(U(x)\) is:
\[ F = -\frac{dU}{dx}. \]Daarmee wordt:
\[ \frac{dE}{dt} = v\left( m a + \frac{dU}{dx} \right) = v\left( m a - F \right). \]Volgens de tweede wet van Newton geldt:
\[ F = m a. \]Dus:
\[ \frac{dE}{dt} = 0. \]Daarmee volgt:
\[ \boxed{E = \text{constant}} \]De totale mechanische energie is dus geconserveerd.
Appendix 9.9 Afleiding van \(E=mc^2\)
Einsteins gedachte-experiment met de lichtpuls in een doos
Einstein vond de vergelijking \(E = mc^{2}\) door middel van een elegant gedachte-experiment. Beschouw een stationaire doos die vrij in de ruimte zweeft, zonder invloed van zwaartekracht of externe krachten.
Aan de linkerkant van de doos wordt een foton uitgezonden dat naar rechts beweegt. Door impulsbehoud beweegt de doos een klein beetje naar links. Wanneer het foton de rechterwand bereikt, draagt het zijn volledige impuls over aan de doos, waardoor de doos stopt met bewegen.
Het foton heeft zich verplaatst, en de doos heeft zich ook verplaatst, maar er zijn geen externe krachten aanwezig. Daarom moet het massamiddelpunt van het totale systeem constant blijven.
Relativistische energie van het foton
Uit Appendix 9.6 (vergelijking (2)) weten we:
\[ E^{2} = p^{2} c^{2} + m_{0}^{2} c^{4}. \]
Voor een foton geldt \(m_{0} = 0\), dus:
\[ E = pc. \]
De impuls van het foton is dus: \[ p_{\text{photon}} = \frac{E}{c}. \]
Impuls van de doos
De doos met massa \(M\) beweegt een klein beetje naar links met snelheid \(v\). De impuls van de doos is:
\[ p_{\text{box}} = M v. \]
In de tijd \(\Delta t\) die het foton nodig heeft om de rechterkant te bereiken, verplaatst de doos zich over een afstand \(\Delta x\). De snelheid van de doos is:
\[ v = -\frac{\Delta x}{\Delta t}. \]
Vanwege impulsbehoud: \[ p_{\text{photon}} + p_{\text{box}} = 0 \quad\Rightarrow\quad p_{\text{box}} = -p_{\text{photon}}. \]
Dus: \[ M \frac{\Delta x}{\Delta t} = \frac{E}{c}. \]
De lengte van de doos is \(L\), dus de tijd die het foton nodig heeft om de andere kant te bereiken is:
\[ \Delta t = \frac{L}{c}. \]
Daarmee: \[ M \Delta x = \frac{E L}{c^{2}}. \]
Massamiddelpunt van het systeem
Stel nu hypothetisch dat het foton een kleine massa \(m\) heeft. Dan kunnen we het massamiddelpunt van het systeem bepalen. Als de positie van de doos \(x_{1}\) is en de positie van het foton \(x_{2}\), dan is het massamiddelpunt:
\[ \bar{x} = \frac{M x_{1} + m x_{2}}{M + m}. \]
Omdat er geen externe krachten zijn, moet dit massamiddelpunt constant blijven:
\[ \frac{Mx_1+mx_2}{M+m}=\frac{M(x_1-\Delta x)+mL}{M+m} \]Het foton start bij 𝑥2=0, dus krijgen we:
\[ ml=M\Delta x \]Nu krijgen we::
\[ mL=\frac{EL}{c^2} \]Met enige herschikking krijgen we de beroemde relatie:
\[ \boxed{ E = mc^{2}. } \]
Opmerking — nauwkeurige behandeling van het fotonpad
In de oorspronkelijke afleiding wordt aangenomen dat het foton een afstand L aflegt. Maar in werkelijkheid beweegt de doos tijdens de vlucht van het foton een kleine afstand \(\Delta x\) in de tegenovergestelde richting. Het effectieve pad van het foton is daarom:
\[ L\sqrt{1 - \frac{v^{2}}{c^{2}}}\; - \Delta x. \]Dit leidt tot een aangepaste looptijd:
\[ \Delta t = \frac{L\sqrt{1 - \frac{v^{2}}{c^{2}}} - \Delta x}{c}. \]De impulsbalans geeft:
\[ M\,\frac{\Delta x}{\Delta t} = \frac{E}{c} \quad\Rightarrow\quad M\Delta x = \frac{E}{c}\,\Delta t. \]Invullen van \(\Delta t\) geeft:
\[ M\Delta x = \frac{E}{c^{2}} \left( L\sqrt{1 - \frac{v^{2}}{c^{2}}} - \Delta x \right). \]Massamiddelpuntvoorwaarde
Het massamiddelpunt van doos + foton moet constant blijven:
\[ \frac{M x_{1} + m x_{2}}{M + m} = \frac{M(x_{1} - \Delta x) + m\left(L\sqrt{1 - \frac{v^{2}}{c^{2}}} - \Delta x\right)} {M + m}. \]Dit geeft:
\[ -M\Delta x + m\left(L\sqrt{1 - \frac{v^{2}}{c^{2}}} - \Delta x\right) = 0. \]Dus:
\[ m\left(L\sqrt{1 - \frac{v^{2}}{c^{2}}} - \Delta x\right) = M\Delta x. \]Maar eerder vonden we:
\[ M\Delta x = \frac{E}{c^{2}} \left( L\sqrt{1 - \frac{v^{2}}{c^{2}}} - \Delta x \right). \]Daarom:
\[ \frac{E}{c^{2}} \left( L\sqrt{1 - \frac{v^{2}}{c^{2}}} - \Delta x \right) = m\left( L\sqrt{1 - \frac{v^{2}}{c^{2}}} - \Delta x \right). \]De factor tussen haakjes is niet nul, dus:
\[ \boxed{E = m c^{2}}. \]Conclusie
Zelfs wanneer we:
- de verplaatsing van de doos \(\Delta x\) meenemen,
- het verkorte fotonpad gebruiken,
- de Lorentzcontractie meenemen,
komt de afleiding nog steeds exact uit op:
\[ \boxed{E = m c^{2}}. \]Appendix 9.10 — Toepassingen
Appendix 9.10.1 — Kernfusie en Kernsplijting
Wanneer een proton \(p\) en een neutron \(n\) bij elkaar worden gebracht, kunnen zij samensmelten tot een deuteriumkern \(d\). De massa’s van de betrokken deeltjes zijn:
\[ m_{p} = 938.27231\ \text{MeV}/c^{2},\qquad m_{n} = 939.56563\ \text{MeV}/c^{2},\qquad m_{d} = 1875.61339\ \text{MeV}/c^{2}. \]Eenheid: MeV/\(c^{2}\)
Uit de relatie \(E = mc^{2}\) volgt dat massa kan worden uitgedrukt als energie gedeeld door \(c^{2}\). In de deeltjesfysica wordt daarom vaak de elektronvolt (eV) gebruikt:
\[ 1\ \text{eV} = 1.6\times 10^{-19}\ \text{J},\qquad 1\ \text{MeV} = 10^{6}\ \text{eV}. \]De eenheid MeV/\(c^{2}\) is dus een praktische maat voor massa.
Vrijgekomen energie bij fusie
Omdat de massa van het deuteron kleiner is dan de som van de massa’s van proton en neutron, moet er energie zijn vrijgekomen. Als \(p\) en \(n\) met verwaarloosbare snelheid samenkomen:
\[ E = m_{p}c^{2} + m_{n}c^{2} - m_{d}c^{2} = 2.22455\ \text{MeV}. \]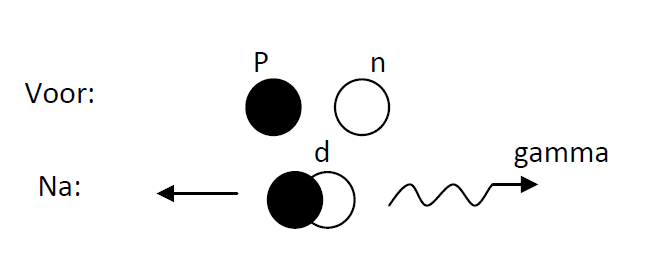
Deze energie komt vrij in de vorm van een foton:
\[ p + n \;\rightarrow\; d + \gamma. \]Een foton is massaloos en draagt energie en impuls. Om impulsconservatie te garanderen beweegt het gevormde deuteron in tegengestelde richting van het foton. Omdat de massa van \(d\) groot is, is de kinetische energie van \(d\) zeer klein:
\[ E = \sqrt{p^{2}c^{2} + m^{2}c^{4}} \approx mc^{2} \qquad\text{als } pc \ll mc^{2}. \]Kernfusie
De hierboven beschreven reactie is een voorbeeld van kernfusie. Lichte kernen kunnen samensmelten tot zwaardere kernen terwijl energie vrijkomt. Alle kernen tot en met ijzer (\(^{56}\text{Fe}\)) kunnen via fusie worden gevormd met netto energieproductie.
Kernsplijting
Voor zeer zware kernen, zoals uranium, geldt het omgekeerde: de totale massa van de kern is groter dan de som van de massa’s van de afzonderlijke nucleonen. Daarom komt er energie vrij wanneer zulke zware kernen worden gesplitst:
kernsplijting (kernfissie).
Dit verklaart waarom:
- fusie energie oplevert voor lichte elementen,
- splijting energie oplevert voor zware elementen.
Appendix 9.10.2 — Elektrische Auto Rijden op 1 gram Waterstof door middel van Kernfusie
We onderzoeken hier hoeveel energie vrijkomt bij kernfusie van waterstof zoals in de zon, waar vier waterstofatomen fuseren tot één heliumatoom. Een klein deel van de massa verdwijnt en wordt omgezet in energie volgens \(E = mc^{2}\). Vervolgens bepalen we hoeveel kilometers een elektrische auto hiermee theoretisch kan rijden.
1. Energieopbrengst van kernfusie
De fusie in de zon verloopt via de proton-protoncyclus. De netto reactie is:
\[ 4\,{}^{1}_1\!H \;\rightarrow\; {}^{4}_2\!He + 2e^{+} + 2\nu_{e} + 2\gamma. \]De massa van vier waterstofatomen is groter dan die van één heliumkern. Het massaverschil komt vrij als energie. Per fusie van vier waterstofatomen komt ongeveer:
\[ 26.7\ \text{MeV} \] vrij.In 1 gram waterstof zitten ongeveer \(6.022\times 10^{23}\)(getal van Avogadro) waterstofatomen (1 mol). Dus, in 1 gram waterstof hebben we \[\frac{6.022 \times 10^{23}}{4}≈1,505 \times 10^{23}\] fusie-reacties.
Elke fusie-reactie geeft 26,7 MeV aan energie, dus totale energie:
\[ E_{\text{fusie}} = 1.505\times 10^{23} \times 26.7\ \text{MeV}. \]2. Omzetten van MeV naar Joule
Een Joule is gelijk het verplaatsen van een lading van 1 Coulomb in een veld van 1 Volt. Dus \[Joule=qV\]
De lading van een elektron e is \(1,60218 \times 10^{−19}\, \text{Coulomb}\).
Dan wordt:
Dus per 1 gram waterstof is de totale energie in Joules:
\[ E_{\text{tot}} = 1.505\times 10^{23} \times 26.7 \times 1.60218\times 10^{-13} \approx 6.43\times 10^{11}\ \text{J}. \]3. Berekening van de energie:
\[ E_{\text{tot}} \approx 6.43\times 10^{11}\ \text{Joules per gram waterstof}. \]
Dit is dus de energie die vrijkomt in dit proces, waarbij dus een klein gedeelte van de massa
wordt omgezet naar energie.
Ter vergelijk kunnen we kijken naar de theoretische berekening wanneer 1 gram materie totaal wordt
omgezet volgens \(E=mc^2\):
\[
E=\frac{1}{1000}\times \left(3\times 10^8\right)^2 \approx 9 \times 10^{13}\, Joules
\]
Dus dit scheelt ongeveer een factor 140 (of in procenten is fusie 0,7% van de energie bij
totale omzetting van 1 gram massa).
4. Alternatieve massadefect-berekening
Bij fusie wordt 4 mol waterstof omgezet in 1 mol helium:
\[ m_{H,4} = 4\times 1.00784 = 4.03136\ \text{g}, \qquad m_{He} = 4.0026\ \text{g}. \]Massaverschil:
\[ \Delta m = 0.02876\ \text{g} = 2.876\times 10^{-5}\ \text{kg}. \]Vrijgekomen energie:
\[ E = \Delta m\,c^{2} = 2.876\times 10^{-5}(3\times 10^{8})^{2} \approx 2.588\times 10^{12}\ \text{J} \] bij 4.03136 g waterstof, dus: \[ E \approx 6.42\times 10^{11}\ \text{J per gram}. \]5. Energieverbruik van een elektrische auto
Elektrische auto's verbruiken gemiddeld:
\[ 17\ \text{kWh per 100 km}. \] \[ 1\ \text{kWh} = 3.6\times 10^{6}\ \text{J}, \qquad 17\ \text{kWh} = 61.2\times 10^{6}\ \text{J per 100 km}. \]6. Theoretische rijafstand (100% efficiëntie)
\[ \text{Afstand} = \frac{6.43\times 10^{11}}{61.2\times 10^{6}} \times 100\ \text{km} \approx 1.05\times 10^{6}\ \text{km}. \]7. Realistische efficiëntie
- Efficiëntie kernfusie → elektriciteit: 40%
- Efficiëntie elektrische aandrijving: 90%
Totale efficiëntie:
\[ \eta = 0.4 \times 0.9 = 0.36. \]Bruikbare energie:
\[ E_{\text{bruikbaar}} = 6.43\times 10^{11} \times 0.36 = 2.31\times 10^{11}\ \text{J}. \]8. Praktische rijafstand
\[ \text{Afstand} = \frac{2.31\times 10^{11}}{61.2\times 10^{6}} \times 100\ \text{km} \approx 3.77\times 10^{5}\ \text{km}. \]Dus een elektrische auto kan theoretisch:
\[ \boxed{ \text{ongeveer } 3.77\times 10^{5}\ \text{km} } \] rijden op de energie uit kernfusie van 1 gram waterstof.Bij een gemiddeld jaarkilometrage van 15.000 km betekent dit:
\[ \frac{3.77\times 10^{5}}{1.5\times 10^{4}} \approx 25\ \text{jaar}. \]Met andere woorden: op 1 gram waterstof kun je ongeveer 25 jaar elektrisch rijden.
Appendix 9.11 — Relativistisch Elektromagnetisme
(Berekeningen gebaseerd op Richard Feynman, Feynman Lectures on Physics, Vol. II, Chapter 13 )
Appendix 9.11.1 — Inleiding
Het woord elektromagnetisme suggereert dat er twee soorten velden bestaan: een elektrisch veld en een magnetisch veld, elk met hun eigen bronnen. In werkelijkheid kennen we slechts één fundamentele bron: de elektrische lading.
Elektrische ladingen — elektronen met lading \(-e\) en protonen met lading \(+e\) — zijn de enige bekende bronnen van het elektrische veld. Tot op heden zijn er geen magnetische monopolen gevonden die als bron van een magnetisch veld zouden kunnen dienen.
Het lijkt er sterk op dat magnetische velden altijd ontstaan door:
- bewegende elektrische ladingen (stroom), of
- tijdvariaties in het elektrische veld.
Zelfs op kwantumschaal zijn magnetische velden het gevolg van elektrische verschijnselen, zoals de spins van elektronen en atomen.
Daarom kan men stellen dat het magnetische veldmodel een buitengewoon nuttig wiskundig hulpmiddel is om elektromagnetische verschijnselen te beschrijven, maar dat het onderliggende fysieke fenomeen volledig elektrisch van aard is: een elektrisch veld en de variatie daarvan in ruimte en tijd.
Appendix 9.11.2 — Berekeningen
Wanneer we een stroomvoerende draad analyseren, gebruiken we normaal gesproken de Maxwell‑vergelijkingen om zowel het elektrische als het magnetische veld te bepalen.
Een alternatieve — en in relativistische context zeer inzichtelijke — benadering is om de volledige berekening uitsluitend op basis van het elektrische veld uit te voeren, en het magnetische veld te beschouwen als een relativistisch bijverschijnsel.
Dit idee vormt de kern van Feynmans behandeling van elektromagnetisme: het magnetische veld is wat een elektrisch veld eruitziet wanneer men het bekijkt vanuit een ander inertiaalstelsel.
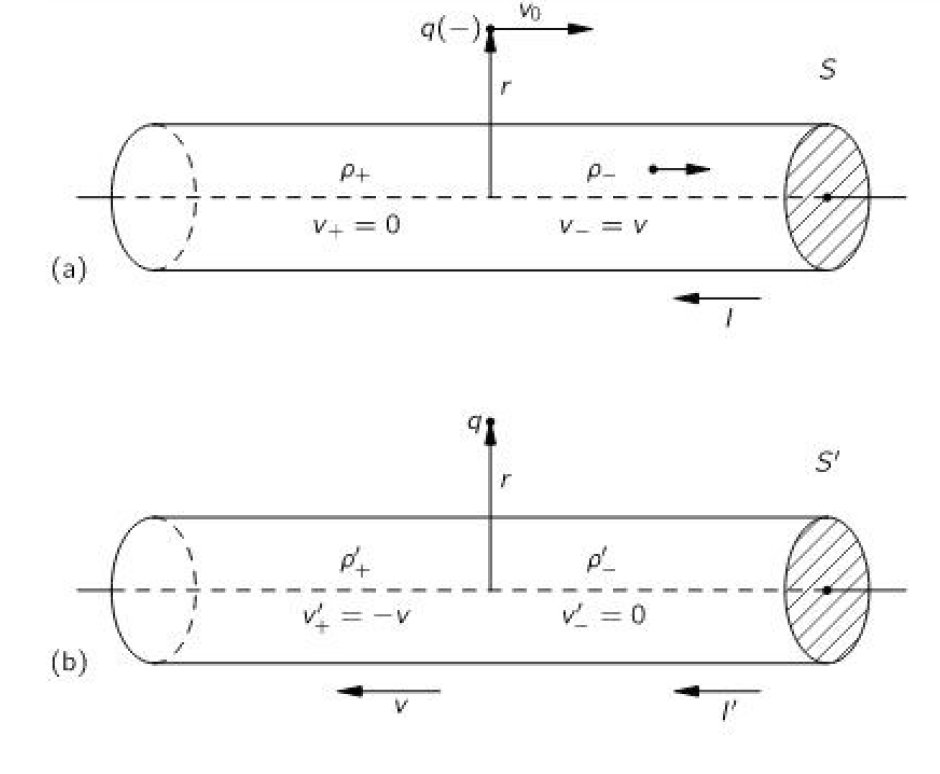
We beschouwen een draad met elektrische stroom en een testlading \(q\). De situatie wordt bekeken in twee verschillende inertiaalstelsels:
- Kader S — de draad is in rust, de lading beweegt.
- Kader S′ — de lading is in rust, de draad beweegt.
Hoewel de fysische situatie dezelfde is, zullen de velden in beide kaders verschillend worden waargenomen. Dit is precies waar relativiteit en elektromagnetisme elkaar ontmoeten.
In de volgende secties zullen we enkele fundamentele formules afleiden die laten zien hoe elektrische velden en ladingsdichtheden transformeren onder Lorentz‑transformaties, en hoe het magnetische veld daaruit automatisch volgt.
Stroomdichtheid en ladingsverdeling
De stroomdichtheid is de gemiddelde stroomsnelheid van de ladingen. Stel dat er een verdeling van ladingen is met een gemiddelde snelheid \(\vec{v}\). De lading \(\Delta q\) die in een tijdsinterval \(\Delta t\) door een oppervlakteelement \(\Delta S\) gaat, is:
\[ \Delta q = \rho\, \vec{v}\cdot\vec{n}\, \Delta S\, \Delta t. \tag{1} \]
Hier is \(\rho\) de ladingsdichtheid: de lading per volume-eenheid. De term \(\vec{v}\Delta t \cdot \Delta S\) kan worden opgevat als een volume. Dus de lading is de ladingsdichtheid maal het volume.
De lading per tijdseenheid is dan: \[ \rho\, \vec{v}\cdot\vec{n}\, \Delta S. \]
Daarom definiëren we de stroomdichtheid:
\[ \boxed{\vec{j} = \rho\, \vec{v}} \tag{2} \]
De totale stroom door een oppervlak \(S\) is:
\[ i = \int_{S} \vec{j}\cdot d\vec{S}. \tag{3} \]
Stroomdrager in rust
We beschouwen nu een draad die in rust is. De elektronen (negatieve ladingen) bewegen met snelheid \(v\) naar rechts. De protonen (positieve ladingen) blijven in rust in de draad.
Een testdeeltje met negatieve lading \(q^{-}\) beweegt met dezelfde snelheid als de elektronen naar rechts. We observeren alles in het stelsel waarin de draad in rust is.
De draad is elektrisch neutraal: \[ \rho_{+} + \rho_{-} = 0. \]
Kracht op het testdeeltje
De kracht op een lading wordt gegeven door de Lorentz‑kracht:
\[ \vec{F} = q(\vec{E} + \vec{v} \times \vec{B}). \]
Het magnetische veld rond een lange rechte draad is:
\[ H = \frac{i}{2\pi r}, \qquad B = \mu_{0} H. \]
Omdat de draad neutraal is, is het elektrische veld buiten de draad nul: \[ \vec{E} = 0. \]
De kracht op het testdeeltje wordt dan:
\[ F = q\, v B \sin\varphi. \]
Aangezien \(\vec{v}\) loodrecht staat op \(\vec{B}\), is \(\sin\varphi = 1\), dus:
\[ F = q v B = q v \mu_{0} H = q v \mu_{0} \frac{i}{2\pi r}. \]
Ladingsdichtheid
De ladingsdichtheid is gedefinieerd als:
\[ \rho = \frac{q}{V}. \]
Als \(A\) de dwarsdoorsnede van de draad is en \(L\) een willekeurige lengte langs de draad, dan is het volume: \[ V = A L, \] en dus: \[ q = \rho A L. \]
Wanneer de draad in rust is, geldt: \[ \rho_{+} + \rho_{-} = 0. \]
Dit vormt de basis voor de relativistische analyse die volgt: in het ene stelsel is de draad neutraal, maar in een ander stelsel — door Lorentzcontractie — verandert de ladingsdichtheid, en ontstaat er een elektrisch veld dat precies overeenkomt met het magnetische effect in het oorspronkelijke stelsel.
Relativistische beschouwing vanuit het perspectief van het testdeeltje
We bekijken nu de situatie vanuit het stelsel waarin het testdeeltje in rust is. In dit stelsel beweegt de draad naar links met snelheid \(v\). Het volume wordt bepaald door de dwarsdoorsnede \(A\) en de lengte \(L\).
De lengte van een bewegend volume ten opzichte van een volume in rust is: \[ L_{\text{moving}} = L_{\text{rest}} \sqrt{1 - \frac{v^{2}}{c^{2}}}. \]
Omdat de elektronen dezelfde snelheid hebben als het testdeeltje, zijn zij in dit stelsel in rust. Dus: \[ L_{\text{rest}} = \frac{L_{\text{moving}}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}. \]
De positieve ionen bewegen nu met snelheid \(v\) naar links. Hun lengte wordt Lorentz‑gecontraheerd met factor: \[ \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}. \]
Nieuwe ladingsdichtheid
In het ruststelsel van de draad was het externe elektrische veld nul: \[ \rho_{+} + \rho_{-} = 0. \]
Maar in het stelsel van het testdeeltje is de bewegende lengte kleiner, dus het bewegende volume kleiner, en dus de ladingsdichtheid groter.
De ladingsdichtheid van de elektronen wordt daarom: \[ \rho_{-}' = \rho_{-} \sqrt{1 - \frac{v^{2}}{c^{2}}}. \]
De positieve ladingsdichtheid wordt: \[ \rho_{+}' = \frac{\rho_{+}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}. \]
De totale ladingsdichtheid is dus: \[ \rho_{\text{netto}} = \rho_{+}' + \rho_{-}' = \frac{\rho_{+}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} + \rho_{-} \sqrt{1 - \frac{v^{2}}{c^{2}}}. \]
Omdat \(\rho_{-} = -\rho_{+}\):
\[ \rho_{\text{netto}} = \rho_{+} \left( \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} - \sqrt{1 - \frac{v^{2}}{c^{2}}} \right). \]
Schrijf dit als: \[ \rho_{\text{netto}} = \rho_{+} \frac{ 1 - \left(1 - \frac{v^{2}}{c^{2}}\right) }{ \sqrt{1 - \frac{v^{2}}{c^{2}}} } = \rho_{+} \frac{\frac{v^{2}}{c^{2}}}{ \sqrt{1 - \frac{v^{2}}{c^{2}}} }. \]
Dus: \[ \boxed{ \rho_{\text{netto}} = \rho_{+}\, \frac{v^{2}/c^{2}}{\sqrt{1 - v^{2}/c^{2}}} } \]
Lading in een lengte \(L\)
Het volume van een lengte \(L\) van de draad is: \[ V = A L. \]
De totale lading in dit volume is: \[ q = \rho_{\text{netto}} A L = \rho_{+}\, \frac{v^{2}/c^{2}}{\sqrt{1 - v^{2}/c^{2}}} A L. \]
Omdat \(\rho_{\text{netto}} \neq 0\), is het elektrische veld buiten de draad niet langer nul. Het staat loodrecht op de draad en gedraagt zich als het veld van een geladen lijn.
Volume van een cilindrische Gauss-oppervlakte
Beschouw een cilindrische buis rond de draad, met:
- lengte \(L\),
- straal \(r\).
Het oppervlak van de mantel is: \[ S = 2\pi r L. \]
Dit zal worden gebruikt om het elektrische veld via de wet van Gauss te bepalen: \[ \oint \vec{E}\cdot d\vec{S} = \frac{q}{\varepsilon_{0}}. \]
In de volgende stap leidt dit tot een elektrisch veld dat exact overeenkomt met de magnetische kracht in het oorspronkelijke stelsel — een prachtig voorbeeld van hoe magnetisme een relativistisch effect is.
Elektrisch veld in het ruststelsel van het testdeeltje
Uit de Gauss‑wet volgt voor het elektrische veld buiten de draad:
\[ E = \frac{\rho_{+}\, v^{2}/c^{2}}{2\pi \varepsilon_{0} rL} \frac{A L}{\sqrt{1 - v^{2}/c^{2}}} = \frac{\rho_{+} v^{2}}{2\pi \varepsilon_{0} r c^{2}} \frac{1}{\sqrt{1 - v^{2}/c^{2}}}A \]
Dus de kracht op het testdeeltje in dit stelsel is:
\[ F' = qE = q\, \frac{\rho_{+} v^{2}}{2\pi \varepsilon_{0} r c^{2}} \frac{A}{\sqrt{1 - v^{2}/c^{2}}}. \tag{4} \]
Voor \(v \ll c\) wordt dit:
\[ F' \approx q\, \frac{\rho_{+}}{2\pi \varepsilon_{0} r} \frac{v^{2}}{c^{2}} A. \]
Kracht in het oorspronkelijke stelsel (magnetisch)
In het ruststelsel van de draad was de kracht:
\[ F = q v B = q v \mu_{0} H = q v \mu_{0} \frac{i}{2\pi r}. \tag{5} \]
Omdat de stroomdichtheid: \[ J = \rho v, \] krijgen we:
\[ F = q v \mu_{0} \frac{J A}{2\pi r} = q v \mu_{0} \frac{\rho v A}{2\pi r}. \]
Gebruik nu: \[ c^{2} = \frac{1}{\varepsilon_{0}\mu_{0}} \quad\Rightarrow\quad \mu_{0} = \frac{1}{\varepsilon_{0} c^{2}}, \] dus:
\[ F = q\, \frac{\rho v^{2} A}{2\pi r\, \varepsilon_{0} c^{2}}. \tag{6} \]
Vergelijking van de twee krachten
Uit (4) en (6) volgt:
\[ F' = \frac{F}{\sqrt{1 - v^{2}/c^{2}}}. \]
Of:
\[ \boxed{ F' = \gamma F } \]
Dit is precies wat we verwachten: de kracht in het transversale vlak (y‑richting) transformeert met een factor \(\gamma\).
Impulsvergelijking in beide kaders
De krachten werken uitsluitend in de transversale y‑richting. Daarom moet de verandering van impuls in de y‑richting in beide kaders gelijk zijn.
In het oorspronkelijke stelsel: \[ \Delta p_{y} = F\, \Delta t. \]
In het stelsel van het testdeeltje: \[ \Delta p'_{y} = F'\, \Delta t'. \]
Omdat tijd voor een bewegend deeltje langzamer verloopt: \[ \Delta t' = \frac{\Delta t}{\gamma}. \]
Vervang dit in de impulsvergelijking:
\[ \Delta p'_{y} = F' \Delta t' = \gamma F \cdot \frac{\Delta t}{\gamma} = F \Delta t = \Delta p_{y}. \]
Dus: \[ \boxed{ \Delta p'_{y} = \Delta p_{y} } \]
Dit bevestigt dat de transversale impuls invariant is onder Lorentz‑transformatie.
En daarmee zien we opnieuw dat het magnetische veld in het ene stelsel niets anders is dan een elektrisch veld in een ander stelsel — een van de mooiste resultaten van de speciale relativiteitstheorie.
Relatie tussen krachten in beide kaders
Uit de tijdsdilatatie volgt:
\[ \Delta t = \frac{\Delta t'}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}. \]
De impulsverandering in beide kaders is: \[ \Delta p_{y} = F\, \Delta t, \qquad \Delta p'_{y} = F'\, \Delta t'. \]
Omdat de transversale impuls invariant is: \[ \Delta p_{y} = \Delta p'_{y}, \] dus:
\[ F\, \Delta t = F'\, \Delta t' = F'\, \Delta t \sqrt{1 - \frac{v^{2}}{c^{2}}}. \]
Daaruit volgt: \[ F' = \frac{F}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}. \tag{7} \]
Met de resultaten uit (5) en (6) krijgen we:
\[ F = q v B = \sqrt{1 - \frac{v^{2}}{c^{2}}}\, F' = \sqrt{1 - \frac{v^{2}}{c^{2}}}\, q E. \]
Of: \[ \boxed{ q v B = \sqrt{1 - \frac{v^{2}}{c^{2}}}\, q E } \]
Dit is precies de relativistische relatie tussen elektrische en magnetische krachten.
Appendix 9.11.3 — Conclusie
We hebben gevonden dat we hetzelfde fysieke resultaat krijgen, ongeacht of we de beweging van een deeltje langs een stroomdraad analyseren in:
- een coördinatensysteem dat in rust is ten opzichte van de draad, of
- een systeem dat in rust is ten opzichte van het deeltje.
In het eerste geval was de kracht volledig magnetisch. In het tweede geval was de kracht volledig elektrisch.
Omdat beide beschrijvingen tot exact dezelfde impulsverandering leiden, moeten elektrische en magnetische velden manifestaties zijn van één en hetzelfde onderliggende relativistische veld.
Dit toont aan dat:
\[ \boxed{ \text{Magnetisme is een relativistisch effect van elektriciteit.} } \]
Dit is een van de mooiste en diepste inzichten van de speciale relativiteitstheorie, en vormt de basis voor de tensorformulering van het elektromagnetische veld.