Appendix 10 — Specifiek Hoekmoment
In dit document, en vooral waar we de Schwarzschild‑vergelijking gebruiken, wordt de term hoekmoment gebruikt in de vorm:
\[ L = m r^{2}\frac{d\phi}{dt}. \]
Omdat: \[ L = m v r = m r v = m r \left(r\frac{d\phi}{dt}\right) = m r^{2}\frac{d\phi}{dt}, \] lijkt dit op het klassieke hoekmoment.
Het is echter niet het werkelijke tweelichamen‑hoekmoment, maar een benadering. Hier volgt de toelichting.
Het tweelichamenprobleem
In de Schwarzschild‑formule beschouwen we een deeltje dat beweegt in het zwaartekrachtsveld van een groot massief lichaam. Het referentiekader is het centrum van dat grote lichaam. Dit is in feite een tweelichamenprobleem.
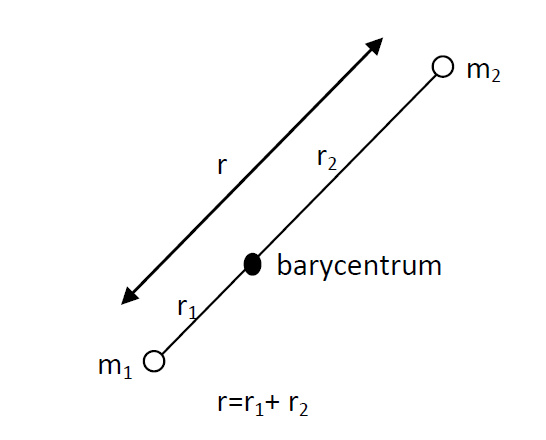
De twee lichamen draaien om hun gemeenschappelijk zwaartepunt (barycentrum). Voor cirkelvormige banen geldt:
\[ m_{1}\frac{v_{1}^{2}}{r_{1}} = m_{2}\frac{v_{2}^{2}}{r_{2}}. \tag{1} \]
Omdat de periodes gelijk moeten zijn:
\[ T = \frac{2\pi r_{1}}{v_{1}} = \frac{2\pi r_{2}}{v_{2}} \quad\Rightarrow\quad \frac{v_{1}}{v_{2}} = \frac{r_{1}}{r_{2}}. \tag{2} \]
Daaruit volgt:
\[ v_{1} = \frac{r_{1}}{r_{2}} v_{2} = \frac{r_{1}}{r_{2}}(v - v_{1}), \tag{3} \]
dus: \[ v_{1} = \frac{r_{1}}{r} v, \qquad v_{2} = \frac{r_{2}}{r} v, \tag{4–5} \] waarbij \(r = r_{1} + r_{2}\).
De relatieve snelheid is: \[ v = v_{1} + v_{2}. \tag{6} \]
Relatie tussen massa’s en afstanden
Vul (3) in in (1):
\[ \frac{m_1v^2_1}{r_1}=\frac{m_1v^2_2}{r_1}\left(\frac{r_1}{r_2}\right)^2=\frac{m_2v^2_2}{r_2} \Rightarrow \frac{m_1}{r_1}\left(\frac{r_1}{r_2}\right)^2=\frac{m_2}{r_2} \]\[\Rightarrow m_{1} r_{1} = m_{2} r_{2}. \tag{7} \]
Hieruit volgt:
\[ r_{2} = \frac{m_{1}}{m_{1} + m_{2}}\, r, \qquad r_{1} = \frac{m_{2}}{m_{1} + m_{2}}\, r. \tag{8} \]
Hoekmoment van beide lichamen
Het hoekmoment van \(m_{2}\) t.o.v. \(m_{1}\):
\[ L_{2} = m_{2} v_{2} r_{2} =m^2\frac{r_2}{r}v\frac{m_1}{m_1+m_2}r_2v = m_{2}\frac{m_{1}}{m_{1}+m_{2}} r_2v =m_2\left(\frac{m_1}{m_1+m_2}\right)^2vr \tag{9} \]
In termen van de hoeksnelheid \(\omega = v/r\):
\[ L_{2} = \frac{1}{m_2}\left(\frac{m_{1} m_{2}}{m_{1}+m_{2}}\right)^2\, \omega r^{2} \tag{10} \]
Op dezelfde manier: \[ L_{1} = \frac{1}{m_1}\left(\frac{m_{1} m_{2}}{m_{1}+m_{2}}\right)^2\, \omega r^{2} \tag{11} \]
Het totale hoekmoment is dus:
\[ L = L_{1} + L_{2} = \frac{m_{1} m_{2}}{m_{1}+m_{2}}\, \omega r^{2}. \]
Of in Schwarzschild‑vorm: \[ L = \frac{m_{1} m_{2}}{m_{1}+m_{2}}\, r^{2}\frac{d\phi}{d\tau}. \tag{12} \]
Gereduceerde massa
We definiëren de gereduceerde massa:
\[ m = \frac{m_{1} m_{2}}{m_{1} + m_{2}}. \tag{13} \]
Het specifieke hoekmoment is dan:
\[ h = \frac{L}{m} = r^{2}\frac{d\phi}{d\tau}. \tag{14} \]
Limiet van een zeer grote centrale massa
Als \(m_{1} = M\) een zeer grote massa is (bijv. een ster of zwart gat) en \(m_{2}\) een klein deeltje:
\[ m = \frac{m_{2} M}{M + m_{2}} \approx m_{2}. \tag{15} \]
Dus wanneer \(M \gg m_{2}\), wordt het hoekmoment bepaald door de massa van het deeltje alleen. Dit rechtvaardigt de gebruikelijke Schwarzschild‑vorm:
\[ L = m r^{2}\frac{d\phi}{d\tau}. \]
Het specifieke hoekmoment: \[ h = r^{2}\frac{d\phi}{d\tau} \] is dan exact de juiste grootheid om in de Schwarzschild‑vergelijking te gebruiken.