Appendix 6 — Afleiding van de Stelling van Gauss

We beginnen met een kubus van infinitesimaal kleine afmetingen.

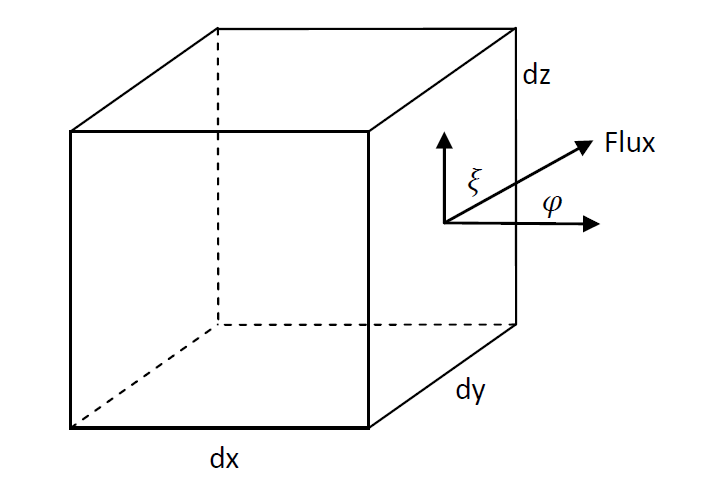
De flux is een vector, omdat deze zowel een grootte als een richting heeft:

\[ \vec{F}_{\text{flux}} = \vec{F}(x,y,z,t) \tag{1} \]

Flux door een oppervlak

Beschouw nu de rechterzijde van de kubus, een vlak evenwijdig aan het \(y\)-\(z\)-vlak. De flux die door dit oppervlak stroomt, wordt bepaald door de component van \(\vec{F}\) die loodrecht op dat vlak staat.

Als \(\xi\) de hoek is tussen \(\vec{F}\) en het oppervlak, dan geldt:

\[ \vec{F}_{\text{rechts}} = \vec{F} \,\sin\xi \, dy\,dz \tag{2} \]

We representeren het oppervlak als een vector \(d\vec{A}\), die loodrecht op het vlak staat:

\[ d\vec{A} = \vec{dy} \times \vec{dz}, \qquad |dA| = \sin\xi \, dy\,dz \tag{3} \]

De flux door de rechterzijde wordt dan:

\[ \vec{F}_{\text{rechts}} = \vec{F} \sin\xi \, dy\,dz = \vec{F} \cos\!\left(\tfrac{\pi}{2}-\xi\right) dA = \vec{F} \cos\varphi \, dA = \vec{F}\cdot d\vec{A} \tag{4} \]

Hierbij staat \(d\vec{A}\) loodrecht op het oppervlak en is \(\varphi\) de complementaire hoek van \(\xi\). We herkennen dus het inwendig product:

\[ Flux_{rechts}=\vec{F}d\vec{A}\,\cos\phi=\vec{F}\cdot d\vec{A} \tag{5} \]

Flux door het totale oppervlak van de kubus

Voor een eindige kubus is de totale flux de som van de bijdragen van alle zes vlakken:

\[ F_{\text{kubus}} = \sum_{\text{alle vlakken}} \vec{F}\cdot d\vec{A} \tag{6} \]

Dit schrijven we als één integraal over het gesloten oppervlak:

\[ F_{\text{kubus}} = \oint_{\partial V} \vec{F}\cdot d\vec{A} \tag{7} \]

Alternatieve benadering: flux als limiet

In de \(x\)-richting is de inkomende flux:

\[ F_{\text{links}} = F_x \, dy\,dz \tag{8} \]

De flux die de rechterzijde verlaat is:

\[ F_{\text{rechts}} = (F_x + dF_x)\, dy\,dz \tag{9} \]

De netto flux in de \(x\)-richting:

\[ F_x^{\text{netto}} = F_{\text{rechts}} - F_{\text{links}} = dF_x\, dy\,dz \tag{10} \]

Analoog:

\[ F_y^{\text{netto}} = dF_y\, dx\,dz, \qquad F_z^{\text{netto}} = dF_z\, dx\,dy \tag{11–12} \]

De totale flux door de kubus:

\[ F_{\text{kubus}} = dF_x\,dy\,dz + dF_y\,dx\,dz + dF_z\,dx\,dy \tag{13} \]

Herschreven met partiële afgeleiden:

\[ F_{\text{kubus}} = \left( \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} \right) dx\,dy\,dz \]

\[ F_{\text{kubus}} = (\vec{\nabla}\cdot\vec{F})\, dV \tag{15} \]

De operator ∇

\[ \vec{\nabla} = \frac{\partial}{\partial x}\,\hat{e}_x + \frac{\partial}{\partial y}\,\hat{e}_y + \frac{\partial}{\partial z}\,\hat{e}_z = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right) \tag{14} \]

Daarmee wordt vergelijking (13):

\[ F_{\text{kubus}} = (\vec{\nabla}\cdot\vec{F})\, dV \tag{15} \]

Netto flux door de kubus

Door te integreren over het volledige volume van de kubus vinden we:

\[ F_{\text{kubus}} = \iiint_{\text{kubus}} (\nabla \cdot \vec{F})\, dV \tag{16} \]

De Stelling van Gauss

Vergelijking (7) gaf de flux door het gesloten oppervlak:

\[ F_{\text{kubus}} = \oint_{\partial V} \vec{F}\cdot d\vec{A} \]

Vergelijking (16) gaf dezelfde flux als volumeterm:

\[ F_{\text{kubus}} = \iiint_V (\vec{\nabla}\cdot\vec{F})\, dV \]

Omdat beide uitdrukkingen dezelfde flux beschrijven, volgt:

\[ \oint_{\partial V} \vec{F}\cdot d\vec{A} = \iiint_V (\vec{\nabla}\cdot\vec{F})\, dV \tag{17} \]

Aangezien het volume willekeurig was (niet noodzakelijk een kubus), geldt dit voor elk gesloten volume:

\[ \oint_{\partial V} \vec{F}\cdot d\vec{A} = \iiint_V (\vec{\nabla}\cdot\vec{F})\, dV \tag{18} \]

Dit is de Stelling van Gauss (ook wel de Divergentiestelling).

Bijzonder geval: nul flux

Indien de netto flux door het gesloten oppervlak nul is:

\[ \oint_{\partial V} \vec{F}\cdot d\vec{A} = 0 \]

dan volgt uit de stelling van Gauss:

\[ \iiint_V (\vec{\nabla}\cdot\vec{F})\, dV = 0 \tag{19} \]

Omdat het volume willekeurig is:

\[ \vec{\nabla}\cdot\vec{F} = 0 \tag{20} \]

Uitgeschreven in componenten:

\[ \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} = 0 \tag{21} \]

In Einstein-notatie (met sommatie over herhaalde index \(\alpha\)):

\[ \frac{\partial F_\alpha}{\partial x_\alpha} = 0 \tag{22} \]