Appendix 12 — Afleiding van de Euler–Lagrange‑vergelijking
Appendix 12.1 — Definitie van de functionaal
We beginnen met een functie \( f_{1} \) die afhangt van drie variabelen: \(t\), \(x_{1}(t)\) en \( \dot{x}_{1}(t) = \frac{dx_{1}}{dt} \):
\[ f_{1} = f\!\left(t,\, x_{1}(t),\, \dot{x}_{1}(t)\right). \tag{1} \]
Hier is \(x_{1}(t)\) een functie van \(t\), dus \(\dot{x}_{1}(t)\) is niet nul. In feite is \(t\) de enige onafhankelijke variabele; \(f_{1}\) is dus een functie van een functie.
We beschouwen nu de functionaal:
\[ I_{1} = \int_{t_{1}}^{t_{2}} f\!\left(t,\, x_{1}(t),\, \dot{x}_{1}(t)\right)\, dt. \tag{2} \]
We zoeken de extremale waarde (minimum, maximum of zadelpunt) van \(I_{1}\). Daarvoor moet gelden:
\[ \delta I_{1} = 0. \tag{3} \]
Appendix 12.2 — Variatie van de baan
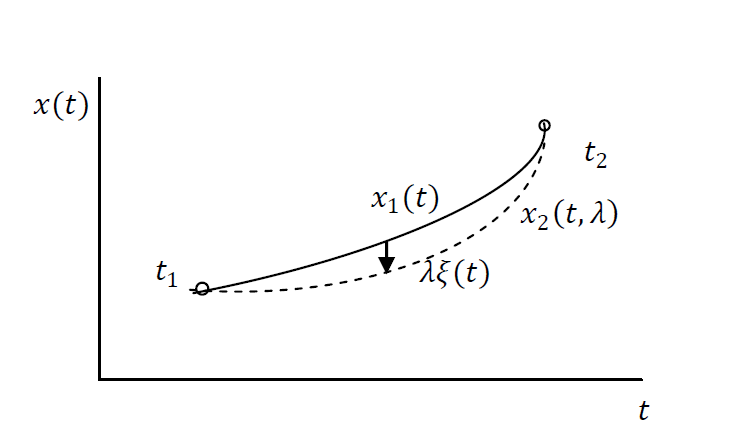
Om te bewijzen dat \(I_{1}\) een extremum is, beschouwen we een licht verschoven curve:
\[ x_{2}(t,\lambda) = x_{1}(t) + \lambda\, \xi(t), \tag{4} \]
waarbij:
- \(\lambda\) een kleine parameter is, onafhankelijk van \(t\),
- \(\xi(t)\) een willekeurige maar gladde functie is.
Omdat de variatie de eindpunten niet mag veranderen, geldt:
\[ \xi(t_{1}) = 0, \qquad \xi(t_{2}) = 0. \tag{5} \]
De functie \(x_{2}(t,\lambda)\) verschilt dus alleen tussen \(t_{1}\) en \(t_{2}\), maar valt samen met \(x_{1}(t)\) op de eindpunten.
Appendix 12.3 — Variatie van de functionaal
De integraal \(I_{2}\) voor de aangrenzende curve is:
\[ I_{2} = \int_{t_{1}}^{t_{2}} f_{2}\, dt. \tag{6} \]
Met: \[ f_{2} = f\!\left(t,\; x_{2}(t,\lambda),\; \dot{x}_{2}(t,\lambda)\right). \]
Door (6) in te vullen in vergelijking (4) krijgen we:
\[ I_{2} = \int_{t_{1}}^{t_{2}} f\!\left( t,\; x_{1}(t) + \lambda \xi(t),\; \dot{x}_{1}(t) + \lambda \dot{\xi}(t) \right)\, dt. \tag{7} \]
Omdat \(I_{1}\) een extreme waarde is, moet ook \(I_{2}\) een extremum zijn voor \(\lambda = 0\):
\[ \lim_{\lambda \to 0} I_{2} = \text{minimum, maximum of zadelpunt}. \tag{8} \]
De extreme waarde wordt gevonden door de afgeleide naar \(\lambda\) te nemen en deze gelijk te stellen aan nul:
\[ \lim_{\lambda \to 0} \frac{d I_{2}}{d\lambda} = 0. \tag{9} \]
In combinatie met vergelijking (6):
\[ \lim_{\lambda \to 0} \frac{d}{d\lambda} \int_{t_{1}}^{t_{2}} f_{2}\, dt = 0, \tag{10} \]
of:
\[ \lim_{\lambda \to 0} \int_{t_{1}}^{t_{2}} \frac{d f_{2}}{d\lambda}\, dt = 0. \]
Appendix 12.4 — Differentiatie naar de variatieparameter
We hadden: \[ \lim_{\lambda \to 0} \frac{d}{d\lambda} \int_{t_{1}}^{t_{2}} f_{2}\, dt = 0. \] Omdat dit een product is van twee functies, passen we de regel van partiële differentiatie toe:
\[ \lim_{\lambda \to 0} \int_{t_{1}}^{t_{2}} \left( \frac{d f_{2}}{d\lambda}\, dt + f_{2}\, \frac{d}{d\lambda}(dt) \right) = 0. \tag{11} \]
Omdat \(t\) en \(\lambda\) onafhankelijk zijn, is: \[ \frac{d t}{d\lambda} = 0, \] dus de tweede term valt weg:
\[ \lim_{\lambda \to 0} \int_{t_{1}}^{t_{2}} \frac{d f_{2}}{d\lambda}\, dt = 0. \tag{12} \]
Appendix 12.5 — Uitwerken van \( \frac{d f_{2}}{d\lambda} \)
We passen nu de kettingregel toe:
\[ \frac{d f_{2}}{d\lambda} = \frac{\partial f_{2}}{\partial t}\frac{dt}{d\lambda} + \frac{\partial f_{2}}{\partial x_{2}}\frac{dx_{2}}{d\lambda} + \frac{\partial f_{2}}{\partial \dot{x}_{2}} \frac{d}{d\lambda}\left(\dot{x}_{2}\right). \tag{13} \]
Omdat \(t\) en \(\lambda\) onafhankelijk zijn, is de eerste term nul:
\[ \frac{\partial f_{2}}{\partial t}\frac{dt}{d\lambda} = 0. \]
Dus: \[ \frac{d f_{2}}{d\lambda} = \frac{\partial f_{2}}{\partial x_{2}}\frac{dx_{2}}{d\lambda} + \frac{\partial f_{2}}{\partial \dot{x}_{2}} \frac{d}{d\lambda}\left(\dot{x}_{2}\right). \tag{14} \]
Omdat: \[ \frac{d}{d\lambda}\left(\dot{x}_{2}\right) = \frac{d}{dt}\left(\frac{dx_{2}}{d\lambda}\right), \tag{15} \] krijgen we:
\[ \frac{d f_{2}}{d\lambda} = \frac{\partial f_{2}}{\partial x_{2}}\frac{dx_{2}}{d\lambda} + \frac{\partial f_{2}}{\partial \dot{x}_{2}} \frac{d}{dt}\left(\frac{dx_{2}}{d\lambda}\right). \tag{16} \]
Appendix 12.6 — Integreren per delen
We integreren nu de tweede term:
\[ \int_{t_{1}}^{t_{2}} \frac{\partial f_{2}}{\partial \dot{x}_{2}} \frac{d}{dt}\left(\frac{dx_{2}}{d\lambda}\right)\, dt = \left[ \frac{\partial f_{2}}{\partial \dot{x}_{2}} \frac{dx_{2}}{d\lambda} \right]_{t_{1}}^{t_{2}} - \int_{t_{1}}^{t_{2}} \frac{d}{dt}\left( \frac{\partial f_{2}}{\partial \dot{x}_{2}} \right) \frac{dx_{2}}{d\lambda}\, dt. \tag{17} \]
Omdat de variatie aan de eindpunten nul is: \[ \xi(t_{1}) = \xi(t_{2}) = 0 \quad\Rightarrow\quad \frac{dx_{2}}{d\lambda}\Big|_{t_{1}}^{t_{2}} = 0, \] valt de grenswaarde weg.
We houden dus over: \[ \int_{t_{1}}^{t_{2}} \left[ \frac{\partial f_{2}}{\partial x_{2}} - \frac{d}{dt}\left( \frac{\partial f_{2}}{\partial \dot{x}_{2}} \right) \right] \frac{dx_{2}}{d\lambda}\, dt = 0. \]
Omdat \(\frac{dx_{2}}{d\lambda} = \xi(t)\) willekeurig is, volgt:
\[ \boxed{ \frac{d}{dt}\left(\frac{\partial f}{\partial \dot{x}}\right) - \frac{\partial f}{\partial x} = 0 } \]
Dit is de Euler–Lagrange‑vergelijking.
Appendix 12.7 — Afronding van de variatie-afleiding
We hadden uit de integraal per delen:
\[ \left[ \frac{\partial f_{2}}{\partial \dot{x}_{2}} \frac{dx_{2}}{d\lambda} \right]_{t_{1}}^{t_{2}} - \int_{t_{1}}^{t_{2}} \frac{dx_{2}}{d\lambda} \frac{d}{dt} \left( \frac{\partial f_{2}}{\partial \dot{x}_{2}} \right) dt. \]
De afgeleide van \(x_{2}\) naar \(\lambda\) volgt uit differentiatie van vergelijking (4):
\[ \frac{dx_{2}(t,\lambda)}{d\lambda} = \frac{d}{d\lambda}\left(x_{1}(t) + \lambda\,\xi(t)\right) = \xi(t). \tag{18} \]
Omdat \(\xi(t_{1}) = \xi(t_{2}) = 0\), verdwijnt de grensbijdrage:
\[ \left[ \frac{\partial f_{2}}{\partial \dot{x}_{2}} \frac{dx_{2}}{d\lambda} \right]_{t_{1}}^{t_{2}} = 0. \]
Daarmee wordt vergelijking (17):
\[ \int_{t_{1}}^{t_{2}} \frac{\partial f_{2}}{\partial \dot{x}_{2}} \frac{d}{dt}\left(\frac{dx_{2}}{d\lambda}\right) dt = - \int_{t_{1}}^{t_{2}} \frac{dx_{2}}{d\lambda} \frac{d}{dt} \left( \frac{\partial f_{2}}{\partial \dot{x}_{2}} \right) dt. \tag{19} \]
Gecombineerd met vergelijking (16) krijgen we:
\[ \int_{t_{1}}^{t_{2}} \left[ \frac{\partial f_{2}}{\partial x_{2}} \frac{dx_{2}}{d\lambda} - \frac{dx_{2}}{d\lambda} \frac{d}{dt} \left( \frac{\partial f_{2}}{\partial \dot{x}_{2}} \right) \right] dt = 0. \tag{20} \]
Omdat \(\frac{dx_{2}}{d\lambda} = \xi(t)\) willekeurig is, volgt dat de integrand nul moet zijn:
\[ \frac{\partial f_{2}}{\partial x_{2}} - \frac{d}{dt} \left( \frac{\partial f_{2}}{\partial \dot{x}_{2}} \right) = 0. \]
Voor \(\lambda = 0\) is \(f_{2} = f_{1}\), dus:
\[ \boxed{ \frac{\partial f_{1}}{\partial x_{1}} - \frac{d}{dt} \left( \frac{\partial f_{1}}{\partial \dot{x}_{1}} \right) = 0 } \tag{21} \]
Hiermee is \(\lambda\) volledig verdwenen en hebben we de algemene voorwaarde gevonden waar een functie aan moet voldoen zodat de integraal \[ I = \int_{t_{1}}^{t_{2}} f(t, x, \dot{x})\, dt \] een extreme waarde heeft.
Dit is de Euler–Lagrange‑vergelijking — het fundament van de klassieke mechanica, veldentheorie en de algemene relativiteitstheorie.
Appendix 12.8 — Algemene vorm van de Euler–Lagrange‑vergelijking
We zijn begonnen met vergelijking (1), waarin de functie slechts afhing van één variabele \(x_{1}(t)\) en zijn afgeleide. We kunnen dit echter veel algemener formuleren door een functie te nemen die afhangt van meerdere functies \(x_{1}(t), x_{2}(t), \ldots, x_{n}(t)\) en hun tijdsafgeleiden:
\[ f_{1} = f\!\left( t,\; x_{1}(t),\, \dot{x}_{1}(t),\; x_{2}(t),\, \dot{x}_{2}(t),\; \ldots,\; x_{n}(t),\, \dot{x}_{n}(t) \right). \tag{22} \]
Voor elk van deze functies volgt dan een Euler–Lagrange‑vergelijking. De algemene vorm van vergelijking (21) wordt:
\[ \frac{\partial f}{\partial x_{n}} - \frac{d}{dt} \left( \frac{\partial f}{\partial \dot{x}_{n}} \right) = 0. \tag{23} \]
Of in een compactere notatie:
\[ \boxed{ \frac{d}{dt} \left( \frac{\partial f}{\partial \dot{x}_{n}} \right) = \frac{\partial f}{\partial x_{n}} } \tag{24} \]
Vergelijking (24) is de Euler–Lagrange‑vergelijking. Zij geeft de noodzakelijke voorwaarde waaraan een functie moet voldoen zodat de integraal
\[ I = \int_{t_{1}}^{t_{2}} f\!\left(t, x_{i}(t), \dot{x}_{i}(t)\right)\, dt \]
een extreme waarde heeft (minimum, maximum of zadelpunt).
Dit vormt het fundament van de variatierekening, de klassieke mechanica, de veldentheorie en de algemene relativiteitstheorie.