Appendix 11 — Overwegingen over Rotatie
Appendix 11.1 — Inleiding
In deze appendix geven we een toelichting op de centrifugale en centripetale kracht, eerst gebaseerd op de klassieke mechanica van Newton, en later breiden we dit uit naar de algemene relativiteitstheorie.
De centrifugale kracht is de schijnbare kracht die van het rotatiecentrum naar buiten werkt. De centripetale kracht is de werkelijke kracht die naar het centrum gericht is en nodig is om een deeltje in een cirkelbaan te houden.
Appendix 11.2 — Impuls
Volgens Newton heeft een bewegend deeltje met massa \(m\) en snelheid \(v\) een impuls:
\[ \vec{p} = m\vec{v}. \]
Als er geen krachten op het deeltje werken, beweegt het uniform in een rechte lijn. Ten opzichte van een punt op afstand \(r\) heeft het deeltje een impulsmoment:
\[ \vec{L} = \vec{r} \times \vec{p}. \]
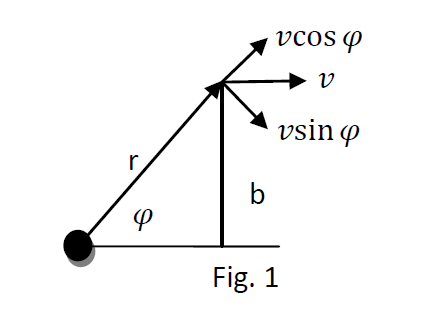
In de bovenstaande afbeelding is het impulsmoment:
\[ L = m v r \sin\varphi = m v b, \]
waarbij \(b = r\sin\varphi\) de loodrechte afstand is tussen de baan van het deeltje en het referentiepunt.
Appendix 11.3 — Cirkelbeweging
Zoals eerder gezegd zal een deeltje uniform in een rechte lijn bewegen als er geen kracht werkt. Dus als de baan van het deeltje een cirkel is, moet er een kracht aanwezig zijn: de centripetale kracht.
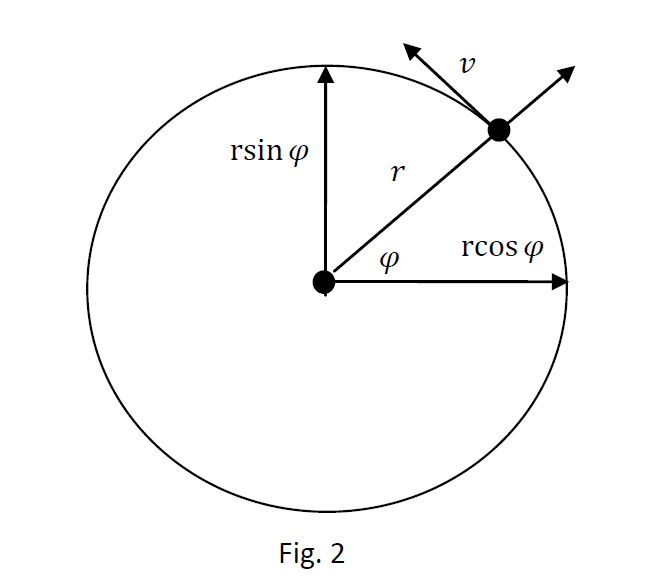
We beginnen met een constante straal \(r\) en splitsen de beweging op in de x‑ en y‑componenten. De positie als functie van de tijd is:
\[ x(t) = r\cos\varphi = r\cos(\omega t), \] \[ y(t) = r\sin\varphi = r\sin(\omega t), \]
waarbij \(\omega\) de hoeksnelheid is.
Snelheden
\[ v_{x} = \frac{dx}{dt} = -\omega r \sin(\omega t), \qquad v_{y} = \frac{dy}{dt} = \omega r \cos(\omega t). \]Versnellingen
\[ a_{x} = \frac{d^{2}x}{dt^{2}} = -\omega^{2} r \cos(\omega t), \qquad a_{y} = \frac{d^{2}y}{dt^{2}} = -\omega^{2} r \sin(\omega t). \]De totale versnelling is:
\[ a = \sqrt{a_{x}^{2} + a_{y}^{2}} = \sqrt{\omega^{4} r^{2}(\cos^{2}\omega t + \sin^{2}\omega t)} = \omega^{2} r. \]Omdat beide componenten negatief zijn (gericht naar het centrum), is de vectoriële versnelling:
\[ \vec{a} = -\omega^{2} r\, \hat{r}. \]Kracht
De totale kracht op het deeltje is:
\[ \vec{F} = m\vec{a} = -m\omega^{2} r\, \hat{r}. \]De grootte van de kracht is:
\[ F = m\omega^{2} r. \]Interpretatie
Het deeltje wil volgens de traagheidswet langs een rechte lijn bewegen. Door de cirkelbeweging ontstaat echter een naar buiten gerichte schijnkracht (centrifugaal in het roterende systeem):
\[ F_{\text{uitwendig}} = m\omega^{2} r. \]Om het deeltje op zijn cirkelbaan te houden, moet deze kracht exact worden gecompenseerd door een naar binnen gerichte reactiekracht:
\[ F_{\text{centripetaal}} = -m\omega^{2} r. \]Deze centripetale kracht houdt het deeltje op zijn cirkelbaan.
Appendix 11.4 — Rotatie van een Bol
Appendix 11.5 Relatie tussen Hoekmoment en EnergieSamen met de centripetale kracht resulteert dit in de volgende kracht op een deeltje op een roterende bol:
\[ F_{\text{radiaal}} = \frac{G m M}{r^{2}} - m \omega^{2} r \sin^{2}(\omega t) = m\left( \frac{G M}{r^{2}} - \omega^{2} r \sin^{2}(\omega t) \right). \]
Daarnaast is er een tangentiële kracht richting de evenaar:
\[ F_{\text{tangentiaal}} = m \omega^{2} r \cos(\omega t)\sin(\omega t). \]
Deeltjes voelen dus een krachtcomponent richting de evenaar, waardoor de bol vervormt tot een ellipsoïde. De afstand van het centrum tot het oppervlak is het kleinst bij de polen en het grootst bij de evenaar. Hierdoor verschilt de zwaartekracht per locatie.
De zwaartekracht hangt ook af van de ingesloten massa. Omdat de afstand tot het centrum bij de polen kleiner is, is de ingesloten massa daar kleiner. De zwaartekracht neemt toe door de kleinere afstand, maar af door de kleinere ingesloten massa.
De uiteindelijke vorm is een ellipsoïde waarin deze effecten in evenwicht zijn. Zie ook: Newtonian Gravity — Rotating Bodies .
Appendix 11.5 Relatie tussen Hoekmoment en Energie
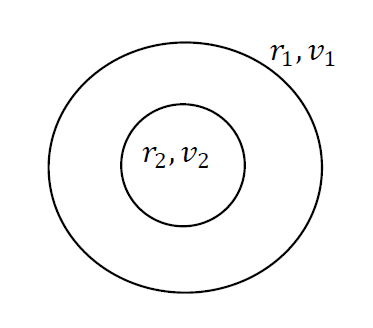
Verschil in kinetische energie tussen twee cirkelbanen
Voor een deeltje dat van een cirkel met straal \(r_{1}\) naar een cirkel met straal \(r_{2}\) beweegt, is het verschil in kinetische energie:
\[ \Delta K = \frac{1}{2}m v_{1}^{2} - \frac{1}{2}m v_{2}^{2}. \tag{1} \]Het hoekmoment is constant:
\[ m v_{1} r_{1} = m v_{2} r_{2} \quad\Rightarrow\quad v_{2} = v_{1}\frac{r_{1}}{r_{2}}. \tag{2} \]Invullen van (2) in (1):
\[ \Delta K = \frac{1}{2}m v_{1}^{2} - \frac{1}{2}m \left( v_{1}\frac{r_{1}}{r_{2}} \right)^{2} = \frac{1}{2}m v_{1}^{2} \left( 1 - \frac{r_{1}^{2}}{r_{2}^{2}} \right). \tag{3} \]Werk geleverd door de centripetale kracht
De centripetale kracht is:
\[ F = -\,m\frac{v^{2}}{r}. \]Het minteken geeft aan dat de kracht naar binnen is gericht. Het werk dat deze kracht verricht wanneer het deeltje van \(r_{1}\) naar \(r_{2}\) beweegt is:
\[ W = \int_{r_{1}}^{r_{2}} F\,dr = \int_{r_{1}}^{r_{2}} \left( -\,m\frac{v^{2}}{r} \right) dr. \]Dit werk moet gelijk zijn aan het verschil in kinetische energie:
\[ W = \Delta K. \]Hiermee is de koppeling gelegd tussen de verandering in kinetische energie en het werk van de centripetale kracht.
Het hoekmoment is constant:
\[ m v r = \text{Const}. \]
Dus: \[ v = \frac{\text{Const}}{m r}. \]
De arbeid verricht door de centripetale kracht tussen \(r_{1}\) en \(r_{2}\) is:
\[ \int_{r_{1}}^{r_{2}} F\, dr = - \int_{r_{1}}^{r_{2}} m \frac{v^{2}}{r}\, dr. \]
Vervang \(v = \frac{\text{Const}}{m r}\):
\[ \int_{r_{1}}^{r_{2}} F\, dr = - \int_{r_{1}}^{r_{2}} m \frac{1}{r} \left( \frac{\text{Const}^{2}}{m^{2} r^{2}} \right) dr = - \int_{r_{1}}^{r_{2}} \frac{\text{Const}^{2}}{m r^{3}}\, dr. \]
Dit geeft:
\[ \int_{r_{1}}^{r_{2}} F\, dr = \frac{\text{Const}^{2}}{2m} \left( \frac{1}{r_{1}^{2}} - \frac{1}{r_{2}^{2}} \right). \]
Omdat: \[ \text{Const} = m v_{1} r_{1}, \] krijgen we:
\[ \frac{\text{Const}^{2}}{2m} = \frac{m^{2} v_{1}^{2} r_{1}^{2}}{2m} = \frac{1}{2} m v_{1}^{2} r_{1}^{2}. \]
Dus: \[ \int_{r_{1}}^{r_{2}} F\, dr = \frac{1}{2} m v_{1}^{2} \left( 1 - \frac{r_{1}^{2}}{r_{2}^{2}} \right). \tag{4} \]
We zien dat formule (3) en (4) gelijk zijn, dus:
\[ \boxed{ \Delta K = \int_{r_{1}}^{r_{2}} F\, dr = \frac{1}{2} m v_{1}^{2} \left( 1 - \frac{r_{1}^{2}}{r_{2}^{2}} \right) } \]
Dit bevestigt dat het verschil in kinetische energie exact overeenkomt met de arbeid van de centripetale kracht — een cruciale stap richting de effectieve potentiaal in centrale krachtsvelden.